其中RL表示导体单位长度的电阻

RDC表示DC单位长度电阻

RAC表示单位长度的电阻系数，与 f的开方成正比

为了深入了解理想有损线路的行为，我们可以从将传输线近似为 n 节 LC 电路开始，添加损耗项并评估电路模型的行为。

在第 7 章中，我们展示了理想的分布式无损传输线可以用等效电路模型来近似，该等效电路模型由具有分流器 C 和串联 L 的集总电路模型部分组成。该模型有时称为传输线的一阶模型、n 节集总电路模型或传输线的无损模型。其一部分如图9-12所示。

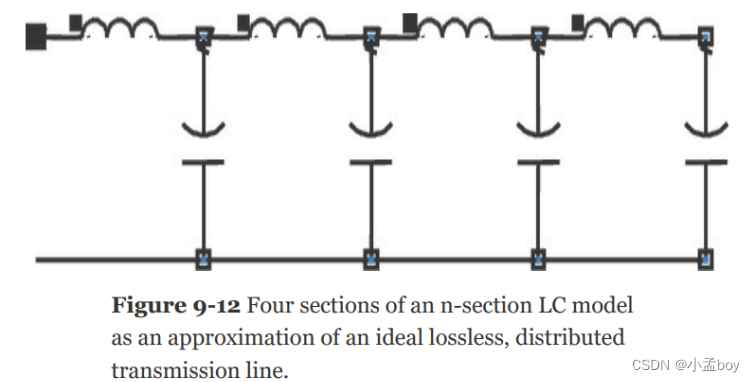
该模型是一个近似值。然而，通过使用足够的部分，它可以是非常准确的近似值，达到非常高的带宽。我们表明，对于时间延迟 TD，实现带宽 BW 所需的最小部分数由下式给出：

n表示一个精准LC模型的节数，BW表示模型的带宽，TD表示传输线的时延

例如，如果模型所需的带宽为2 GHz，线路的时延为1纳秒，物理长度约为6英寸，则精确模型所需的最小节数为n ~ 10 × 2 × 1 = 20。

然而，这种理想的无损模型的一个重大限制是它仍然始终是无损模型。使用这个一阶等效电路模型作为起点，我们可以对其进行修改以考虑损耗。在每个部分中，我们可以添加串联电阻和并联电阻的效果。理想有损传输的 n 节集总电路近似的一小部分将有四个术语来描述它：

C：电容

L：环路自感

Rseries：导体串联电阻

Rshunt：介电损耗分流电阻

如果我们将传输线的长度加倍，则总 C 也会加倍，总 L 也会加倍，总 Rseries 也会加倍。然而，总 Rshunt 减少了一半。如果我们将线路长度加倍，交流漏电流可以流过的面积就会更大，因此分流电阻会减小。

因此，传统上使用漏电电阻的电导而不是电阻来描述它。电导用字母 G 表示，定义为 G = 1/R。根据电阻，电导为：

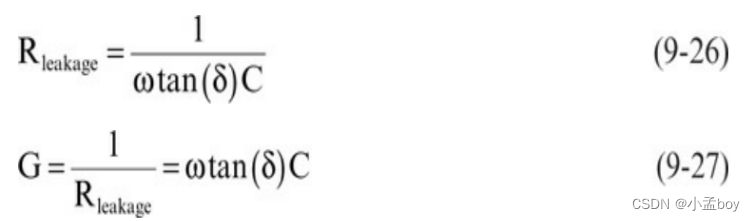
如果传输线的长度加倍，则分流电阻减半，但电导加倍。当我们使用 G 来描述损耗时，我们仍然将损耗建模为电阻随频率而减小的电阻器；我们只是用G参数来描述它。使用电导而不是分流电阻，描述有损传输线的四个术语都与长度成比例。通常是指它们每单位长度的值。这四个术语称为传输线的线路参数：

RL表示导体单位长度的串联电阻

CL表示单位长度电容

LL表示单位长度串联环路电感

GL表示电介质单位长度的分流电导

我们将使用这个理想的二阶 n 段集总电路模型来近似理想的有损传输线，而该传输线又是真实传输线的近似值。图 9-13 显示了等效 nsection RLGC 传输线模型的示例。

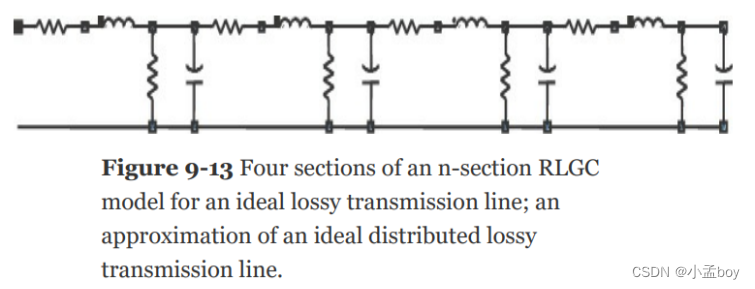
我们使用的部分数量取决于线路的长度和模型的带宽。所需的最小节数仍然大约为 10 × BW × TD。

这是一个等效电路模型。我们可以将电路理论应用于该电路并预测其电气特性。数学很复杂，因为涉及耦合的二阶微分方程，还因为方程很复杂，并且电阻的值随频率变化。求解方程最简单的域是频域。我们假设信号是电压的正弦波，并且可以根据阻抗计算电流的正弦波。仅讨论结果。

在无损线路中，电阻和电导为零。这种无损电路模型将预测传播不失真信号的互连。信号沿途每一步看到的瞬时阻抗等于线路的特征阻抗：

Z0表示特性阻抗，v表示信号速度，CL表示单位长度电容，LL表示单位长度电感。

在此模型中，理想的 L、C 和 Z0 项以及时间延迟均随频率恒定。这些是定义理想无损传输线的唯一术语。从线路一端进入的信号将从另一端退出，幅度没有变化。除了由于可能的阻抗变化而引起的反射之外，对正弦波的唯一影响是传输中的相移。

然而，当将 R 和 G 项添加到模型中时，理想有损传输线的行为与理想无损传输线略有不同。当求解微分方程时，结果相当复杂。该解在频域中不假设 CL 、LL 、RL 或 GL 如何随频率变化。在每个频率，它们可能会改变，也可能是恒定的。

最终的解决方案具有三个重要特征：

1特性阻抗与频率相关且复杂。

2正弦波信号的速度是频率相关的。

3引入了一个新术语，用于描述正弦波沿线路传播时幅度的衰减。这种衰减也与频率相关。

当杂项清除后，特性阻抗、速度和单位长度衰减的精确值由下式给出：

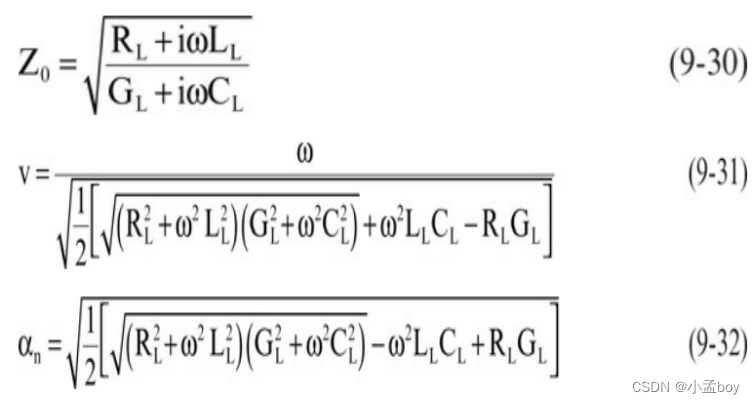
其中：

Z0表示特性阻抗，v表示信号速度，αn表示每长度振幅的衰减，以奈珀斯/长度为单位，ω = 正弦波的角频率，以弧度/秒为单位，RL = 每根导体长度的串联电阻，CL表示单位长度的电容，LL表示单位长度的串联环路电感，GL表示电介质单位长度的分流电导

这些方程非常复杂，尽管可以在电子表格中实现，但很难用来获得有用的工程见解。为了简化代数，通常做出的近似之一是线是有损的，但不是太有损。这称为低损耗近似。近似值是串联电阻 RL 为 RL << ωLL，并联电导 GL 为 GL << ωCL。

该近似假设与导体串联电阻相关的阻抗比与环路电感相关的串联阻抗小。同样，与通过信号和返回路径之间的电容的分流电流相比，通过电介质的漏电阻的分流电流较小。

对于 1 盎司铜走线，约 10 MHz 以上的串联电阻将随频率的平方根增加，并且 ωL 将随频率线性增加。在某些频率下，这种近似会很好，并且在越来越高的频率下会变得更好。

1 盎司铜迹线单位长度的直流电阻为：

RL表示单位长度电容，w表示线宽。

高于 10 MHz 时，电流将在更薄的横截面中流动，趋肤深度将决定电流分布的厚度，而不是 1 盎司铜的 34 微米几何厚度。铜的集肤深度为：

δ表示趋肤深度，f = 正弦波频率分量，单位 MHz

1 盎司铜走线单位长度的交流电阻（高于约 10 MHz）约为：

RL = 每长度电阻，单位为欧姆/英寸

δ=  趋肤深度

t = 几何厚度，以微米为单位，对于 1 盎司铜 = 34 微米

w = 线宽

f = 正弦波频率分量，单位 MHz

ω = 正弦波频率分量，以弧度/秒为单位

对于 50 欧姆线路，单位长度的电感大约为 9 nH/英寸。当 ωLL >> RL 或： 时，就会出现低损耗状态：

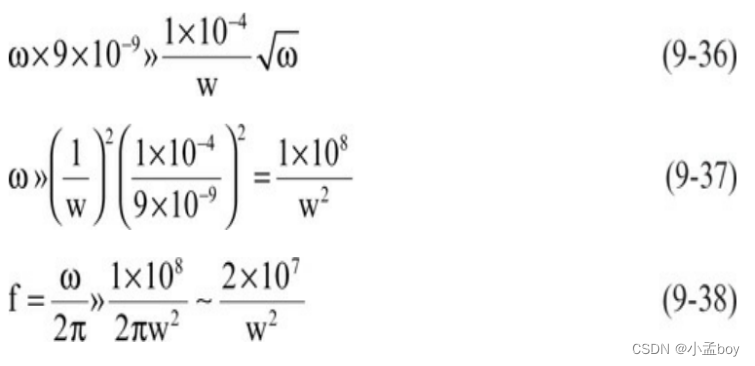
其中：

RL = 每长度电阻，单位为欧姆/英寸

ω = 正弦波频率分量，以弧度/秒为单位

f = 正弦波频率分量，在低损耗状态下以 Hz 为单位

w = 线宽

这是一个令人震惊的结果。结论是，对于宽度超过 3 密耳的线宽，低损耗状态适用于高于 2 MHz 的正弦波频率分量。在这种情况下，串联电阻的阻抗远小于串联电感的电抗。对于宽度超过 3 密耳的线路，低损耗状态从更低的频率开始。非常有损耗的区域实际上是在低频，低于趋肤深度发挥作用的频率。

电导将大致随频率线性增加，而电容将大致随频率恒定。当 GL << ωCL 时，就会出现低损耗状态。这是当 tan(δ) << 1 时。对于几乎所有互连材料，耗散因子都小于 0.02，并且互连始终处于低损耗状态。

具有 3 密耳或更宽迹线的电路板互连的低损耗机制适用于 2 MHz 以上的频率，这是最重要的频率组件所在的位置。

结论是，低损耗近似对于高速数字应用中感兴趣的所有重要频率范围来说是一个非常好的近似。