0. 简介
最近激光SLAM的新工作真的是越来越多了,而大多数当前的激光SLAM系统都是在点云中构建地图,即使在人眼看来是稠密的,但当放大时,点云是稀疏的。稠密地图对于机器人应用至关重要,例如基于地图的导航。由于内存成本低,近年来,网格已成为一种有吸引力的稠密建图模型。《Real-time LiDAR Simultaneous Localization and Meshing》提出了第一个仅使用CPU的实时LiDAR SLAM系统,该系统可以同时构建网格地图并针对网格地图执行定位。采用高斯过程重构的直接网格化策略实现了网格地图的快速构建、配准和更新。具体的开源代码也已经在Github上了。
1. 主要贡献
本文贡献如下:
-
我们提出了一种基于GP重建和顶点连接的网格划分策略,该策略允许快速构建、查询和更新网格地图
-
我们设计了一种点到网格的配准方法。结合约束组合和多线程实现,我们确保了网格地图定位和建图的效率和准确性。
-
我们在网格地图上开发了一个稠密、实时、可扩展的开源LiDAR SLAM系统,并通过实验证明了其优势。

2. 方法概述
本文的动机是在LiDAR SLAM系统中构建、利用和维护一个网格地图。图2展示了一个总体概述。该系统主要由三个组件组成:网格化、配准和网格管理。首先,每个新的LiDAR扫描都使用常速度模型的初始猜测将其转换为世界坐标系{ W W W}下的 S r a w S^{raw} Sraw。以下操作也在{ W W W}中执行。然后,将点分配到体素单元中。GP在每个单元内重建局部表面并获得顶点 v i v_i vi,这些顶点相互连接形成网格。在配准组件中,设计了一种点对网格的配准方法,将重建的当前扫描与构建的网格地图 M M M对齐。最后,网格地图进行迭代更新。
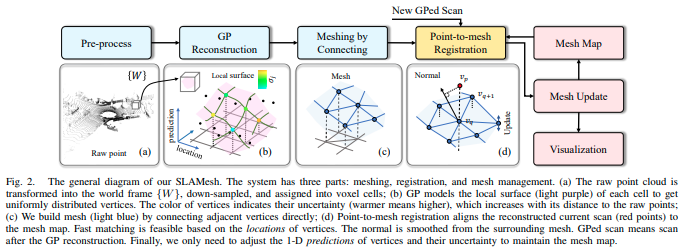
图2. 我们SLAMesh的一般图示。系统分为三个部分:网格化、配准和网格管理。(a)原始点云被转换到世界坐标系{ W W W},进行下采样,并分配到体素单元格中;(b)高斯过程模型(浅紫色)对每个单元格的局部表面进行建模,以获得均匀分布的顶点。顶点的颜色表示它们的不确定性(较暖表示较高),随着其与原始点的距离的增加而增加;©我们通过直接连接相邻顶点来建立网格(浅蓝色);(d)点对网格配准将重建的当前扫描(红点)对齐到网格地图。基于顶点位置的快速匹配是可行的。法线从周围的网格平滑。GPed扫描表示经过高斯过程重建后的扫描。最后,我们只需要调整顶点的1-D预测和它们的不确定性,以维护网格地图。
3. 网格化策略
如前所述,构建和更新网格是耗时的。为了解决这个问题,我们采用了一种重建和连接策略,以便后面的流程可以在实时运行。如图2所示,GP从体素内部的嘈杂和稀疏点云中恢复局部表面。然后,顶点是表面的插值结果。三维顶点的两个坐标均匀分布(称为位置),而另一个坐标(称为预测)具有连续的值域。位置作为索引,以实现快速查询,预测的值域连续,以避免离散化导致的精度损失。
在这里描述了GP过程(更详细的GP描述可以在 [ 16 ] [ 17 ] [16][17] [16][17]中找到)。粗体小写字母表示向量,大写字母表示矩阵。GP的输入是原始点云 S k r a w = { p i = ( x i , y i , z i , σ i n 2 ) , i = 1 , . . . . , n i } S^{raw}_k= \{ p_i = (x_i , y_i , z_i , σ^2_{in}), i = 1, ...., n_i\} Skraw={pi=(xi,yi,zi,σin2),i=1,....,ni}的子集,包含 n i n_i ni个点,其中 k k k表示当前扫描中的第 k k k个单元格 C k C_k Ck, σ i n 2 σ^2_{in} σin2是输入噪声的各向同性方差。输出是一个包含 n j n_j nj个带有不确定性 σ j 2 σ^2_j σj2的顶点 L k z L^z_k Lkz,其中 { v j = ( x j , y j , z j , σ j 2 ), j = 1 , … , n j } \{v_j =(x_j,y_j,z_j,σ^2_j),j = 1,…,n_j\} {vj=(xj,yj,zj,σj2),j=1,…,nj}。上标 z z z表示GP预测坐标 z z z为 f ~ = { z j , j = 1 , … , n j } \tilde{f} = \{z_j,j = 1,…,n_j\} f~={zj,j=1,…,nj},当坐标可以是 x x x, y y y或 z z z中的任何一个时,该上标被省略。我们将输入和输出点集的位置表示为 i i i和 j j j。给定输入观测 f f f,预测$\tilde{f} 也遵循高斯分布。 也遵循高斯分布。 也遵循高斯分布。\tilde{f} $的期望值是:
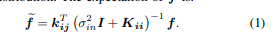
预测的不确定性指的是其方差。
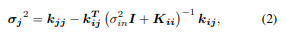
k j j k_{jj} kjj、 k i j k_{ij} kij和 k i i k_{ii} kii分别表示位置核函数的不同组合
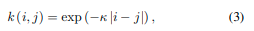
其中 k ( i , j ) k (i, j) k(i,j)是一个比例值, κ κ κ是一个常数(我们算法中 κ = 1 κ=1 κ=1)。这个指数核函数可以表示2D流形中的局部光滑曲面。因此,当建模一个复杂的结构时,一个单元格可以包含更多具有不同高斯过程函数的网格层(如果所有坐标都进行了插值,最多可以有3层)[17]。
在某个阈值 σ m a t c h 2 σ^2_{match} σmatch2下,具有不确定性 σ j 2 σ^2_j σj2 的顶点是足够准确或有效的。三角网格面是通过连接相邻或对角线顶点在位置的2D空间中建立的。如果所有顶点都有效,则网格面有效。与Delaunay三角化类似,在2D空间中建立边缘,我们的方法可以防止薄片网格面。
4. 点对网格配准(重点)
如前所述,我们同时进行定位和网格化,以便网格化可以从定位中受益。为此,一个直观的想法是将顶点视为点或从面中提取点,然后使用传统的点云配准进行姿态估计。然而,这个想法忽略了网格面的法线信息。Puma [3] 表明点对网格的误差可以提高精度。与Puma中的射线投射数据关联不同,我们的SLAMesh是基于位置建立对应关系的。
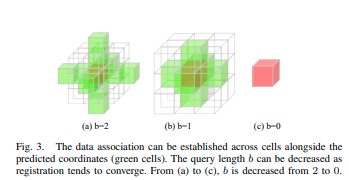
图3。数据关联可以在预测坐标(绿色单元格)旁边的单元格之间建立。随着配准趋于收敛,查询长度 b b b可以减小。从(a)到©, b b b从2减小到0
对于重建的当前扫描 S g p S^{gp} Sgp中的顶点 v p v_p vp,我们首先查询位于相同或相邻单元格中的子网格层(参见图3),然后找到共享相同位置的顶点 v q v_q vq(参见图2(d))。在网格中沿边查找 n q n_q nq个相邻顶点是快速的。包含 v q v_q vq的那些面的法线被平均以获得平滑的法线 n ˉ \bar{n} nˉ,以防表面不光滑。建立 v p v_p vp和包含 v q v_q vq的有效面之间的数据关联:
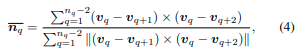
其中 ∣ ∣ ⋅ ∣ ∣ ||·|| ∣∣⋅∣∣是2-范数。我们将一个单元格中的对应数量表示为 n q n_q nq,重叠单元格的数量为 K K K。点 v p ′ v'_p vp′和应用变换 T ∈ S E 3 T∈SE3 T∈SE3(包括旋转 R R R和平移 t t t)后的点到网格的残差。
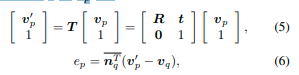
其中上标 T T T表示矩阵转置。最优相对变换 T T T是在优化问题中计算的,其中所有 K K K个重叠层 L k L_k Lk中的点到网格的残差被合并。
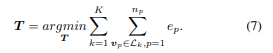
我们使用Ceres solver1中的Levenberg-Marquardt算法来解决这个非线性最小二乘问题。分析雅可比矩阵被导出以加速解决过程。
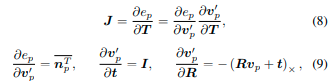
其中符号 ( ⋅ ) × (·)_× (⋅)×表示向量的对应的反对称矩阵。网格可能包含许多面,因此优化问题可能非常大。我们在优化之前通过平均将每个层内的残差合并为一个,以加快优化过程。
将数据存储在体素单元中会在边界上引起数据关联的不连续性。如果我们只在重叠单元上执行配准,当车辆移动速度很快时,配准的收敛区会太窄。因此,我们允许交叉单元重叠,通过查询每个层的预测轴旁边的单元来实现,如图3所示。当配准趋于收敛时,查询的长度会减小。