文章目录

• • • 拆分字符串
    • 三角形最小路径和
    • 不同路径
    • 最小路径和
    • 背包问题

class Solution {
public:
    int fib(int n) {
        // if(n==0)
        // {
        //     return 0;
        // }
        // if(n==1||n==2)
        // {
        //     return 1;
        // }
        // return fib(n-1)+fib(n-2);

        //上面的方法会发现时间复杂度太大，超出时间限制O(2^n)
        /
        //创建一个数组，保留中间状态的解
        
        // int* F=new int[n+2];
        // int MOD = 1000000007;
        // //初始化fib(0),fib(1)
        // F[0]=0;
        // F[1]=1;
        // //创建方程 f(n)=f(n-1)+f(n-2);
        // for(int i=2;i<=n;++i)
        // {
        //     F[i]=(F[i-1]+F[i-2])%MOD;
        // }
        // //返回结果
        // int result=F[n];
        // delete[] F;
        // return result;
        /

        //上面的方法还是可以继续优化的，空间复杂度还可以大幅度优化
        int fib;
        int MOD = 1000000007;
        int fib1=0;
        int fib2=1;
        if(n==0)
        {
            return 0;
        }
        if(n==1)
        {
            return 1;
        }
        for(int i=2;i<=n;i++)
        {
            fib=(fib1+fib2)%MOD;
            fib1=fib2;
            fib2=fib;
        }
        return fib;

    }
};

拆分字符串

class Solution {
public:
    bool wordBreak(string s, unordered_set<string> &dict) {
         int len=s.length();
         vector<bool> dp(len+1,false);
        dp[0]=true;//初始

         for(int i=1;i<=len;i++)
         {
            for(int j=i-1;j>=0;j--)
            {    //利于遍历,它的意义和下面的dp[i]=true是相关联的只有上一个为true,才会出现下一个
         //这也就是为什么在最后取true,就能保证前面的单词也在字典当中，最少是一个整体，因为开始有个true
                if(dp[j]&&dict.find(s.substr(j,i-j))!=dict.end())//公式
                {//注意上面的执行顺序，要确定dict当中有之后才进行的！=比较
                    dp[i]=true;
                    break;
                }
            }
         }
         return dp[len];
    }
};

三角形最小路径和

//第一种写法，是从上往下进行
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param triangle int整型vector<vector<>> 
     * @return int整型
     */
    int minTrace(vector<vector<int> >& triangle) {
        // write code here
        if(triangle.empty())
        {
            return 0;
        }
        int row=triangle.size();//行
        //int col=triangle[0].size();//列
        //这里的列只是求的是第一行的数值，所以就导致最后的遍历需要使用row
        //他是个等腰直角三角形，所以行和列是相等的
        for(int i=1;i<row;i++)
        {   //要注意区分j==0,j==i
            for(int j=0;j<=i;j++)
            {
                if(j==0)
                {
                    triangle[i][j]=triangle[i-1][j]+triangle[i][j];
                }
                else if(j==i)
                {
                    triangle[i][j]=triangle[i-1][j-1]+triangle[i][j];
                }
                else {
                    triangle[i][j]=min(triangle[i-1][j],triangle[i-1][j-1])+triangle[i][j];
                }
            }
        }
        //将每一列的嘴小结果放到最后一行，最后间进行比较

        int mintri=triangle[row-1][0];
        for(int i=1;i<row;i++)
        {
            mintri=min(mintri,triangle[row-1][i]);
        }

        return mintri;
    }
};

//第二种写法，是从下往上进行
class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if(triangle.empty())
        {
            return 0;
        }
        int row=triangle.size();//行
        //int col=triangle[0].size();//列
        //从倒数第二行开始，自下往上
        //在倒数第二行的的情况下进行向下查找较小数值（倒一），到三找倒二较小的值
        for(int i=row-2;i>=0;i--)
        {
            for(int j=0;j<=i;j++)
            {
                triangle[i][j]=min(triangle[i+1][j],triangle[i+1][j+1])+triangle[i][j];
            }
        }

        return triangle[0][0];
    }
};

不同路径

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> f(m, vector<int>(n));
        //先进行初始化只要是在第一行或者第一列上的都进行初始化为1
        for (int i = 0; i < m; ++i) {
            f[i][0] = 1;
        }
        for (int j = 0; j < n; ++j) {
            f[0][j] = 1;
        }
        //f[i][j] = f[i - 1][j] + f[i][j - 1];转移方程
        //因为只能向下或者向右，所以就是 f[i - 1][j] ，f[i][j - 1]这两个位置的和
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                f[i][j] = f[i - 1][j] + f[i][j - 1];
            }
        }
        return f[m - 1][n - 1];
    }
};

最小路径和

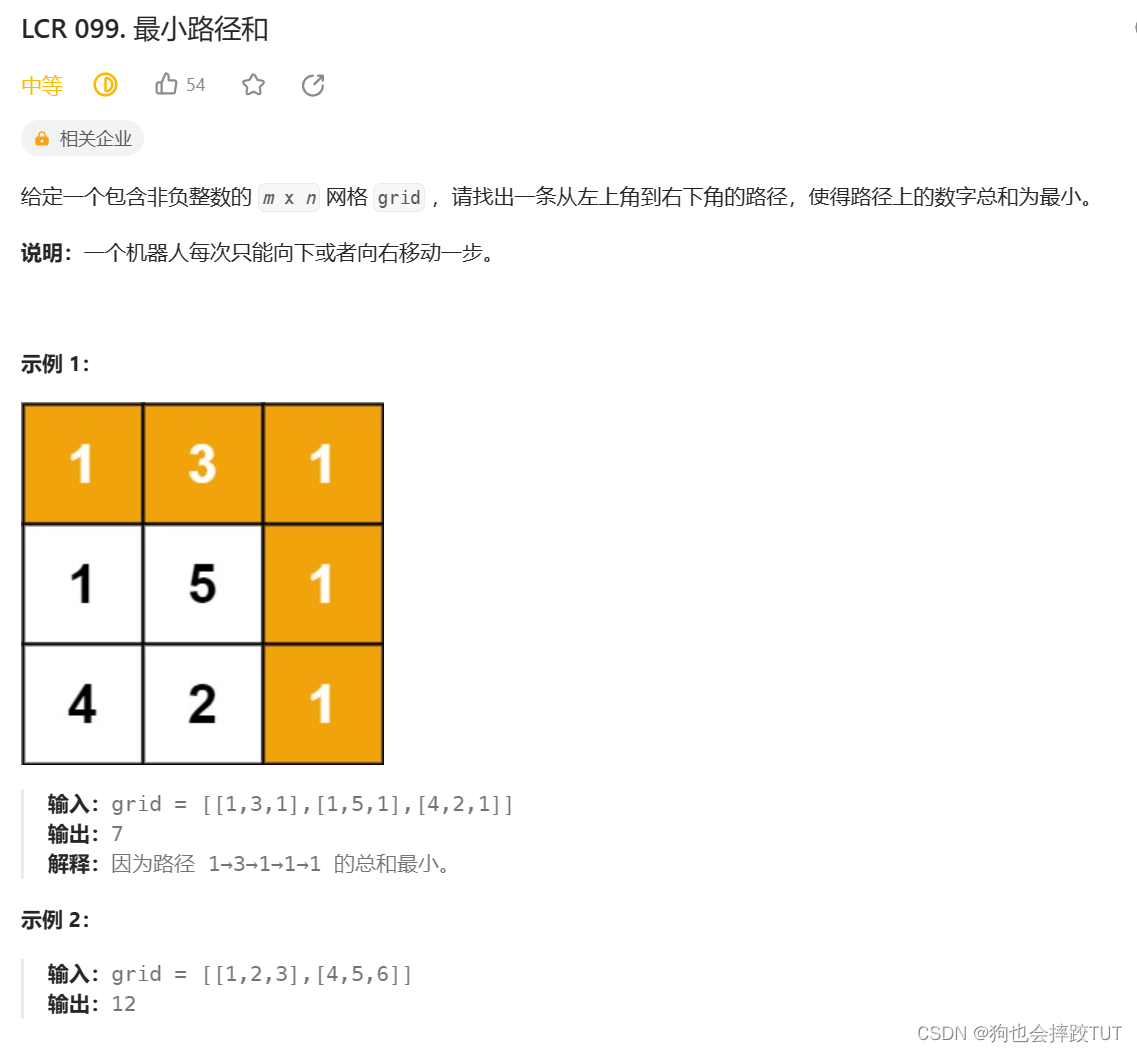
class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
         if (grid.size() == 0 || grid[0].size() == 0) {
            return 0;
        }
        
        int row =grid.size();
        int col=grid[0].size();

        for(int i=1;i<row;i++)
        {
            grid[i][0]+=grid[i-1][0];
        }

        for(int j=1;j<col;j++)
        {
            grid[0][j]+=grid[0][j-1];
        }

        for(int i=1;i<row;i++)
        {
            for(int j=1;j<col;j++)
            {
                grid[i][j]+=min(grid[i-1][j],grid[i][j-1]);
            }
        }

        return grid[row-1][col-1];
    }
};

背包问题

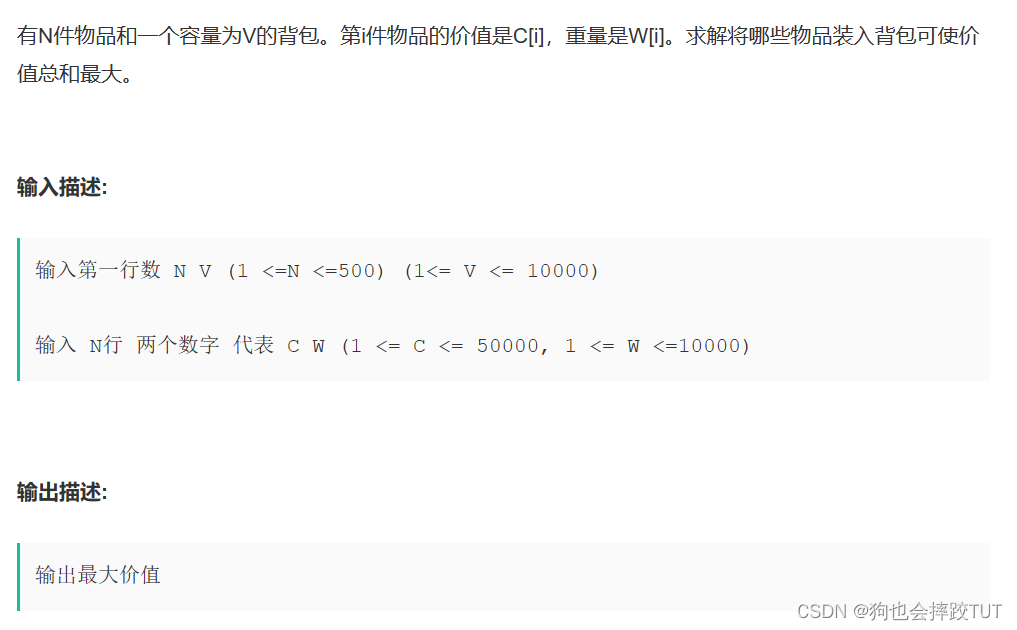
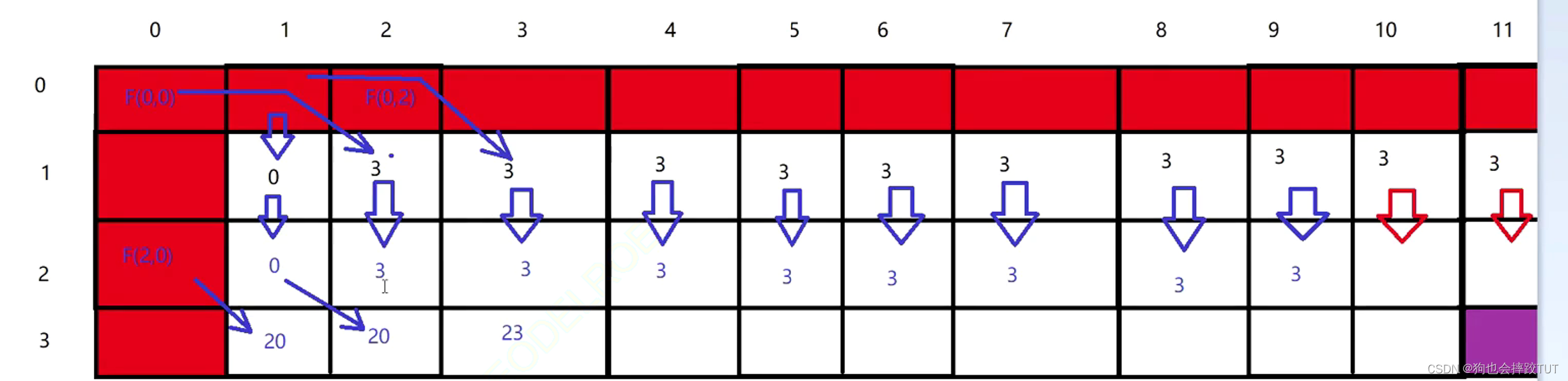
//上面图片的红色部分是用来初始化的，
//int tmp_best = value[i - 1] + dp[i - 1][j - capacity[i - 1]];
//dp[i][j] = max(tmp_best, dp[i - 1][j]);
//通过上面的代码进行比较来判断是否需要继承上一行的值，或者创造出更大的值
#include <iostream>
#include<vector>
using namespace std;

int main() {
    int N, V;
    while (cin >> N >> V) {
        vector<int> value(N);//存储每个物品的价值
        vector<int> capacity(N);//存储每个物品的容量
        for (int i = 0; i < N; ++i) {
            cin >> value[i] >> capacity[i];
        }
        vector<vector<int>> dp(N + 1, vector<int>(V + 1, 0));
        //有N+1行，但是从1开始遍历，所以每行表示每个物品
        //有V+1列，但是从1开始遍历，所以每列表示从1开始到最大容量 的 各种情况下 的 物品最大价值存储
        for (int i = 1; i < N + 1; ++i) {
            for (int j = 1; j < V + 1; ++j) {
                if (capacity[i - 1] > j) { //如果不下，那就等于上次的最优存储
                    //这里的capacity[i-1]是因为这里的i从1开始
                    dp[i][j] = dp[i - 1][j];
                } else //如果能放下，有两种情况：1、放 2、不放
                    //放和不放取决于放了之后是否是最优的，于是创建一个临时变量。
                {
                    //dp[i-1][j-capacity[i-1]]：i-1：上面一行，j-capacity[i-1]：装了i-1这个物品之后还剩的容量。所以整体就是：当前的tmp_best == 装了i-1物品的价值 + 装了这个物品后剩余的容量还可以装的最优的方案
                    int tmp_best = value[i - 1] + dp[i - 1][j - capacity[i - 1]];
                    dp[i][j] = max(tmp_best, dp[i - 1][j]);
                }
            }
        }
        //返回最后一个元素就是最优的方案
        cout << dp[N][V] << endl;
    }
    return 0;
}