一、论文
- 研究领域:机器学习
- 论文:Group Equivariant Convolutional Networks
-
PMLR Proceedings of Machine Learning Research
-
2016
- 论文链接
二、论文简述
三、论文详述
群等变卷积网络
- Abstract
我们引入群等变卷积神经网络(G-CNN),卷积神经网络的自然泛化,通过利用对称性降低样本复杂度。G-CNN使用G卷积,这是一种新型的层,它享有比常规卷积层更高程度的权重共享。G-卷积在不增加参数数量的情况下增加了网络的表达能力。组卷积层易于使用,并且对于由平移、反射和旋转生成的离散组,可以以可忽略的计算开销来实现。G-CNN在CIFAR 10和旋转MNIST上实现了最先进的结果。
- Introduction
深度卷积神经网络(CNN,convnets)已被证明是非常强大的感知数据模型,如图像,视频和音频。虽然目前缺乏强有力的神经网络设计理论,但大量的经验证据支持卷积权重共享和深度(以及其他因素)对于良好的预测性能都很重要。
卷积权重共享是有效的,因为在大多数感知任务中存在平移对称:标签函数和数据分布都近似地不随移位而变化。通过使用相同的权重来分析或建模图像的每个部分,卷积层使用的参数比完全连接的少得多,同时保留了学习许多有用变换的能力。
卷积层可以在深度网络中有效地使用,因为这样的网络中的所有层都是平移等变的:移动图像然后将其馈送通过多个层与将原始图像馈送通过相同的层然后移动所得到的特征图(至少达到边缘效果)相同。换句话说,对称性(平移)由每一层保持,这使得不仅可以在网络的第一层中利用它,而且可以在更高层中利用它。
在本文中,我们展示了如何将卷积网络推广到利用更大的对称性,包括旋转和反射。等方差的概念是这种推广的关键,因此在第2节中,我们将讨论这个概念及其在深度表示学习中的作用。在讨论了第3节中的相关工作之后,我们回顾了第4节中的一些数学概念,这些概念允许我们以通用的方式定义和分析G卷积。在第5节中,我们分析了标准CNN的等变特性,并表明它们对平移是等变的,但可能无法与更一般的变换等变。使用第4节的数学框架,我们可以通过类比标准CNN(后者是翻译组的G-CNN)来定义G-CNN(第6节)。我们证明了G-卷积以及现代CNN中使用的各种层,如池化、任意逐点非线性、批量归一化和残差块都是等变的,因此与G-CNN兼容。在第7节中,我们提供了群卷积的具体实现细节。
在第8节中,我们报告了MNIST-rot和CIFAR 10的实验结果,其中G-CNN实现了最先进的结果(MNIST-rot上的2.28%误差和CIFAR 10上的4.19%误差)。CIFAR 10增强型和普通型为6.46%)。我们表明,用G-卷积替换平面卷积一致地改善了结果,而无需额外的调谐。在第9节中,我们提供了这些结果的讨论,并考虑几个扩展的方法,在第10节结束之前。
2.结构化和等变表示
深度神经网络通过一系列参数化函数映射输入来产生一系列逐渐更抽象的表示(LeCun et al.2015)。在当前一代的神经网络中,表示空间通常具有非常小的内部结构,例如线性空间Rn。
在本文中,我们构造的表示,具有一个线性G-空间的结构,对于一些选定的群G。这意味着表示空间中的每个向量都具有与其相关联的姿态,该姿态可以通过某个变换组G的元素进行变换。这种额外的结构使我们能够更有效地建模数据:G-CNN中的滤波器检测具有优选相对姿态的特征的共现,并且可以通过称为G卷积的操作在每个全局姿态中匹配这样的特征星座。
一个表示空间可以从它所连接的其他表示空间获得它的结构。为了实现这一点,将一个表示映射到另一个表示的网络或层Φ应该是结构保留的。对于G-空间,这意味着Φ必须是等变的:
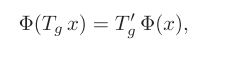
也就是说,通过变换g(Tg x)来变换输入x,然后将其传递通过学习的映射Φ,应该给予与首先将x映射到Φ然后变换表示相同的结果。
等变性可以通过许多方式实现,特别是算子T和T′不需要相同。对T和T′的唯一要求是,对于任意两个变换g和h,我们有T(gh)= T(g)T(h)(即T是G的线性表示)。
从等式1中我们看到,我们熟悉的不变性概念是一种特殊的等变性,其中T′ g是所有g的恒等变换。在深度学习中,广义等方差比不变性更有用,因为如果特征是不变的,就不可能确定它们是否处于正确的空间配置。