动态规划（Dynamic Programing）

动态规划就是通过记住过去所算过的值，来防止重复计算所带来的弊端。这就是为什么动态规划也可以写成记忆化搜索的形式。

下面，我们通过 DP 的题目，假设我们对其的感悟！（大家可以边看边做一下这几道题，都是很好的题目）

---

第一关：线性DP

第一战：$CF191A.DynastyPuzzles$

题目描述

难度：$☆☆☆$

题目大意

题目描述

有一个王朝，他们国王的名字用姓氏的简写来标记每一代。为了保证王朝的稳定，现在这个王朝的继承人的名字需要满足继承者名字的第一个字母要和前代名字最后一个字母相同。然后拼接起来的名字，第一个字母和最后一个字母相同。现在有一个考古博士，知道了这个王朝国王和亲戚的名字。问你这个王朝所能够得到的最长字符串。

输入

第一行一个整数 $n$ ($1\le n\le 5\cdot 10^5$)，接下来 $n$行，每行一个非空字符串，全由小写字母组成，字符串长度不超过 $10$。

输出

最长满足要求的长度，如果没有输出 $0$。

---

思路

动态规划莫过于 $4$ 步：

1. 状态的定义
2. 转移的推导
3. 边界的确定
4. 结果的输出

状态的定义：

可以设 $f_{i,j}$ 表示当前名字的第一个字母为 $i$，最后一个字母为 $j$ 的最长串。
但是，字母不容易开数组，所以我们可以将其压缩成 $0\sim 26$ 的整数。

---

转移的推导

之后，我们不难想到对于每一个长度为 $n$ 字符串 $S$，$f_{j,S_n}=max(f_{j,S_n},f_{j,S_1}+n)$。
注意，如果这是我们所拼接的第一个串，那么 $f_{S_1,S_n}=n$，不能在通过上面的转移方式转移，因为第一个字母只能是 $S_1$

---

边界的确定

因为，我们要确定每一个串是否是我们拼接的第一个串，所以我们上来要把 $f$ 数组全部赋值为 $int$ 的最小值。

---

结果的输出

那么这道题最终他的名字其实就是首位字母相同的串，故所有串中首位相同的最长串即为答案！
$$res=max(f_{i,i})$$

一首小诗作为总结：

名字首 $i$ 最后 $j$，状态设为 $f_{i,j}$
方程转移枚举头，加入 $i$ 串转移透。
边界一定要注意，设小为保第一串。
最后结果首尾同，即为最值 $f_{i,i}$

---

时间复杂度：$O(n)$

代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int N = 30;

int n;
string name;
int f[N][N];

signed main()
{
	cin >> n;
	
	memset(f, -0x3f, sizeof f);
	for (int i = 1; i <= n; i ++)
	{
		cin >> name;
		int len = name.size(), l = name[0] - 'a', r = name.back() - 'a';
		for (int j = 0; j < 26; j ++)
			f[j][r] = max(f[j][r], f[j][l] + len);
		f[l][r] = max(f[l][r], len); //初始所有值都是-0x3f3f3f3f，所以取个max就能够让第一个串赋值
	}
	
	int res = 0;
	for (int k = 0; k < 26; k ++)
		res = max(res, f[k][k]);
		
	cout << res << endl;
	
	return 0;
}

恭喜您，成功战胜了$CF191A.DynastyPuzzles$，奖励怪兽等级一份：

$BronzeMonster$
$UnusualMonster$
$EpicMonster$
$LegendaryMonster$

---

第二战：$CF455A.Boredom$

题目描述

难度：$☆☆$

题目大意

给定一个有 $n$ 个元素的序列 { a n } \{a_n\} {an​}。你可以做若干次操作。在一次操作中我们可以取出一个数（假设他为 $x$）并删除它，同时删除所有的序列中值为 $x+1$ 和 $x-1$ 的数。这一步操作会给玩家加上 $x$ 分。

输入

输入格式 第一行一个整数 $n(1\le n\le 10^5)$,说明这个序列有多少数。 第二行 $n$ 个整数，分别表示 $a_1,a_2,\cdots ,a_n$。

输出

一个整数，表示玩家最多能获得多少分

---

思路

动态规划 $4$ 步：

1. 状态的定义
2. 转移的推导
3. 边界的确定
4. 结果的输出

状态的定义：

首先我们会想到设 $f_{i,0/1}$ 表示 $a_i$删除或者是不删除，但是发现不是很好转移，于是我们可以

嘿嘿，才怪。故而，我们再想一想，他前后删除的是所有值，所以设 $f_{i,0/1}$ 表示前 $i$ 个数中，数字 $i$ 删除还是不删除会不会简单一些呢？

---

转移的推导

不难想到，设 $cn{t}_i$ 为 $i$ 出现的次数，
$$\{\begin{array}{ll}& f_{i,1}=max(f_{i-2,0},f_{i-2,1})+cn{t}_i\times i\\ & f_{i,0}=max(f_{i-1,1},f_{i-1,0})\end{array}$$
因为，如果选了数 $i$，那么贡献就是 $cn{t}_i\times i$，那么 $i-1$ 也一定不能选。但是 $i-2$ 是可以选的呀！如果不选数 $i$，那么就考虑 $i-1$选不选。

---

边界的确定

---

结果的输出

不难想，就是 $max(f_{mx,0},f_{mx,1})$，$mx$表示序列中最大的元素。
因为，我们考虑了前面所有的元素，最终就是这两个取其一！

一首小诗总结一下

这题状态要小心，不设下标却设数。
转移若选找前 $2$，如果不选看前值。
边界确定仔细想，貌似根本不需要。
最终结果找 $mx$，选或不选取个 $max$。

---

时间复杂度：$O(n)$

代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int N = 1e5 + 10;

int n;
int a[N], f[N][2], cnt[N];

signed main()
{
	cin >> n;
	
	int mx = 0;
	for (int i = 1; i <= n; i ++)
		cin >> a[i], cnt[a[i]] ++, mx = max(mx, a[i]);
		
	for (int i = 1; i <= mx; i ++)
	{
		f[i][1] = max(f[i - 2][1], f[i - 2][0]) + cnt[i] * i;
		f[i][0] = max(f[i - 1][1], f[i - 1][0]);
	}
		
	cout << max(f[mx][1], f[mx][0]) << endl;
	
	return 0;
}

恭喜您，成功战胜了$CF455A.Boredom$，奖励继续看题（嘿嘿）

---

第三战：$CF1061C.Multiplicity$

题目描述

难度：$☆☆☆$

题目大意

从序列 { a 1 ,   a 2 ,   . .   ,   a n } \{a_1,\ a_2,\ ..\ ,\ a_n\} {a1​, a2​, .. , an​} 中选出非空子序列 { b 1 ,   b 2 ,   . .   ,   b k } \{b_1,\ b_2,\ ..\ ,\ b_k\} {b1​, b2​, .. , bk​}，一个子序列合法需要满足 $\forall i\in [1,k],i|b_i$。求有多少互不相等的合法子序列，答案对 $10^9+7$ 取模。

序列 { 1 ,   1 } \{1,\ 1\} {1, 1} 有 $2$ 种选法得到子序列 { 1 } \{1\} {1}，但 $1$ 的来源不同，认为这两个子序列不相等。

思路

动态规划需要 $5$ 步了：

1. 状态的定义
2. 转移的推导
3. 边界的确定
4. 结果的输出
5. 动归的优化

状态的定义：

由于题意中设计到了第 $i$ 个数必须被 $i$整除，所以我们可以想到长度，于是可以考虑用 $f_{i,j}$ 表示对于前 $i$ 个数来说，长度为 $j$ 的方案数。

---

转移的推导

$$\{\begin{array}{llc}& f_{i,j}=f_{i,j}+f_{i-1,j}& j\mid a_i\\ & f_{i,j}=f_{i-1,j}& otherwise\end{array}$$
因为，如果 $a_i$ 是 $j$ 的倍数，那么就可以加入序列中，所以可以加上前一个长度。反之，不可以，不能加入，所以长度不减 $1$。

---

边界的确定

起初，长度为 $0$ 时规定有一种转移方式，即 $f_{0,0}=1$。

---

结果的输出

最终的结果就是所有可能长度之和，即 $res=\sum _{i=1}^n{f}_{n,i}$

---

动归的优化

这道题涉及到了动态规划的优化，因为我们会发现，两维的状态根本开不出来，会炸！
所以，这时候，细心地我们发现转移的时候只用到了 $i-1$，那么我们就可以仿照01背包的方式，用个滚动数组把第一维滚掉，当然这样在枚举长度的时候要倒着枚举！
OK，数组是开下了，可是时间呢？还是炸，我们不妨算一下，#^&%!$# ……*&%￥&@，时间复杂度 $O(n^2)$！完了，芭比球了！

没事，不要慌，慌你就输了。我们再细心的观察一下，就会发现，咦好像只有在 $j\mid a_i$的时候才可以转移，所以我们就能够先把 $a_i$ 的约数列出来（$O(\sqrt{n})$），然后进行转移（$O\sqrt{(}n)$）。

诶？好像可以了诶，时间复杂度到了 $O(n\sqrt{n})$，这样就可以跑过去了！

---

一首小诗总结一下

状态无妨设两维，之后再用滚动压。
转移只当 $j\mid a$，所以可以找约数。
边界 $0$ 长设为 $1$，之后才可好转移。
最后求和所有长，直接输出 $AC$ 现。

---

时间复杂度：$O(n\sqrt{n})$

代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int N = 1e6 + 10, mod = 1e9 + 7;

int n;
int a[N];
int f[N];
vector<int> gt;

signed main()
{
	cin >> n;
	
	f[0] = 1;
	for (int i = 1; i <= n; i ++)
	{
		cin >> a[i];
		gt.clear();
		for (int j = 1; j <= a[i] / j; j ++)
			if (a[i] % j == 0)
			{
				gt.push_back(j);
				if (a[i] / j != j) gt.push_back(a[i] / j);
			}
		
		sort(gt.begin(), gt.end(), greater<int>());
		for (auto c : gt)
			f[c] = (f[c] + f[c - 1]) % mod;
	}
	
	int res = 0;
	for (int i = 1; i <= n; i ++)
		res = (res + f[i]) % mod;
		
	cout << res << endl;
	
	return 0;
}

恭喜您，成功战胜了$CF1061C.Multiplicity$，奖励一次问而必答的机会，验证码6AZ70（好像没什么用 ）＋简单题讲解。

---

第四战：$ABC311E-DefectfreeSquares$

题目描述

题目大意

给出一个 $H\times W$ 的矩阵，每个位置要么有洞，要么没洞，问有多少个每个元素均为正整数的三元组 $(x,y,n)$，满足：

$x+n-1\le H$，$y+n-1\le W$，以 $(x,y)$ 为左上角、$(x+n-1,y+n-1)$ 为右下角的矩阵每个位置都没有洞。

$H,W\le 3000$，洞的个数不超过 $10^5$。

---

思路

动态规划 $4$ 步：

1. 状态的定义
2. 转移的推导
3. 边界的确定
4. 结果的输出

状态的定义

我们不难想到设 $f_{i,j}$ 表示以 $(i,j)$ 正方形右下角的方案数。（这并不是本题的难点）

转移的推导（难点）

对于每一个 $f_{i,j}$，我们考虑他的推导：

• 如果 $A_{i,j}$ 为洞，那么不会有合法的正方形，故 $f_{i,j}=0$
• 如果 $A_{i,j}$ 不为洞，那么考虑从三个方向转移：
  • 那么$f_{i,j}=\min (f_{i-1,j},f_{i,j-1},f_{i-1,j-1})+1$，首先，这里的 $+1$ 就是会多出 $i,j$ 自己作为一个正方形，对于取 $\min$ 的段落，就是通过 $3$ 个点来确定出从 $(i,j)$ 这个点可以向外延伸多长，下面有几个误区澄清一下：
  • 误区1：有些人会考虑取最大值
    • 这是不对的，考虑设 $x_1$ 为以 $i-1,j$ 为右下角的合法正方形的最大边长，$x_2$ 为以 $i-1,j-1$ 为右下角的合法正方形的最大边长，$x_3$ 为以 $i-1,j-1$ 为右下角的合法正方形的最大边长。其实 $x_1,x_2,x_3$ 就是我们的 $f_{i-1,j},f_{i,j-1},f_{i-1,j-1}$，因为如果边长为$x_1$的正方形是合法的，那么比 $x_1$ 边长小的正方形也一定合法，又因为我们取得是最大边长，所以就等同于 $f_{i-1,j},f_{i,j-1},f_{i-1,j-1}$。之后，我们考虑假设 $x_1$ 最大，那难道答案就是 $x_1$吗？当然不是，因为 $(i-x_3,j-x_3)$这个点一定是有洞的，那么如果按我们的理解从 $(i-x_1,j-x_1+1)$ 到 $(i,j)$都是无洞的。但是 $i-x_1<i-x_3$ 且 $j-x_1+1\le j-x_3$，所以一定包含点 $(i-x_3,j-x_3)$，即答案不是 $x_1$。以此类推，我们就可以证明出答案其实是最小值
  • 误区2：有些人会认为可以不加 $(i-1,j-1)$
    • 这个很好反驳，给个例子就行了
      
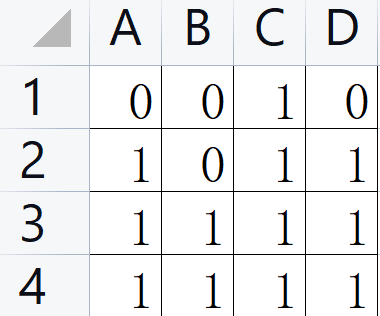
      假设，我们当前枚举到了 $D4$，那么如果光通过 $D3$ 和 $C4$ 转移，方案数为 $2$，不过真的对吗？其实是错的因为 $B2$ 这个点并没有在状态之内，就会发生状态的遗漏。所以，必须加入 $(i-1,j-1)$，这样才能保证，正方形区域内全是 $1$。

边界的确定

结果的输出

最终答案不难想，就是以每个 $(i,j)$ 为正方形右下角的方案数之和，即 $res=\sum _{i=1}^n\sum _{j=1}^m{f}_{i,j}$

一首小诗总结一下

---

代码

#include <iostream>
#define int long long

using namespace std;

const int N = 3e3 + 10;

int n, m, k;
int a, b;
int mp[N][N], dp[N][N];

signed main()
{
	cin >> n >> m >> k;
	
	for (int i = 1; i <= k; i ++)
			cin >> a >> b, mp[a][b] = 1;
			
	int res =0 ;
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++)
		{
			dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
			if (mp[i][j])
				dp[i][j] = 0;
			res += dp[i][j];
		}
		
	cout << res << endl;
	
	return 0;
}

时间复杂度：$O(nm)$

恭喜你，成功战胜了$ABC311E-DefectfreeSquares$，奖励继续看题~~~

---

第五战：$CSES-1638GridPaths$

题目描述

题目大意

给出一个 $n\times n$ 的网格，其中 * 表示当前点不可走，.表示当前点可走，每次只能向右或向左走，问从 $(1,1)$ 走到 $(n,n)$ 的方案数，对 $10^9+7$ 取模。

---

思路

动态规划莫过于 $4$ 步：

1. 状态的定义
2. 转移的推导
3. 边界的确定
4. 结果的输出

状态的定义：

可以设 $f_{i,j}$ 表示从 $(1,1)$ 走到 $(i,j)$ 的方案数。

---

转移的推导

比较简单，直接写吧：

$$f_{i,j}=\{\begin{array}{llc}& f_{i,j}+f_{i-1,j}& G_{i-1,j}\ne \ast \\ & f_{i,j}+f_{i,j-1}& G_{i,j-1}\ne \ast \end{array}$$

---

边界的确定

$f_{1,1}=1$

---

结果的输出

$res=f_{n,n}$

一首小诗总结一下

起点至坐标 $(i,j)$，方案设为 $f_{i,j}$
转移先判能否转，之后再加方案数。
边界此时要确定，起点自身 $1$ 方案。
输出终点方案数，天空巨响 $AC$ 现

---

代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int N = 1e3 + 10, mod = 1e9 + 7;

int n;
char g[N][N];
int f[N][N];

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> n;

	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= n; j ++)
			cin >> g[i][j];

	if (g[1][1] != '*') f[1][1] = 1; //注意：如果第一个点是*就不能在往后推导了
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= n; j ++)
		{
			if (g[i][j] == '*') continue;
			int Way1 = f[i - 1][j], Way2 = f[i][j - 1];
			if (g[i - 1][j] == '*') Way1 = 0;
			if (g[i][j - 1] == '*') Way2 = 0;
			f[i][j] = (f[i][j] + Way1 + Way2) % mod;
		}

	cout << f[n][n] << endl;

	return 0;
}

时间复杂度：$O(n^2)$

恭喜您，成功战胜了$CSES-1638GridPaths$，奖励无：

---