来源:力扣(LeetCode)
描述:
有一只跳蚤的家在数轴上的位置 x 处。请你帮助它从位置 0 出发,到达它的家。
跳蚤跳跃的规则如下:
- 它可以 往前 跳恰好
a个位置(即往右跳)。 - 它可以 往后 跳恰好
b个位置(即往左跳)。 - 它不能 连续 往后跳
2次。 - 它不能跳到任何
forbidden数组中的位置。
跳蚤可以往前跳 超过 它的家的位置,但是它 不能跳到负整数 的位置。
给你一个整数数组 forbidden ,其中 forbidden[i] 是跳蚤不能跳到的位置,同时给你整数 a, b 和 x ,请你返回跳蚤到家的最少跳跃次数。如果没有恰好到达 x 的可行方案,请你返回 -1 。
示例 1:
输入:forbidden = [14,4,18,1,15], a = 3, b = 15, x = 9
输出:3
解释:往前跳 3 次(0 -> 3 -> 6 -> 9),跳蚤就到家了。
示例 2:
输入:forbidden = [8,3,16,6,12,20], a = 15, b = 13, x = 11
输出:-1
示例 3:
输入:forbidden = [1,6,2,14,5,17,4], a = 16, b = 9, x = 7
输出:2
解释:往前跳一次(0 -> 16),然后往回跳一次(16 -> 7),跳蚤就到家了。
提示:
- 1 <= forbidden.length <= 1000
- 1 <= a, b, forbidden[i] <= 2000
- 0 <= x <= 2000
- forbidden 中所有位置互不相同。
- 位置 x 不在 forbidden 中。
方法:广度优先搜索
思路
求最短路径一般需要用广度优先搜索,但是此题中的图是个无限图,如果不限制搜索的范围,无法处理无解的情况。因此,解决此题的关键是找出搜索的范围,其中下限已经由题目给出,不能跳到负整数的位置,我们还需要找出搜索的上限,下面分情况讨论:
- a = b。此时为了次数最少,跳蚤没有必要向后跳,只需要一直往前跳。当它超过 x 却没有遇到 x,表示它再也跳不到 x 了,此时的上限可以设置为 x。
- a > b。题目规定,跳蚤不能连续往后跳 2 次,因此这只跳蚤运动轨迹中,任意连续的两次跳跃,总的行程一定是在前进的,前进了 a−ba-ba−b 的距离。即使它某一步是在后退,这一步的前一步和后一步(如果有的话)一定是在前进。此时跳蚤运动的上限为 x + b,在这个上限的情况下,跳蚤往回跳一步可以到达 x。在大于这个上限的情况下,即使跳蚤马上往回跳一步,所处的位置也大于 x,而且跳蚤接下来前进的次数必然会大于等于后退的次数,再也无法到达 x。因此在这种情况下,上限为 x + b。
- a < b。在这种情况下,上限为 max(max(forbidden) + a + b, x)。接下来证明这一点。为了方便,记 max(forbidden) = f。首先,需要将数轴上大于等于 0 的位置分为三个区域:
- [0, f],禁止区。所有 forbidden 中的位置都位于这个区域。
- (f, max(f + a + b, x)],安全区,它的右边界是 a < b 情况下我们想要证明的广度优先搜索的上限。
- (max(f + a + b, x), +∞) ,界外区。
这三个区域合起来组成了数轴上大于等于 0 的所有部分,注意 x 可能位于禁止区或者安全区,但不会是 forbidden 数组中的元素。假设某个步数最少的路径中,点 C 是第一个进入界外区(前进进入)的点,而点 H 是第一个离开界外区(后退离开)的点。因为 x 只可能位于禁止区或者安全区,因此如果这条路径存在点 C,那么必然存在点 H。如下图,横坐标为步数,纵坐标为与原点的距离。箭头朝右上表示前进,箭头朝右下表示后退。

接下来,我们通过交换线段 BC 和线段 GH ,并保持其他线段的的方向不变,来使得点 C 不再位于界外区。如下图,线段 BC’ 变为后退而线段 G’H 变为前进。
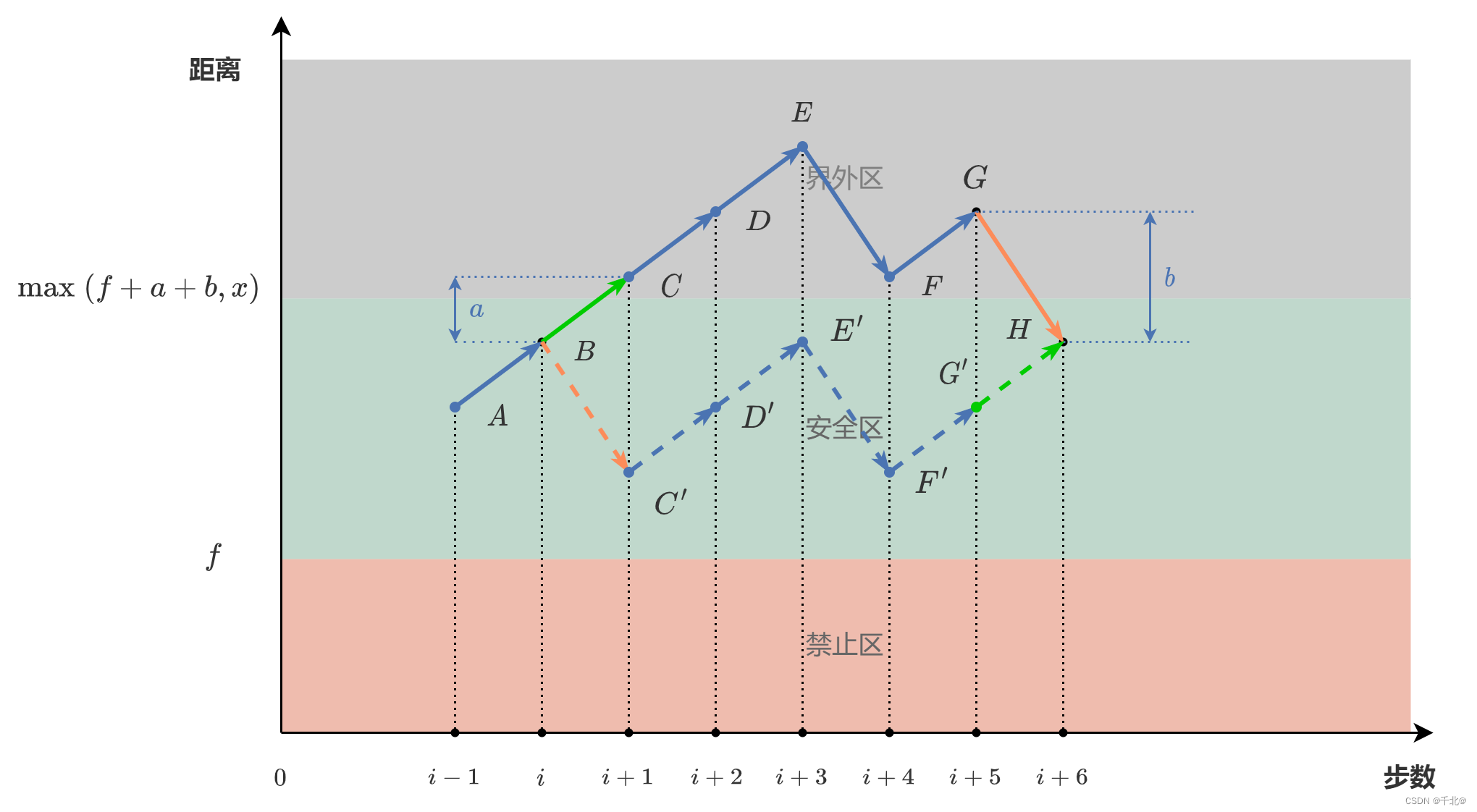
我们从以下几个方面论证这种交换的可行性:
- 交换前,点 C,D,…,F,G 全都位于界外区,与原点的距离大于 f + a + b 。通过交换,这些点与原点的距离缩小了 a + b ,仍然大于 f。因此,这些点不会落到 forbidden 中。
- 交换后不会增加这个路径的步数,也不会影响点 H 之后的点的位置。
- 交换不会造成两次倒退。交换后,前进的线段 BC 变为后退的线段 BC’ ,但是 BC’ 的前一段 AB 一定是前进的。可以利用反证法证明,如果 AB 是后退的,那么点 A 就会在界外区,因为 a < b ,这样的话点 C 就不会是第一个界外区的点,因此 AB 一定是前进的。BC’ 的后一段 C’D’ 一定也是前进的。这里需要分为两种情况:
- CD 原本就是前进的,那么 C’D’ 会保持原来前进的方向。通过交换,我们不会造成两次倒退。
- CD 原本是后退的,那么点 D 就是我们前面讨论的第一个离开界外区的点 H,因为 a < b。这样一来,我们其实是交换了前进的 BC 和后退的 CD,得到了后退的 BC’ 和前进的 C’D,仍然不会造成两次倒退。
通过这样的交换,我们使得一个有效路径第一个进入界外区的点,不再位于界外区。新的路径,第一个进入界外区的点,可能位于点 C 和点 H 之间,也可能位于点 HHH 之后,也可能不存在这样的点。总之,我们可以不停地寻找第一个进入界外区的点,然后经过上述的交换,使得最终的路径的所有点都位于禁止区和安全区。这样,我们就证明出,如果某个输入有解,那么至少有一条最短路径,它的所有点都处于上限 max(f + a + b, x) 之内。因此在这种情况下,上限为 max(max(forbidden) + a + b, x)。
综合以上三种情况,广度优先搜索的上限是 max(max(forbidden) + a, x) + b 。
在进行广度优先搜索时,除了需要注意到上下限,不能达到 forbidden 数组中的坐标,还需要注意到达每个坐标时,都会有前进到达还是后退到达两种状态。如果是前进到达时,下一步可以选择前进或者后退;如果是后退到达时,下一步只能选择前进。因此广度优先搜索的每个元素,需要保存三个信息,坐标,方向和步数。在代码中,我们用 1 表示前进, −1 表示后退,用哈希集合 visited 来记录已经达到过的位置和方向状态。在搜索的过程中,如果坐标第一次为 x,则返回当前步数。当队列为空时,表示 x 不可到达,返回 −1。
代码:
class Solution {
public:
int minimumJumps(vector<int>& forbidden, int a, int b, int x) {
queue<tuple<int, int, int>> q;
unordered_set<int> visited;
q.emplace(0, 1, 0);
visited.emplace(0);
int lower = 0, upper = max(*max_element(forbidden.begin(), forbidden.end()) + a, x) + b;
unordered_set<int> forbiddenSet(forbidden.begin(), forbidden.end());
while (!q.empty()) {
auto [position, direction, step] = q.front();
q.pop();
if (position == x) {
return step;
}
int nextPosition = position + a;
int nextDirection = 1;
if (lower <= nextPosition && nextPosition <= upper && !visited.count(nextPosition * nextDirection) && !forbiddenSet.count(nextPosition)) {
visited.emplace(nextPosition * nextDirection);
q.emplace(nextPosition, nextDirection, step + 1);
}
if (direction == 1) {
nextPosition = position - b;
nextDirection = -1;
if (lower <= nextPosition && nextPosition <= upper && !visited.count(nextPosition * nextDirection) && !forbiddenSet.count(nextPosition)) {
visited.emplace(nextPosition * nextDirection);
q.emplace(nextPosition, nextDirection, step + 1);
}
}
}
return -1;
}
};
时间 32ms 击败 44.76%使用 C++ 的用户
内存 18.11MB 击败 43.81%使用 C++ 的用户
复杂度分析
- 时间复杂度:O(max(max(forbidden)+a,x)+b)。表达式为广度优先搜索的位置上限,每个位置最多会被计算两次。
- 空间复杂度:O(max(max(forbidden)+a,x)+b)。表达式为广度优先搜索的位置上限,是队列和哈希集合的空间复杂度。
author:力扣官方题解