《算法竞赛·快冲300题》每日一题：“浇水”

news2024/7/4 6:34:19

《算法竞赛·快冲300题》将于2024年出版，是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码，以中低档题为主，适合入门、进阶。

文章目录

题目描述
题解
C++代码
Java代码
Python代码

“ 浇水” ，链接： http://oj.ecustacm.cn/problem.php?id=1902

题目描述

【题目描述】 给出 N 滴水的坐标，y 表示水滴的高度，x 表示它下落到 x 轴的位置。
每滴水以每秒 1 个单位长度的速度下落。
你需要把花盆放在 x 轴上的某个位置，使得从被花盆接着的第 1 滴水开始，到被花盆接着的最后 1 滴水结束，之间的时间差至少为 D。
我们认为，只要水滴落到 x 轴上，与花盆的边沿对齐或者在花盆中，就认为被接住。
给出 N 滴水的坐标和 D 的大小，请算出最小的花盆的宽度 W。
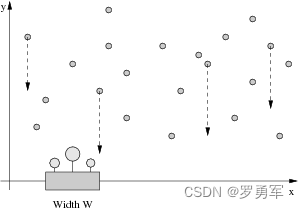
在这里插入图片描述

【输入格式】 第1行：两个整数 N 和 D，1 <= N <= 100,000，1 <= D <= 1,000,000。
接下来 N 行：每行两个整数 x，y，表示雨滴的坐标，0 <= x, y <= 1,000,000。
【输出格式】 仅一行 1 个整数，表示最小的花盆的宽度。
如果无法构造出足够宽的花盆，使得在 D 单位的时间接住满足要求的水滴，则输出 −1。
【输入样例】

【输出样例】

题解

题目的意思有点费解，用样例解释。有n = 4个水滴，把花盆放在某个地方接水滴，从接到第1个水滴开始，到接到最后一个水滴，要求落到花盆的所有水滴的总时间超过d = 6秒。问花盆的最小宽度是多少。答案是选第一个水滴(6, 3)和第三个水滴(4, 10)，它们落到花盆里的时间差是10 - 3 = 7，超过6秒，花盆的宽度是6 - 4 = 2。
下面概况题意。任选一个区间（花盆宽度）[L,R]，统计这个区间内最大值和最小值（最高和最低水滴）的差，如果≥d，称为一个合法区间，记录区间宽度。遍历所有这种合法区间，找到最小宽度，就是答案。
区间问题可以用尺取法，用快慢指针形成的“滑动窗口”遍历所有区间，计算复杂度 $O(n^2)$ ，超时。本题至少需要 $O (n l o g n)$ 复杂度的算法。
用滑动窗口遍历区间的方法，除了尺取法，还有单调队列。《算法竞赛》第10页有一道类似的例题“洛谷P1886”。给定一个固定的窗口宽度k，要求输出所有窗口宽度等于k的区间内的最大最小值。用单调队列求解，复杂度仅为 $O (n)$ 。请仔细阅读这一节的内容，理解为什么复杂度是 $O (n)$ 的。
本题和洛谷P1886相同的地方都是求窗口内最大最小值，区别是本题没有给定固定的窗口宽度。那么用二分法来猜一个最小的k即可：每次猜一个窗口宽度k，用函数check(k)判断窗口宽度为k时有没有合法的区间，函数check()用单调队列求解。“二分法+单调队列”的计算复杂度，二分法猜 $O (l o g n)$ 次，每次用check()求所有宽度为k的区间的最大最小值是 $O (n)$ 的，总复杂度 $O (n l o g n)$ 。
代码中的单调队列是手写的（手写队列见《算法竞赛》，清华大学出版社，罗勇军、郭卫斌著，7页）。h是队头，t是队尾；保持h≤t，队列长度等于t - h + 1；h++表示弹出（删除）队头，t–表示弹走（删除）队尾。
函数check(k)的功能是检查有没有一个宽度为k的合法窗口，这个窗口内的最大最小值差≥d。用两个单调队列分别求窗口内的最大和最小值。q1是单调递增队列，队头是最小值；q2是单调递减队列，队头是最大值。
【重点】 单调队列。

C++代码

#include<bits/stdc++.h>
using namespace std;
const int N=100001;
int n,d;
int q1[N],q2[N];                  //q1队头是窗口内最小值，q2队头是窗口内最大值
struct node{int x,y;}a[N];
int cmp(node u,node v){ return u.x<v.x;}
bool check(int k){
    memset(q1,0,sizeof(q1));      //单调递增，队头最小
    memset(q2,0,sizeof(q2));      //单调递减，队头最大
    int h1=1,t1=0,h2=1,t2=0;      //h:队头，t队尾 ，注意保持 h<=t
    for(int i=1;i<=n;i++){        //a[i]一个个地进入队尾
        while(h1<=t1 && a[q1[h1]].x < a[i].x-k)  h1++;  //窗口宽度大于k了，弹走队头，减小到k
        while(h1<=t1 && a[i].y < a[q1[t1]].y)
            t1--;           //如果原队尾更大，删除队尾，保持队头a[q1[h1]].y最大
        q1[++t1]=i;         //现在队内都比a[i]小了，a[i]从队尾进队
        //前面几行求窗口内的最小值，下面几行求窗口内的最大值
        while(h2<=t2 && a[q2[h2]].x < a[i].x-k)  h2++;  //窗口宽度大于k了，弹走队头，减小到k
        while(h2<=t2 && a[i].y > a[q2[t2]].y)
            t2--;           //如果原队尾更小，删除队尾，保持队头a[q2[h2]].y最大
        q2[++t2]=i;         //现在队内都比a[i]大了，a[i]从队尾进队

        if(a[q2[h2]].y-a[q1[h1]].y >= d) return true; //最大最小之差大于等于d
    }
    return false;
}
int main(){
    cin>>n>>d;
    for(int i=1;i<=n;i++)  scanf("%d%d",&a[i].x,&a[i].y);
    sort(a+1,a+n+1,cmp);     // 根据x值升序
    int L=1,R=1e6,ans=-1;
    while(L<=R){             //二分求最小宽度
        int mid=(L+R)>>1;
        if(check(mid)) ans=mid,R=mid-1;
        else  L=mid+1;
    }
    cout<<ans<<endl;
    return 0;
}

Java代码

import java.util.*;
import java.io.*;
class Main {
    static class Node {
        int x, y; 
        Node(int x, int y) {
            this.x = x;
            this.y = y;
        }
    } 
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int d = scanner.nextInt();
        Node[] a = new Node[n + 1];
        for (int i = 1; i <= n; i++) {
            int x = scanner.nextInt();
            int y = scanner.nextInt();
            a[i] = new Node(x, y);
        }
        Arrays.sort(a, 1, n + 1, (u, v) -> u.x - v.x);
        int L = 1, R = 1000000, ans = -1;
        while (L <= R) {
            int mid = (L + R) >> 1;
            if (check(a, n, d, mid)) {
                ans = mid;
                R = mid - 1;
            } else {
                L = mid + 1;
            }
        }
        System.out.println(ans);
    }
 
    static boolean check(Node[] a, int n, int d, int k) {
        int[] q1 = new int[n+10];
        int[] q2 = new int[n+10];
        int h1 = 1, t1 = 0, h2 = 1, t2 = 0;
        for (int i = 1; i <= n; i++) {
            while (h1 <= t1 && a[q1[h1]].x < a[i].x - k) 
                h1++;
            while (h1 <= t1 && a[i].y < a[q1[t1]].y) 
                t1--;
            q1[++t1] = i; 
            while (h2 <= t2 && a[q2[h2]].x < a[i].x - k) 
                h2++;
            while (h2 <= t2 && a[i].y > a[q2[t2]].y) 
                t2--;
            q2[++t2] = i; 
            if (a[q2[h2]].y - a[q1[h1]].y >= d) 
                return true;
        }
        return false;
    }
}

Python代码

 #pypy
 import sys
input = sys.stdin.readline
def check(a, n, d, k):
    q1 = [0] * (n + 1)
    q2 = [0] * (n + 1)
    h1, t1, h2, t2 = 1, 0, 1, 0
    for i in range(1, n + 1):
        while h1 <= t1 and a[q1[h1]][0] < a[i][0] - k:    h1 += 1
        while h1 <= t1 and a[i][1] < a[q1[t1]][1]:        t1 -= 1
        t1 += 1
        q1[t1] = i
 
        while h2 <= t2 and a[q2[h2]][0] < a[i][0] - k:    h2 += 1
        while h2 <= t2 and a[i][1] > a[q2[t2]][1]:        t2 -= 1
        t2 += 1
        q2[t2] = i
 
        if a[q2[h2]][1] - a[q1[h1]][1] >= d:   return True
    return False
  
n, d = map(int, input().split())
a = [(0,0)]
for _ in range(n):
    x, y = map(int, input().split())
    a.append((x, y))
a.sort()
L, R, ans = 1, 1000000, -1
while L <= R:
    mid = (L + R) >> 1
    if check(a, n, d, mid):
        ans = mid
        R = mid - 1
    else:  L = mid + 1
print(ans)