1.案例背景

1.1遗传算法概述

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。它最初由美国Michigan大学的J. Holland教授提出,1967年, Holland 教授的学生 Bagley在其博士论文中首次提出了“遗传算法”一词,他发展了复制、交叉、变异,显性、倒位等遗传算子。Holland教授用遗传算法的思想对自然和人工自适应系统进行了研究,提出了遗传算法的基本定理——模式定理(schematheorem)。20世纪80年代,Holland教授实现了第一个基于遗传算法的机器学习系统,开创了遗传算法机器学习的新概念。
遗传算法模拟了自然选择和遗传中发生的复制、交叉和变异等现象,从任一初始群体(population)出发,通过随机选择、交叉和变异操作,产生一群更适应环境的个体,使群体进化到搜索空间中越来越好的区域,这样一代一代地不断繁衍进化,最后收敛到一群最适应环境的个体(individual),求得问题的最优解。遗传算法的基本计算流程如图36-1所示。

遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体组成。因此,第一步需要实现从表现型到基因型的映射,即编码工作。初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择个体,并借助于自然遗传学的遗传算子(genetic opera-tors)进行组合交叉和变异,产生出代表新的解集的种群。这个过程将导致种群像自然进化一样,后生代种群比前代更加适应环境,末代种群中的最优个体经过解码(decoding)可以作为问题近似最优解。
遗传算法有三个基本操作:选择(selection)、交叉( crossover)和变异(mutation)。

        (1）选择
        选择的目的是为了从当前群体中选出优良的个体，使它们有机会作为父代为下一代繁衍子孙。根据各个个体的适应度值,按照一定的规则或方法从上一代群体中选择出一些优良的个体遗传到下一代种群中。选择的依据是适应性强的个体为下一代贡献一个或多个后代的概率大。
        (2）交叉
        通过交叉操作可以得到新一代个体,新个体组合了父辈个体的特性。将群体中的各个个体随机搭配成对,对每一个个体,以交叉概率交换它们之间的部分染色体。
        (3）变异
        对种群中的每一个个体,以变异概率改变某一个或多个基因座上的基因值为其他的等位基因。同生物界中一样,变异发生的概率很低,变异为新个体的产生提供了机会。

1.2自变量降维概述

在现实生活中，实际问题很难用线性模型进行描述。神经网络的出现大大降低了模型建立的难度和工作量。只需将神经网络看成是一个黑箱子,根据输入与输出数据,神经网络依据相关的学习规则,便可以建立相应的数学模型。但是,当数学模型的输人自变量(即影响因素)很多,输人自变量之间不是相互独立时,利用神经网络容易出现过拟合现象,从而导致所建立的模型精度低,建模时间长等问题。因此,在建立模型之前,有必要对输入自变量进行优化选择,将冗余的一些自变量去掉,选择最能反映输入与输出关系的自变量参与建模。
近年来,许多人对自变量压缩降维问题进行了深入的研究,取得了一定的成果。常用的变量压缩方法有多元回归与相关分析法、类逐步回归法、主成分分析法、独立成分分析法、主基底分析法、偏最小二乘法、遗传算法等,具体请参考本章文献。

1.3问题描述

威斯康辛大学医学院经过多年的收集和整理,建立了一个乳腺肿瘤病灶组织的细胞核显微图像数据库。数据库中包含了细胞核图像的10个量化特征(细胞核半径、质地、周长、面积、光滑性、紧密度、凹陷度、凹陷点数、对称度、断裂度),这些特征与肿瘤的性质有密切的关系。因此，需要建立-一个确定的模型来描述数据库中各个量化特征与肿瘤性质的关系,从而可以根据细胞核显微图像的量化特征诊断乳腺肿瘤是良性还是恶性的。

建立模型时选用的每个样本(即病例)数据包括10个量化特征(细胞核半径、质地、周长、面积,光滑性、紧密度、凹陷度、凹陷点数、对称度、断裂度)的平均值、10个量化特征的标准差和10个量化特征的最坏值(各特征的3个最大数据的平均值)共30个数据。显然,这30个输人自变量相互之间存在一定的关系,并非相互独立的,因此,为了缩短建模时间、提高建模精度,有必要将30个输入自变量中起主要影响因素的自变量筛选出来参与最终的建模

2模型建立

2.1设计思路

利用遗传算法进行优化计算,需要将解空间映射到编码空间,每个编码对应问题的一个解(即为染色体或个体)。这里,将编码长度设计为30,染色体的每一位对应一个输入自变量,每一位的基因取值只能是“1”和“0”两种情况,如果染色体某一位值为“1”,表示该位对应的输人自变量参与最终的建模;反之,则表示“0”对应的输入自变量不作为最终的建模自变量。选取测试集数据均方误差的倒数作为遗传算法的适应度函数,这样,经过不断地迭代进化,最终筛选出最具代表性的输入自变量参与建模

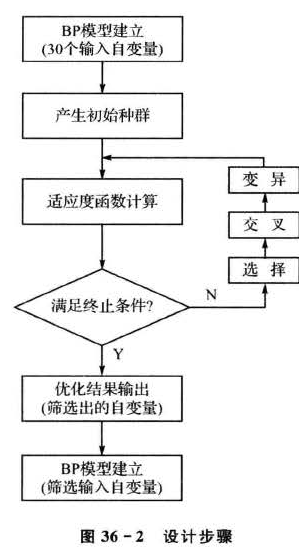
2.2设计步骤

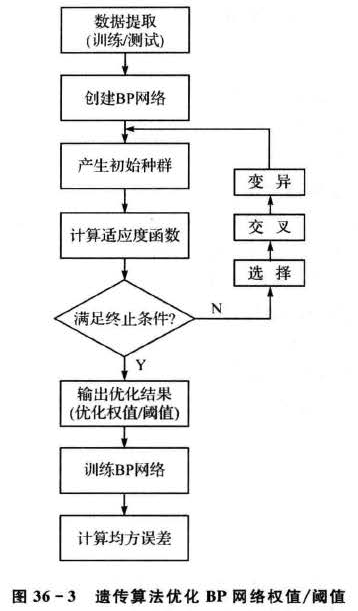
根据上述设计思路,设计步骤主要包括以下几个部分,如图36-2所示。

        1.单BP模型建立
        为了比较遗传算法优化前后的预测效果,先利用全部的30个输入自变量建立BP模型。
        2．初始种群产生
        随机产生N个初始串结构数据,每个串结构数据即为一个个体,N个个体构成了一个种群。遗传算法以这N个串结构作为初始点开始迭代。如前文所述,这里每个个体的串结构数据只有“1”和“0”两种取值。
        3．适应度函数计算
        遗传算法中使用适应度这个概念来度量群体中各个个体在优化计算中可能达到、接近或有助于找到最优解的优良程度。适应度较高的个体遗传到下一代的概率就相对较大。度量个体适应度的函数称为适应度函数。这里,选取测试集数据误差平方和的倒数作为适应度函数:

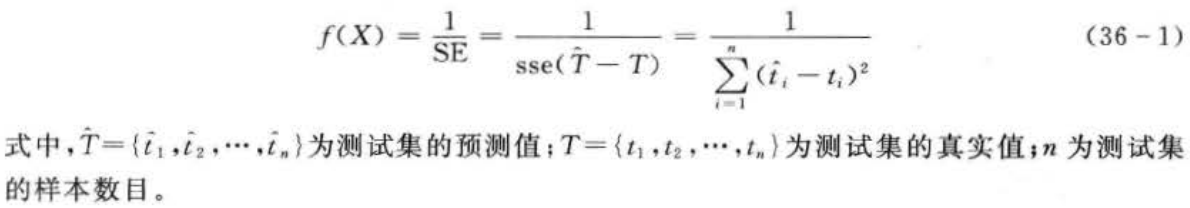
为了避免初始权值和阈值的随机性对适应度函数计算的影响,针对每一个体计算适应度函数值时,均用遗传算法对所建立的BP神经网络的权值和阈值进行优化,优化步骤如图36-3所示。

        4.选择操作
        选择操作选用比例选择算子,即个体被选中并遗传到下一代种群中的概率与该个体的适应度大小成正比,具体的操作过程如下:
        5．交叉操作
        对于输入自变量的压缩降维,交叉操作采用最简单的单点交叉算子,交叉算子原理如图36-4所示。具体操作过程为;

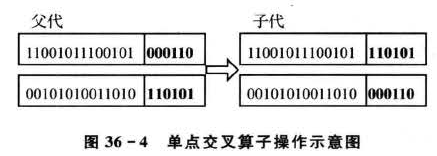
①.先对种群中的个体进行两两随机配对,本案例中产生的初始种群大小为20,故共有10对互相配对的个体组。

②.对每一对相互配对的个体,随机选取某一基因座之后的位置作为交叉点;
③.对每一对相互配对的个体,根据②中所确定的交叉点位置,相互交换两个个体的部分染色体,产生出两个新个体。

6．变异操作
对于输入自变量的压缩降维,变异操作采用最简单的单点变异算子,变异算子原理如图36-5所示。具体操作过程如下:

①随机产生变异点;
②根据①中的变异点位置,改变其对应的基因座上的基因值,由于本案例中的基因值只能取“1”和“0”,所以变异操作的结果即为“1”变为“0”或“0”变为“1”。
对于BP神经网络初始权值和阈值的优化,变异选用非均匀变异算子,具体实现过程见第4节。

        7．优化结果输出
        经过一次次的迭代进化,当满足迭代终止条件时,输出的末代种群对应的便是问题的最优解或近优解,即筛选出的最具代表性的输人自变量组合。
        8．优化BP模型建立
        根据优化计算得到的结果,将选出的参与建模的输人自变量对应的训练集和测试集数据提取出来,利用BP神经网络重新建立模型进行仿真测试,从而进行结果分析。

3 遗传算法工具箱(GAOT)函数介绍

遗传算法工具箱GAOT中含有丰富的遗传算法函数,利用遗传算法工具箱可以很方便地实现遗传算法优化计算。

如果没有安装GAOT工具箱，可以参考这个博客进行下载：

matlab遗传算法gaot工具箱安装

主函数代码如下：

%% 遗传算法的优化计算——输入自变量降维

%% 清空环境变量
clear all
clc
warning off
%% 声明全局变量
global P_train T_train P_test T_test  mint maxt S s1
S = 30;
s1 = 50;
%% 导入数据
load data.mat
a = randperm(569);
Train = data(a(1:500),:);
Test = data(a(501:end),:);
% 训练数据
P_train = Train(:,3:end)';
T_train = Train(:,2)';
% 测试数据
P_test = Test(:,3:end)';
T_test = Test(:,2)';
% 显示实验条件
total_B = length(find(data(:,2) == 1));
total_M = length(find(data(:,2) == 2));
count_B = length(find(T_train == 1));
count_M = length(find(T_train == 2));
number_B = length(find(T_test == 1));
number_M = length(find(T_test == 2));
disp('实验条件为：');
disp(['病例总数：' num2str(569)...
      '  良性：' num2str(total_B)...
      '  恶性：' num2str(total_M)]);
disp(['训练集病例总数：' num2str(500)...
      '  良性：' num2str(count_B)...
      '  恶性：' num2str(count_M)]);
disp(['测试集病例总数：' num2str(69)...
      '  良性：' num2str(number_B)...
      '  恶性：' num2str(number_M)]);
%% 数据归一化
[P_train,minp,maxp,T_train,mint,maxt] = premnmx(P_train,T_train);
P_test = tramnmx(P_test,minp,maxp);
%% 创建单BP网络
t = cputime;
net_bp = newff(minmax(P_train),[s1,1],{'tansig','purelin'},'trainlm');
% 设置训练参数
net_bp.trainParam.epochs = 1000;
net_bp.trainParam.show = 10;
net_bp.trainParam.goal = 0.1;
net_bp.trainParam.lr = 0.1;
net_bp.trainParam.showwindow = 0;
%% 训练单BP网络
net_bp = train(net_bp,P_train,T_train);
%% 仿真测试单BP网络
tn_bp_sim = sim(net_bp,P_test);
% 反归一化
T_bp_sim = postmnmx(tn_bp_sim,mint,maxt);
e = cputime - t;
T_bp_sim(T_bp_sim > 1.5) = 2;
T_bp_sim(T_bp_sim < 1.5) = 1;
result_bp = [T_bp_sim' T_test'];
%% 结果显示（单BP网络）
number_B_sim = length(find(T_bp_sim == 1 & T_test == 1));
number_M_sim = length(find(T_bp_sim == 2 &T_test == 2));
disp('(1)BP网络的测试结果为：');
disp(['良性乳腺肿瘤确诊：' num2str(number_B_sim)...
      '  误诊：' num2str(number_B - number_B_sim)...
      '  确诊率p1 = ' num2str(number_B_sim/number_B*100) '%']);
disp(['恶性乳腺肿瘤确诊：' num2str(number_M_sim)...
      '  误诊：' num2str(number_M - number_M_sim)...
      '  确诊率p2 = ' num2str(number_M_sim/number_M*100) '%']);
disp(['建模时间为：' num2str(e) 's'] );
%% 遗传算法优化
popu = 20;  
bounds = ones(S,1)*[0,1];
% 产生初始种群
initPop = randint(popu,S,[0 1]);
% 计算初始种群适应度
initFit = zeros(popu,1);
for i = 1:size(initPop,1)
    initFit(i) = de_code(initPop(i,:));
end
initPop = [initPop initFit];
gen = 100; 
% 优化计算
[X,EndPop,BPop,Trace] = ga(bounds,'fitness',[],initPop,[1e-6 1 0],'maxGenTerm',...
    gen,'normGeomSelect',0.09,'simpleXover',2,'boundaryMutation',[2 gen 3]);
[m,n] = find(X == 1);
disp(['优化筛选后的输入自变量编号为:' num2str(n)]);
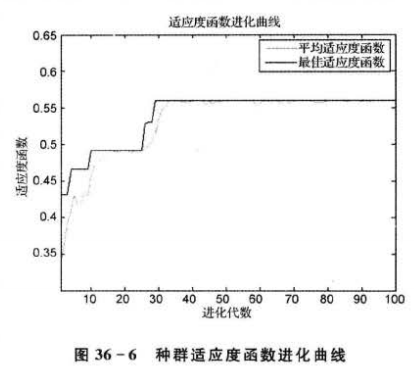
% 绘制适应度函数进化曲线
figure
plot(Trace(:,1),Trace(:,3),'r:')
hold on
plot(Trace(:,1),Trace(:,2),'b')
xlabel('进化代数')
ylabel('适应度函数')
title('适应度函数进化曲线')
legend('平均适应度函数','最佳适应度函数')
xlim([1 gen])
%% 新训练集/测试集数据提取
p_train = zeros(size(n,2),size(T_train,2));
p_test = zeros(size(n,2),size(T_test,2));
for i = 1:length(n)
    p_train(i,:) = P_train(n(i),:);
    p_test(i,:) = P_test(n(i),:);
end
t_train = T_train;
%% 创建优化BP网络
t = cputime;
net_ga = newff(minmax(p_train),[s1,1],{'tansig','purelin'},'trainlm');
% 训练参数设置
net_ga.trainParam.epochs = 1000;
net_ga.trainParam.show = 10;
net_ga.trainParam.goal = 0.1;
net_ga.trainParam.lr = 0.1;
net_ga.trainParam.showwindow = 0;
%% 训练优化BP网络
net_ga = train(net_ga,p_train,t_train);
%% 仿真测试优化BP网络
tn_ga_sim = sim(net_ga,p_test);
% 反归一化
T_ga_sim = postmnmx(tn_ga_sim,mint,maxt);
e = cputime - t;
T_ga_sim(T_ga_sim > 1.5) = 2;
T_ga_sim(T_ga_sim < 1.5) = 1;
result_ga = [T_ga_sim' T_test'];
%% 结果显示（优化BP网络）
number_b_sim = length(find(T_ga_sim == 1 & T_test == 1));
number_m_sim = length(find(T_ga_sim == 2 &T_test == 2));
disp('(2)优化BP网络的测试结果为：');
disp(['良性乳腺肿瘤确诊：' num2str(number_b_sim)...
      '  误诊：' num2str(number_B - number_b_sim)...
      '  确诊率p1=' num2str(number_b_sim/number_B*100) '%']);
disp(['恶性乳腺肿瘤确诊：' num2str(number_m_sim)...
      '  误诊：' num2str(number_M - number_m_sim)...
      '  确诊率p2=' num2str(number_m_sim/number_M*100) '%']);
disp(['建模时间为：' num2str(e) 's'] );

运行结果如下：

从上述结果可以看出,经遗传算法优化计算后,筛选出的一组输人自变量编号为: 2, 5, 6, 7, 8, 9, 10, 11,16,19,22,25,26,28,29,30,也就是说,筛选出的16个输入自变量分别为质地、光滑性、紧密度、凹陷度、凹陷点数、对称度、断裂度的平均值,细胞核半径、紧密度及对称度的标准差,质地、光滑性、紧密度、凹陷点数、对称度及断裂度的最坏值。
显而易见,经遗传算法优化筛选后,参与建模的输入自变量个数约为全部输入自变量个数的一半。对比优化筛选前后的 BP网络的测试结果,可以发现,当使用16个筛选出来的输人自变量进行建模时,预测准确率可以达到100%,相比使用全部自变量建立的模型,性能得到了改善和提升。另一方面,优化后的模型建立时间仅为4s左右,而优化前的模型建立需要29 s左右,这也表明,当使用遗传算法对输人自变量进行降维压缩后,建模时间缩短了很多。