本章将会详细讲解以下知识点:
目录
一:栈
1:栈的定义,栈的特点
2:用什么结构来实现栈与原因的分析?
3: (超详解)栈的常用接口并且附上测试用例
二:队列
1:队列的定义,队列的特点
2:用什么结构来实现队列与原因的分析?
3:(超详解)队列的接口并且附上测试用例
正文开始~:-^-
1:栈的定义及其特点
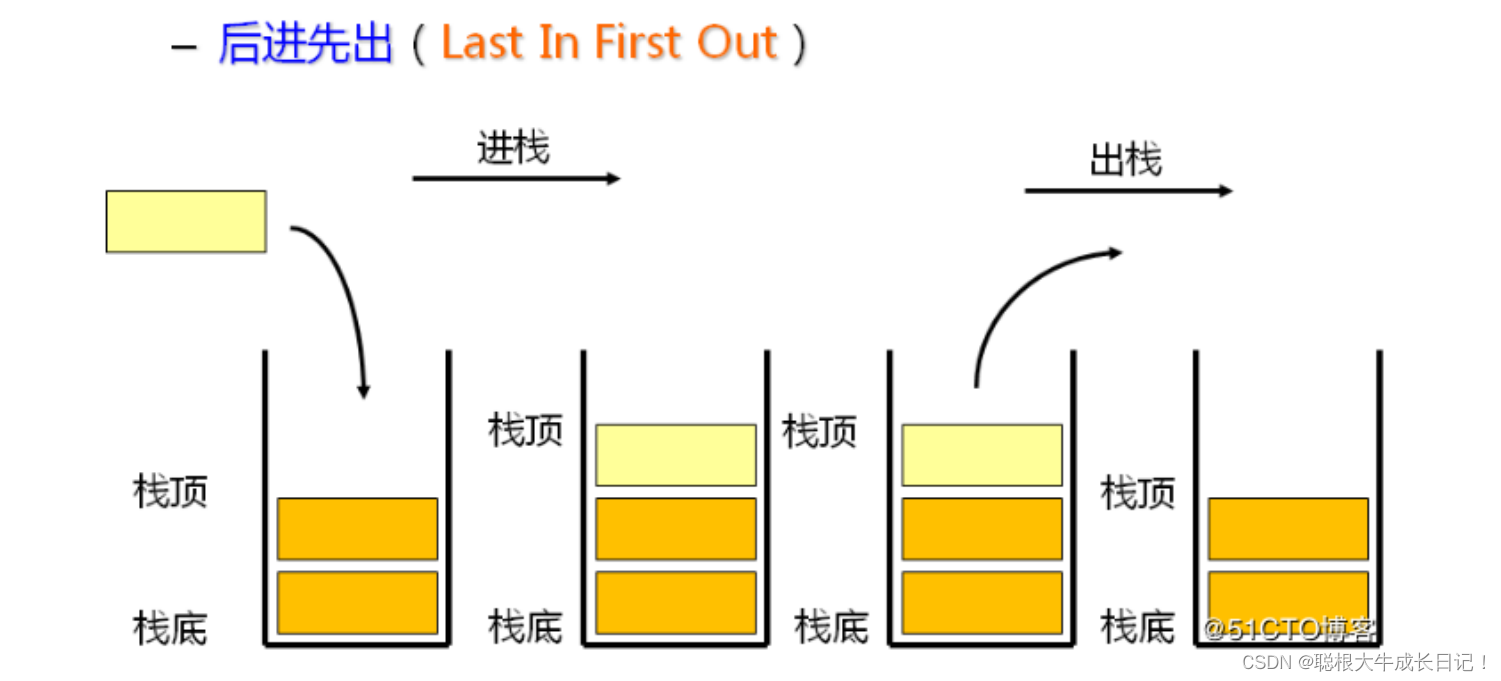
首先栈是一种特殊的线性表,其只能在一端进行插入与删除的操作,进行数据删除与插入的一端我们称它为栈顶,另外一端为栈底。栈中的数据元素遵循后进先出的原则。
下面是栈的操作的叫法:
压栈:表示数据元素插入到栈中,又称为进栈/入栈。入数据在栈顶。
出栈:表示栈中数据元素的删除的操作。出数据在栈顶。
栈的特点:只能在栈的一端进行数据元素的插入与删除,数据元素遵循后进先出的原则。
2:用什么结构来实现栈与原因?
经过前面我们对比顺序表与链表的优缺点,在实现栈的时候我们首选使用顺序表来进行实现栈这种数据结构。当然也可以使用链表来实现。
原因:我们根据栈具有先进后出的特点,它只能在栈顶进行数据元素的插入与删除。
而我们的顺序表就非常适合它,顺序表的尾插与尾删的时间复杂度都是O(1),且顺序表的缓存利用率比链表快,所以顺序表的结构更加优于链表。
3:(详解)栈的常用接口
栈的常用操作有:栈的初始化,栈的销毁,栈的入栈,栈的出栈,获取栈顶元素的值
栈是否为空的判读,栈的大小
在讲解这些接口之前,我们先来讲解栈的定义
包含三个成员变量,S是我们开辟空间的首地址,top是用来记录元素有多少个,同时是数组中元素最后一个元素的下一个位置,capacity是用来表示数组空间容量的大小。
代码如下:
//动态的顺序栈
typedef int STDataType;
typedef struct Stack
{
STDataType* S;
int top;//用来表示栈中最后一个元素的下一个元素的位置
int capacity;
}ST;1:栈的初始化:将三个成员变量的值全部弄为空或者是0
代码如下:
void InitStack(ST* ps)
{
assert(ps);
ps->capacity = 0;
ps->top = 0;
ps->S = NULL;
}
2:栈的入栈操作:每次入栈之前我们先要判断空间是否足够,然后在直接使用顺序表随机访问的特点对栈进行尾插,每次入栈完成我们都需要将top++。
在下面代码中有一个非常精髓的地方,由于我们初始化的时候并没有给数组开辟空间之类的,所以我们巧用了三目运算符来对我们新开辟的空间的大小进行分配,如果是第一次我们就将空间的大小搞成4,之后的过程就是一次扩2倍的空间。
代码如下:
void PushStack(ST* ps, STDataType x)
{
assert(ps);
//先检查空间够不够
if (ps->top == ps->capacity)
{
int newcapcity = (ps->capacity == 0 ? 4 : 2 * ps->capacity);
STDataType* tmp = (STDataType*)realloc(ps->S, sizeof(STDataType) * newcapcity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->S = tmp;
ps->capacity = newcapcity;
}
ps->S[ps->top] = x;
++ps->top;
}3:栈的出栈操作:这里我们需要用暴力的解法先判断栈是否为空,如果为空就给我们报错,不为空才能进行出栈的操作,然后我们的就top--。
代码如下:
void PopStack(ST* ps)
{
assert(ps);
//非空
assert(ps->top > 0);
ps->top--;
}4:栈的获取栈顶元素的操作:首先还是得判断栈是否为空,为空就这个接口就会报错。
在这个代码中我们要注意的是我们栈顶元素得下标并不是top而是top-1
代码如下:
STDataType GetStack(ST*ps)
{
assert(ps);
//非空
assert(ps->top > 0);
return ps->S[ps->top-1];
}5:栈的大小:我们直接返回top就行。
代码如下:
int SizeStack(ST* ps)
{
assert(ps);
return ps->top;
}6:判断栈是否为空:这里如果top为0,则说明栈中无元素返回true,如果有元素返回true,这里要注意c语言中并没有这两个关键字,我们需要引入头文件<stdbool.h>
代码如下:
bool EmptyStack(ST* ps)
{
assert(ps);
//这里代码的意思是如果top为0,则返回真,不为0返回false
return ps->top == 0;
}为了体现栈的特点所以我们在打印出栈中数据的时候,并不是直接遍历数组的
我们使用的是--->
while (!EmptyStack(&st))
{
printf("%d ", GetStack(&st));
PopStack(&st);
}这里是每次取栈顶的元素,然后在删除栈顶的元素。这样才能体现出栈的特点。

图解:
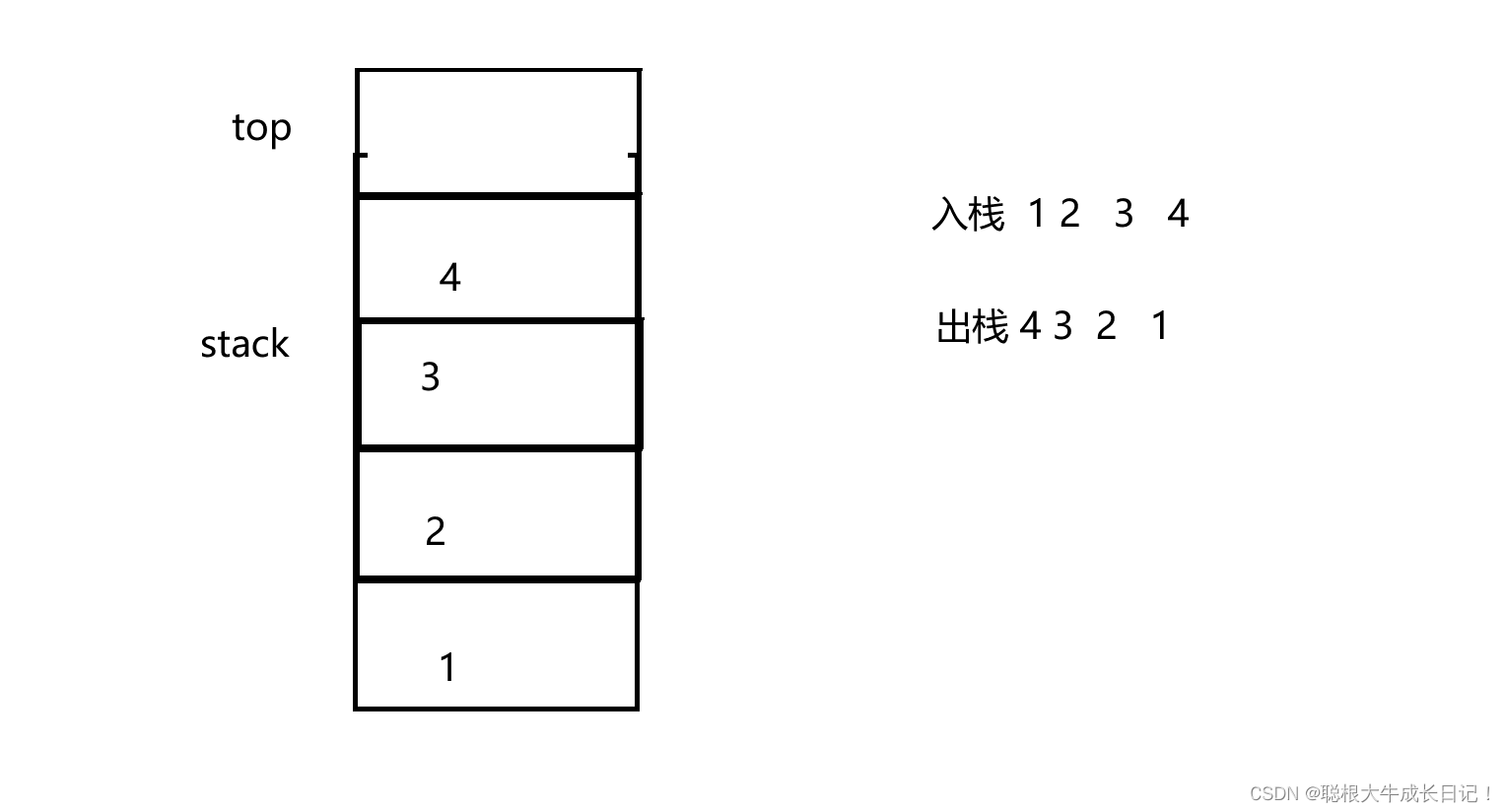
栈的详解就到这里结束了。
1:队列的定义与特点
队列的定义:队列也是一种特殊的线性表,它只能在一端进行插入操作,在另外一端进行删除的操作,我们将插入的一端称为队尾,将删除的一端我们称之为队头,这种结构在我们生活中非常常见,我们可以想象一下我们在食堂排队的情况,如果有人来了那么它就会往队尾进行插入,打完饭的人则会从队头出队。
出队:将队头的元素进行删除的操作
入队:在队尾插入数据的操作。
队列特点:只能在队头进行删除的操作,在队尾进行插入的操作,遵循先进先出的原则。
图:

2:用啥结构来实现队列与原因?
先公布答案:相对与顺序表来说我们一般使用链表来实现队列这一数据结构。
原因:链表在进行头删的时候更加方便,在进行尾插的时候我们只需要定义一个尾指针就可以节省时间了。
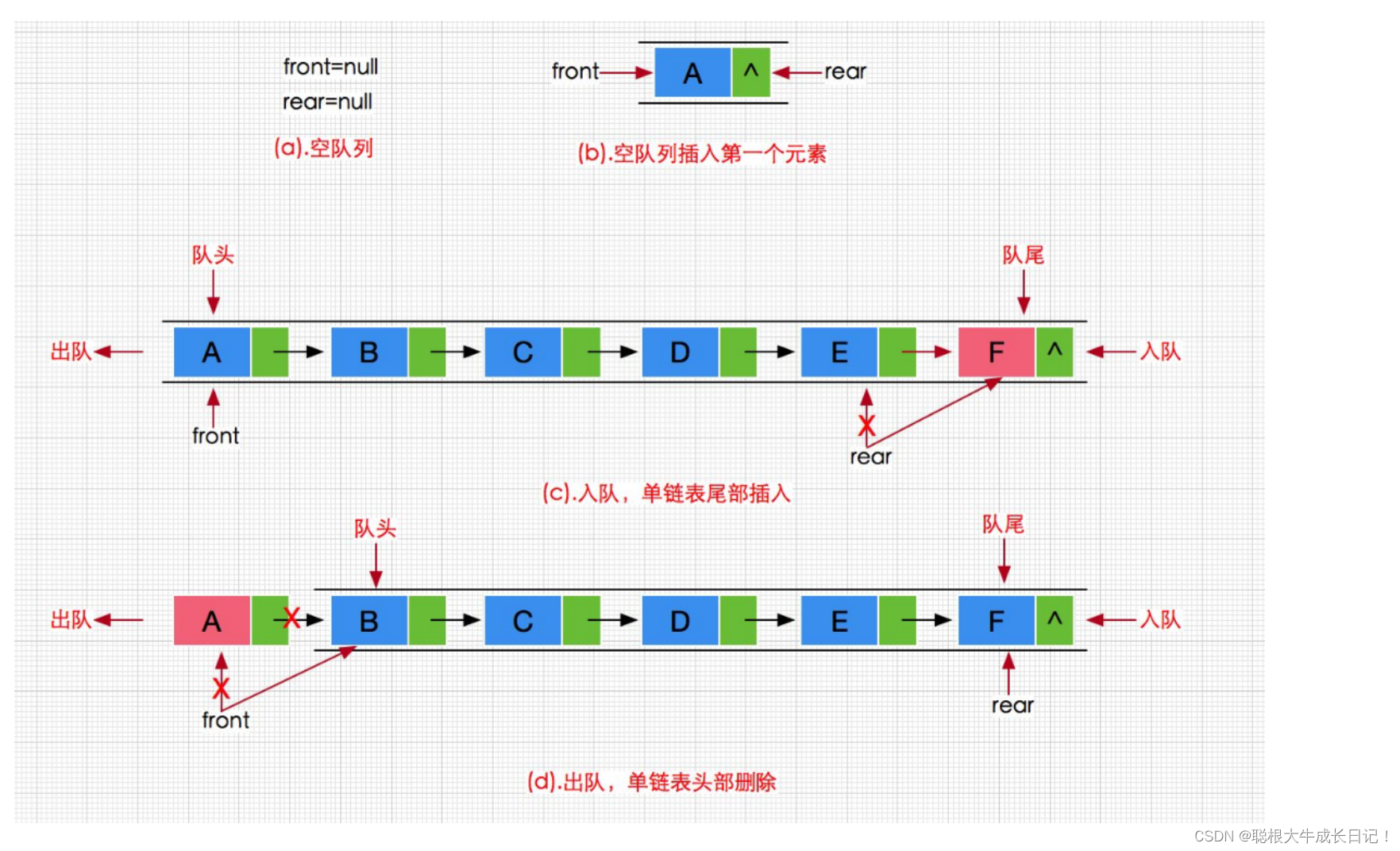
3:(详解)队列的常用接口
队列的接口包括:初始化队列,销毁队列,入队操作,出队操作,判断队列是否为空
获取队头元素,获取队尾元素,判断队列的大小。
首先我们先来了解队列的结构代码分析:
typedef int QueueDataType;
typedef struct QNode
{
struct QNode* next;
QueueDataType data;
}QNode;
typedef struct Queue
{
QNode* head;
QNode* tail;
int size;//用来记录有多少个结点,可以直接算大小
}Que;首先队列的每个元素都是一个链表的基本结构,我们只需要记录链表的头节点与尾结点我们就可以将队列给表示出来,而又因为我们一般传参的时候只传地址所以我们就将头指针与尾指针定义到一个结构体当中,并且增加一个成员变量size,用来记录队列元素的个数。
将两个指针放到同一个结构体中,有一个好处就是我们只需要通过结构体指针就可以改变我们的指针的值,不然就需要使用二级指针来修改它们的值。
 1:队列的初始化:如果你和我的初始化不同那么可能会导致后面一些接口中步骤有些差异。初始化并不唯一
1:队列的初始化:如果你和我的初始化不同那么可能会导致后面一些接口中步骤有些差异。初始化并不唯一
代码如下:
void QueueInit(Que* pq)
{
assert(pq);
pq->head = pq->tail = 0;
pq->size = 0;
}2:入队操作:这里需要分为两种情况,第一张是插入第一个元素的时候我们需要将两个指针的指向给改变,另外一种情况我们只需要在尾指针的后面插入一个新的结点即可,与此同时我们将尾指针指向新结点,插入之后我们的size++;
代码如下:
void QueuePush(Que* pq, QueueDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail:");
exit(-1);
}
//为第一个结点的时候
if (pq->head == NULL)
{
pq->head = pq->tail = newnode;
}
//不是第一个结点
else
{
pq->tail->next = newnode;
}
pq->tail = newnode;
newnode->data = x;
newnode->next = NULL;
pq->size++;
}
3:出队操作:首先得判断队列中是否含有数据元素,且有两类,一类是队列中只有一个元素,那么我们需要将这个元素删除,并且将head与tail的值置为空,在size--;
代码如下:
void QueuePop(Que* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
//只有一个结点的时候
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* phead = pq->head->next;
free(pq->head);
pq->head = phead;
}
pq->size--;4:获取队头元素:这个非常简单,先判断队列是否为空,不为空我们只需要返回head->data,就行。
代码如下:
QueueDataType QueueFront(Que* pq)
{
assert(pq);//判断pq是否有意义
assert(!QueueEmpty(pq));
return pq->head->data;
}
5:获取队尾元素:与上面的思路类似,只需要返回tail指针所指向的数据元素就行
QueueDataType QueueBack(Que* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
6:判断队列是否为空:为空那么head指针就为空,head为NULL则返回true,否则返回false
代码如下:
bool QueueEmpty(Que* pq)
{
assert(pq);
return pq->head==NULL;
}7:队列的元素个数判断:我们根据我们所定义的结构可在,我们只需要返回size即可。
int QueueSize(Que* pq)
{
assert(pq);
return pq->size;
} 在某种情况下可以使用栈转化为队列,也可以使用队列转化为栈,让我们一起想一想它是如何转化的吧。
!!!本章完,感谢大家的耐心观看!