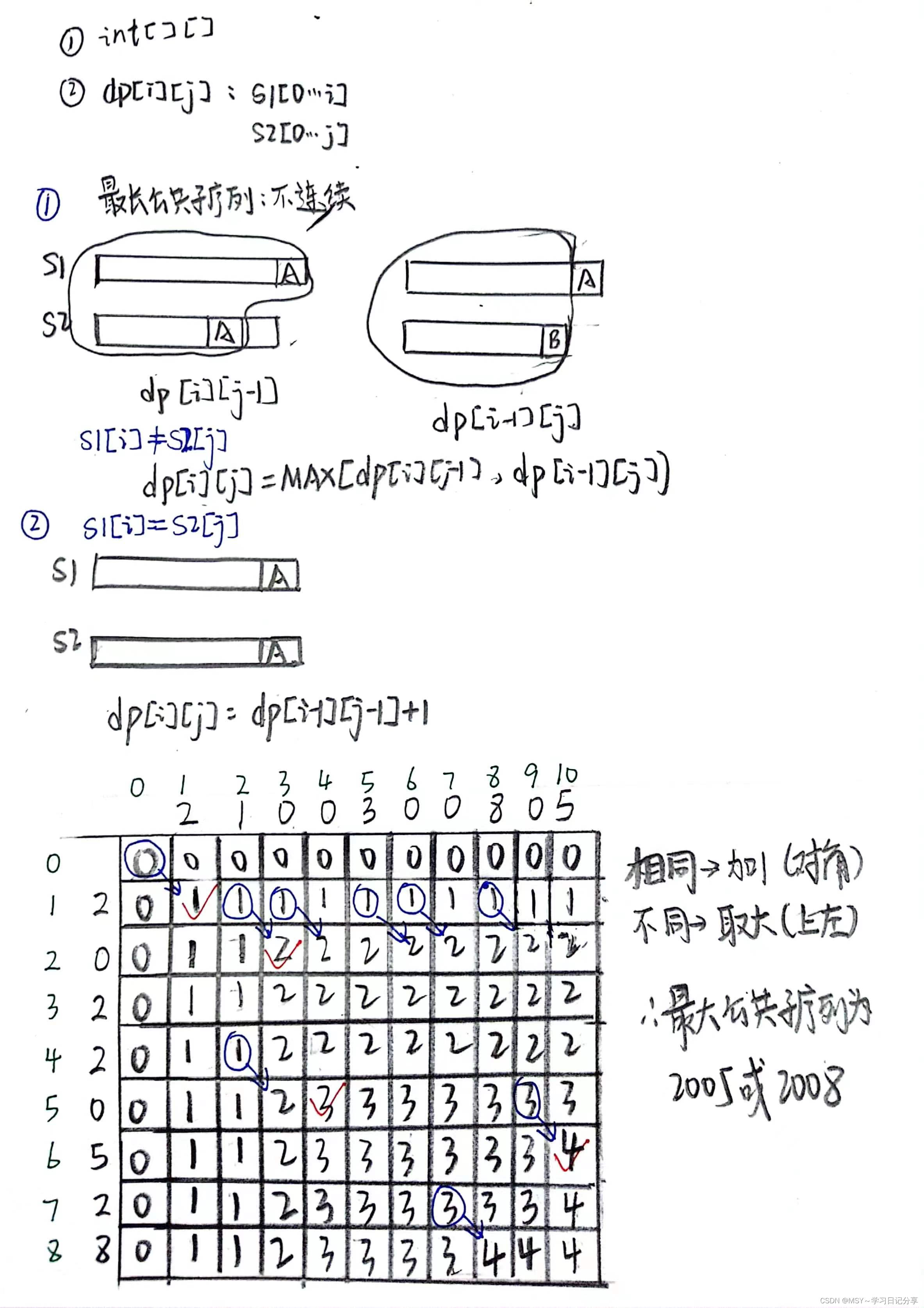
每日一题 823. 带因子的二叉树 难度：中等

思路：

1. 取乘积，那么两个叶子节点相乘一定会得到一个更大的数，所以先排序
2. 以父节点为根节点的数的数量 = 以右节点为根节点的数的数量 * 以左节点为根节点的数的数量
3. 初始化列表，每个数作为根节点都至少能以它本身构建一棵树，所以每个数的初始对应数量为 1，这里为了快速查找，定义字典来实现
4. 从小到大遍历排好序的数组，寻找能构成 右子 * 左子 = 当前数 的组合，并更新当前数所对应的组合数
5. 返回字典中所有值的和

代码如下：

class Solution:
    def numFactoredBinaryTrees(self, arr: List[int]) -> int:
        arr.sort()
        t = {}
        for i in range(len(arr)):
            t[arr[i]] = 1
        for i in range(len(arr)):
            for j in range(0, i):
                if arr[i] % arr[j] == 0 and arr[i]/arr[j] in t:
                    t[arr[i]] = (t[arr[i]] + t[arr[j]] * t[arr[i]/arr[j]]) % (10 ** 9 + 7)
        return sum(t.values()) % (10 ** 9 + 7)

但我不知道为什么下面的代码能更快实现，感觉差不多
学习：快速构建含有初值的字典 r = { x: 1 for x in arr}

class Solution: 
    def numFactoredBinaryTrees(self, arr: List[int]) -> int:
        arr.sort()
        r = { x: 1 for x in arr}
        for x in arr:
            a = sqrt(x)
            if a in r:
                r[x] += r[a] ** 2
            for j in range(bisect.bisect_left(arr, a)):
                if not x % arr[j] and x / arr[j] in r:
                    r[x] += r[arr[j]] * r[x / arr[j]] * 2
        return sum(r.values()) % 1000000007