https://zhuanlan.zhihu.com/p/158705342
概念
单目标优化只有一个优化目标,所以可以比较其好坏。
但是多目标优化,在需要优化多个目标时,容易存在目标之间的冲突,一个目标的优化是以其他目标劣化为代价的,所以我们要进行协调和折中。
发展
帕累托模型、进化算法、多目标蚁群算法、多目标遗传算法、多目标粒子群算法、多目标优化算法
常用解法
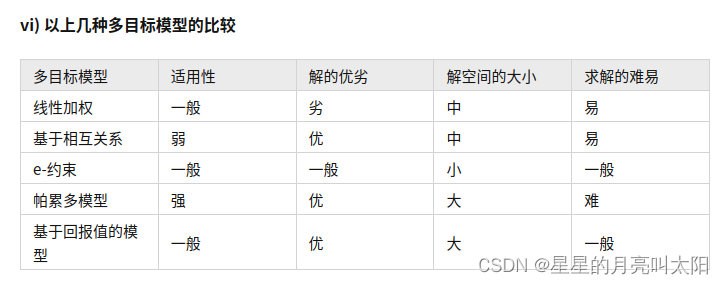
线性加权
它忽略不同目标函数有不同的单位和范围,通过给不同的目标函数制定相应的权重,将所有的目标函数进行线性加权,用一个综合的效用函数来代表总体优化的目标.最优的效用函数对应的解即被认为是问题的最优解,从而将多目标优化问题转化成单目标优化问题。

主要分为两个步骤:缩放和制定权重。
缩放过程统一将各个目标函数从它们的原始值缩放,或和目标函数的最大值、最小值比较,或和目标函数的平均值比较.如针对目标函数 f(x),已知它的最大值是fmax,最小值是fmin ,采用的缩放方式如下图式

优点:简单 实现起来容易,求解容易
** 缺点** : 刻画目标和解还不够精细,失去了一定的目标原始信息。另外缩放过程需要提前知道最大最小值等。
应用领域主要是应用在多个目标在相互独立的时候。
基于相互关系
下面公式考虑了两个目标之间的相互关系,物理意义?

Pareto
著名的帕累托优化(Pareto Optimum)理论: “只有当一个目标不得不以牺牲其他目标为条件进行优化,一个社会才达到了资源分配的最优化。”帕累托(Pareto)是多目标优化中经典的模型,并且它完全基于原始数据,没有将问题转化成单 目标问题分析。
帕累托模型由于不需要对目标进行缩放和归一化,也不需要设定或者引入新的参数、变量(如权重、界限值),直接基于原始目标函数和值进行操作,可以适用于任何目标、任何函数.它不会丢失目标函数和解的信息,解的优劣可以较好保证.但帕累托模型的最优解是一个集合,其中包含不止一个最优解,因此要穷尽并求出所有的帕累托最优解有一定的难度.
基于回报值
基于回报值的优化模型旨在深入刻画优化的本质需求,将评价指标转化为回报值,描述系统或服务的指标属性对优化目标的作用,针对需求进行更为合理、有效的优化.基于回报值的优化往往结合性能评价同时开展.在优化过程中,研究不同评价指标对求解目标的本质影响,形式化刻画评价指标与回报值的量化关系,给出转化公式;随后将回报值进行叠加,得到最终的优化函数由于回报值可以精确量化表达,因而该优化模型可以得到理论最优解.但是,大规模服务计算中的状态空间很大,同时考虑到决策行为的多样性,基于回报值的优化模型可能会遇到状态爆炸问题,需要通过状态合并、近似分析等技术手段加以克服。
例如,在考虑服务过程时,回报值可以定义为服务的利润,即收益减开销
e-约束
参考下一篇