- 相关概念
- 树的表示
- 二叉树
- 二叉树性质
- 二叉树储存
- 实现一颗二叉树
- 创建
- 遍历(前中后序)
- 获取树中节点个数
- 获取叶子节点个数
- 获取第k层节点个数
- 获取二叉树高度
- 检测值为value元素是否存在
- 层序遍历(需要队列来实现)
- 判断是否为完全二叉树(需要队列来实现)
相关概念
重点概念:后续学习将会反反复复出现

对我们当前学习稍微不重要:

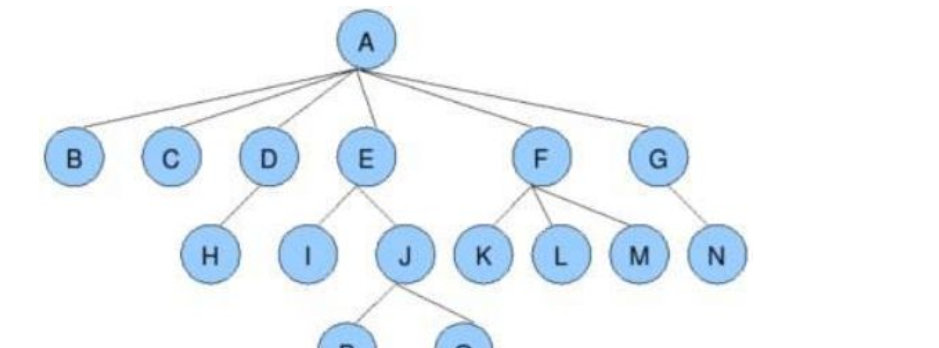
树的表示
树有很多种表示方式,如:双亲表示法,孩子表示法、孩子双亲表示法(AVL树、红黑树、B树会用到)、孩子兄弟表示法等等。我们了解一下孩子兄弟表示法:
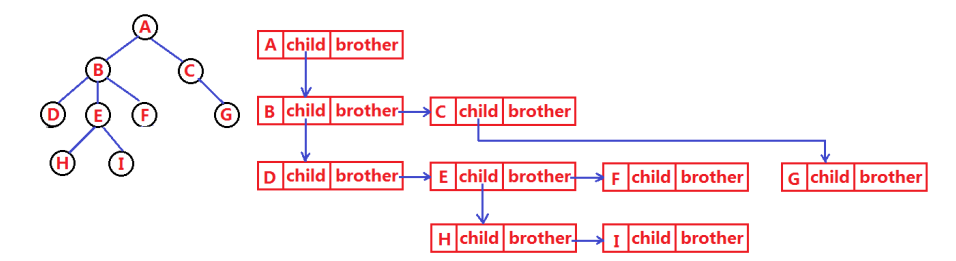
代码表示:
class Node{
int value;//我们当前学习就是简简单单的存个int数字
Node firstChild;
Node nextNorther;
}
二叉树
二叉树:每一个节点的度小于等于2;其实就是每一个节点的孩子个数不超过两个。二叉树的有次序是指你把右子树放左边画出来,结果就是两个不同的树
任意二叉树都是由以下的情况组合的:
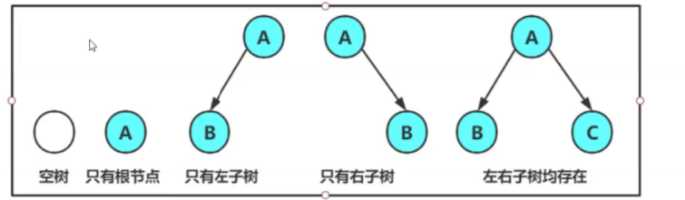
满二叉树:每层的结点数都达到最大值;如果层数是k;满二叉树的节点个数为2^k-1
完全二叉树:你按左右到上下编号1-n一定是连续的
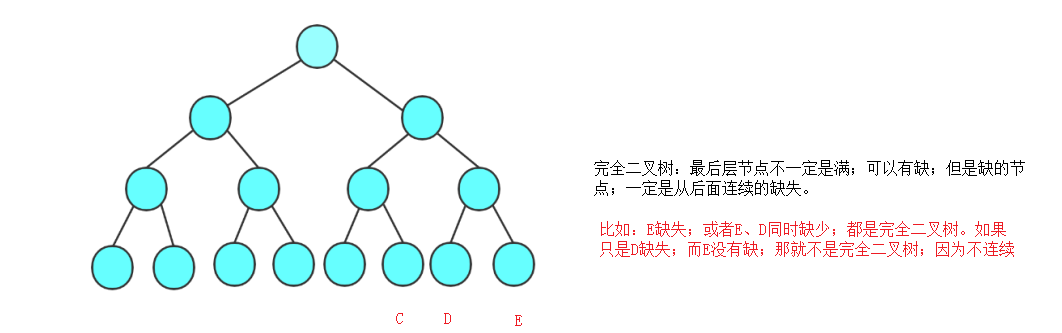
二叉树性质
前提:规定第一层是根节点的二叉树
1:第i层最多节点个数:2^(i-1)
2:深度为k;总节点个数最多是2^k-1 (完全二叉树的情况)
3:非常重要;任意的二叉树;叶子节点个数比度为2的节点个数多一个(度为0就是叶子,不涉及到度为1的节点)
n0=n2+1 (如果要把n1也扯上关系;使用n-1=n00+n11+n2*2;n是总节点个数;解释:一颗n个节点的树有N-1条边;而叶子节点不产生边;度为1的节点只产生一条边;度为2的节点产生两条边)
比如有4层:
其实就是;2的4次方等于2的3次方+2都平方+2的1次方+2的0次方+1。
题目:
某二叉树共有399个结点,其中有199个度为2的结点,则该二叉树中的叶子结点数为()
A不存在这样的二叉树
B200
C198
D199
4:具有n个结点的完全二叉树的深度k为log(n+1)向上取整
不受到你最后层节点个数影响,最后层一个跟2的n-1个是一样,因为用最大节点个数推导出来的
5:对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点若2i+1<n,左孩子序号:2i+1,否则无左孩子
若2i+2<n,右孩子序号:2i+2,否则无右孩子
注意:完全二叉树度为1的节点要么是1个,要么是0个。奇数个节点就没有度为1的节点,偶数个节点就有一个度为1的节点。如果题目告诉你2n个节点;那就说明有度为1的节点
二叉树储存

如何遍历:
先序:根—>左子树---->右子树(这个比较容易理解)
中序:左子树—>根—>右子树(先访问左子树,然后你左子树又得按照中序进行)
后序:左子树–>右子树—>根
实现一颗二叉树
创建
//创建一颗树
class tree{
//树的节点,还是内部类实现,类似链表
class Listnode{
//一个节点包含三个域
char val;
Listnode left;//左边
Listnode right;//右边
public Listnode(char val) {
this.val = val;
}
}
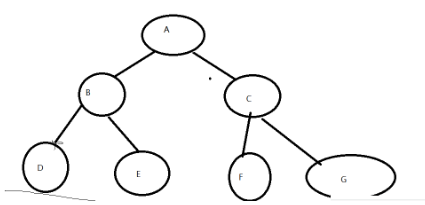
public Listnode create(){
//先把节点和值创建好,然后再绑关系
Listnode A=new Listnode('A');
Listnode B=new Listnode('B');
Listnode C=new Listnode('C');
Listnode D=new Listnode('D');
Listnode E=new Listnode('E');
Listnode F=new Listnode('F');
Listnode G=new Listnode('G');
//这里的B和C是节点
A.left=B;
A.right=C;
B.left=D;
B.right=E;
C.left=F;
C.right=G;
return A;//返回根节点
}
遍历(前中后序)
前序:
public void print1(Listnode root){
if(root==null) {
return ;
}
System.out.println(root.val);
print1(root.left);
print1(root.right);
}
中序:这次我们就不打印;遍历把值存在顺序表里
public List<Character> print2(Listnode root){
List<Character> list=new ArrayList<>();
if(root==null)
{
return list;
}
//System.out.println(root.val);
list.add(root.val);
print2(root.left);
print2(root.right);
return list;
}
后序:
public List<Character> print3(Listnode root){
List<Character> ret=new ArrayList<>();
if(root==null)
{
return ret;
}
//System.out.println(root.val);
ret.add(root.val);//先把头放进去,然后左边放一个表,右边放一个表,最后放到ret
List<Character> s=print3(root.left);
ret.addAll(s);
List<Character> s1=print3(root.right);
ret.addAll(s1);
return ret;
}
获取树中节点个数
//获取树中节点的个数
int num=0;
public int size(Listnode root){
//遍历计数器
if(root==null) {
return 0;
}
num++;
size(root.left);
size(root.right);
return num;
}
//子问题计数
public int size1(Listnode root){
if(root==null) {
return 0;
}
int tmp =size1(root.left)+size1(root.right)+1;//(把走到每个节点都分为左边、右边和它自己)
return tmp;
}
获取叶子节点个数
// 获取叶子节点的个数
int ret3=0;
public void getLeafNodeCount(Listnode root){
//自己为空,肯定就结束了
if(root==null){
return ;
}
//如果左边和右边同时为空就计数
if(root.left==null&&root.right==null){
ret3++;
}
getLeafNodeCount(root.left);
getLeafNodeCount(root.right);
}
// 子问题思路-求叶子结点个数
public int getLeafNodeCount1(Listnode root){
//自己为空,肯定就结束了
if(root==null){
return 0;
}
//如果左边和右边同时为空就计数
if(root.left==null&&root.right==null){
return 1;
}
return getLeafNodeCount1(root.left)+getLeafNodeCount1(root.right);
}
获取第k层节点个数
// 获取第K层节点的个数,直接子问题
public int getKLevelNodeCount(Listnode root,int k){
//我们之前不是求了一棵树节点个数吗;假设我要求k层,在k-1的左右子树的和
if(root==null||k<=0) {
return -1;
}
if(k==1){//这时候条件就不再是root.left==null&&root.right==null;而是k-1层的孩子节点我都要计算
return 1;
}
int tmp=getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);
return tmp;
}
获取二叉树高度
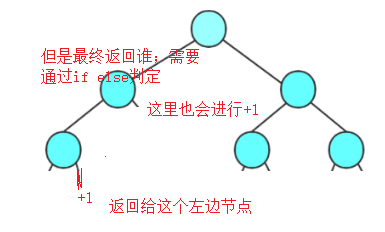
非常巧妙:递归的结束root==null;返回上一级到叶子节点;发现height1>height2不成立;叶子节点的右边+1;如果是root.left遍历下的就返回给这里的值。画个图就好理解
// 获取二叉树的高度
public int getHeight(Listnode root) {
if(root==null){
return 0;
}
int height1= getHeight(root.left);
int height2= getHeight(root.right);
if (height1>height2){
return height1+1;//加1是关键,每结束一层+1
}
else
return height2+1;
}
检测值为value元素是否存在
// 检测值为value的元素是否存在
public Listnode find(Listnode root, int val) {
if (root == null) {
return null;
}
if (root.val == val) {
return root;
}
find(root.left, val);//这里应该把find(root.left,val)存到ret里,避免下面用这个又要重复再递归一次
if (find(root.left, val).val == val) {
return root;
} //如果我在左边找到就不去右边
//如果我在右边找到就直接结束,如果都没找到
find(root.right, val);
if (find(root.right, val).val == val) {
return root;
}
return null;
}
层序遍历(需要队列来实现)
因为二叉树;没法按这种顺序来遍历;就得依靠别的数据结构

这样子它的打印顺序就是从左到右;画图分析好
判断是否为完全二叉树(需要队列来实现)
队列;逻辑:按层次遍历弹出,把Null也放入队列里,当弹出Null的时候发现队列全为Null,就说明是完全二叉树
。不全为null就不是完全二叉树。
// 判断一棵树是不是完全二叉树 ,这题逻辑还是非常清晰
public boolean isCompleteTree(TreeNode root) {
if(root == null) {
return true;
}
Queue<TreeNode> qu = new LinkedList<>();
qu.offer(root);
while (!qu.isEmpty()) {
TreeNode cur = qu.poll();
if(cur != null) {
qu.offer(cur.left);
qu.offer(cur.right);
}else {
break;
}
}
//判断队列剩下的值 是否有 非null的数据
while (!qu.isEmpty()) {
TreeNode pop = qu.poll();
if(pop != null) {
return false;
}
}
return true;
}