0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

1 A*算法的局限性

A*算法的局限性在于其搜索路径的可行角度被网格形状固定。因此，A* 算法搜索的路径往往不是实际地形下真正的最短路径(由8邻域二维栅格边缘形成的最短路径可能比连续环境中真实的最短路径长多达8%)，如图所示。

在这里插入图片描述

Theta*算法的核心原理是去除依赖于网格形状的角度约束，不限制路径仅由栅格边缘组成，以提升路径平滑性和最优性

2 Theta*算法原理图解

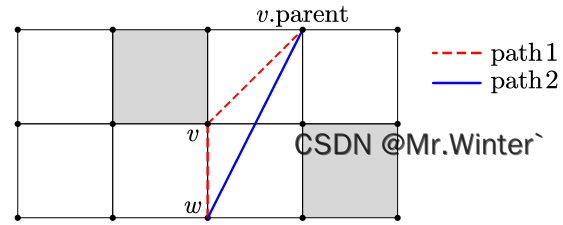
Theta*算法主体流程与A*相同，区别在于扩展节点数据的更新方式。

A*算法利用邻接节点更新信息(path1)，即若 $g\left( w \right) >g\left( v \right) +\mathrm{d}\left( v,w \right)$ ，则令 $g\left( w \right) =g\left( v \right) +\mathrm{d}\left( v,w \right)$
Theta*额外考虑当前节点的父节点信息(path2)，即若 $g\left( w \right) >g\left( v.\mathrm{parent} \right) +\mathrm{d}\left( v.\mathrm{parent},w \right)$ ，则令 $g\left( w \right) =g\left( v.\mathrm{parent} \right) +\mathrm{d}\left( v.\mathrm{parent},w \right)$ 。

根据三角形两边之和大于第三边有

$\mathrm{d}\left( v.\mathrm{parent},w \right) <\mathrm{d}\left( v.\mathrm{parent},v \right) +\mathrm{d}\left( v,w \right)$

因此当 $v.\mathrm{parent}$ 与 $w$ 间不存在障碍物时，算法必然采用path2，实现锯齿路径的平滑

在这里插入图片描述

3 Bresenham视线法

在Theta*中，对障碍物的碰撞检测采用Bresenham算法。Bresenham碰撞测试在三种类型的移动中访问单元格：

$x$ 方向移动
$y$ 方向移动
对角线移动

在栅格地图中，碰撞检测点连线经过若干离散栅格，因此每次移动都将产生非连续误差，Bresenham算法要求下一个移动偏差最小。通过迭代即可访问检测线经过的所有栅格，判断这些栅格的代价是否超过阈值即可完成碰撞检测。

算法流程如下所示

在这里插入图片描述

4 算法仿真测试

4.1 算法流程图

算法流程与核心函数如下所示

在这里插入图片描述

4.2 ROS C++ 实现

核心代码如下

bool ThetaStar::plan(const unsigned char* global_costmap, const Node& start, const Node& goal, std::vector<Node>& path,
                     std::vector<Node>& expand)
{
  // initialize
  costs_ = global_costmap;
  path.clear();
  expand.clear();

  // open list and closed list
  std::priority_queue<Node, std::vector<Node>, compare_cost> open_list;
  std::unordered_set<Node, NodeIdAsHash, compare_coordinates> closed_list;

  open_list.push(start);

  // get all possible motions
  const std::vector<Node> motion = getMotion();

  // main process
  while (!open_list.empty())
  {
    // pop current node from open list
    Node current = open_list.top();
    open_list.pop();

    // current node does not exist in closed list
    if (closed_list.find(current) != closed_list.end())
      continue;

    closed_list.insert(current);
    expand.push_back(current);

    // goal found
    if (current == goal)
    {
      path = _convertClosedListToPath(closed_list, start, goal);
      return true;
    }

    // explore neighbor of current node
    for (const auto& m : motion)
    {
      Node node_new = current + m;  // add the x_, y_, g_

      // current node do not exist in closed list
      if (closed_list.find(node_new) != closed_list.end())
        continue;

      // explore a new node
      // path 1
      node_new.h_ = dist(node_new, goal);
      node_new.id_ = grid2Index(node_new.x_, node_new.y_);
      node_new.pid_ = current.id_;

      // next node hit the boundary or obstacle
      if ((node_new.id_ < 0) || (node_new.id_ >= ns_) || (costs_[node_new.id_] >= lethal_cost_ * factor_))
        continue;

      // get the coordinate of parent node
      Node parent;
      parent.id_ = current.pid_;
      index2Grid(parent.id_, parent.x_, parent.y_);

      // update g value
      auto find_parent = closed_list.find(parent);
      if (find_parent != closed_list.end())
      {
        parent = *find_parent;
        _updateVertex(parent, node_new);
      }

      open_list.push(node_new);
    }
  }

  return false;
}

效果如下

在这里插入图片描述

4.3 Python实现

核心代码如下

def plan(self):
	# OPEN set with priority and CLOSED set
	OPEN = []
	heapq.heappush(OPEN, self.start)
	CLOSED = []
	
	while OPEN:
	    node = heapq.heappop(OPEN)
	
	    # exists in CLOSED set
	    if node in CLOSED:
	        continue
	
	    # goal found
	    if node == self.goal:
	        CLOSED.append(node)
	        return self.extractPath(CLOSED), CLOSED
	
	    for node_n in self.getNeighbor(node):                
	        # exists in CLOSED set
	        if node_n in CLOSED:
	            continue
	        
	        # path1
	        node_n.parent = node.current
	        node_n.h = self.h(node_n, self.goal)
	
	        try:
	            p_index = CLOSED.index(Node(node.parent))
	            node_p = CLOSED[p_index]
	        except:
	            node_p = None
	
	        if node_p:
	            self.updateVertex(node_p, node_n)
	
	        # goal found
	        if node_n == self.goal:
	            heapq.heappush(OPEN, node_n)
	            break
	        
	        # update OPEN set
	        heapq.heappush(OPEN, node_n)
	    
	    CLOSED.append(node)
	return ([], []), []

效果如下

在这里插入图片描述

4.4 Matlab实现

核心代码如下

while ~isempty(OPEN)
    % pop
    f = OPEN(:, 3) + OPEN(:, 4);
    [~, index] = min(f);
    cur_node = OPEN(index, :);
    OPEN(index, :) = [];

    % exists in CLOSED set
    if loc_list(cur_node, CLOSED, [1, 2])
        continue
    end

    % update expand zone
    if ~loc_list(cur_node, EXPAND, [1, 2])
        EXPAND = [EXPAND; cur_node(1:2)];
    end

    % goal found
    if cur_node(1) == goal(1) && cur_node(2) == goal(2)
        CLOSED = [cur_node; CLOSED];
        goal_reached = true;
        cost = cur_node(3);
        break
    end
    if (cur_node(1) ==17) &&(cur_node(2) == 26)
        cur_node(1);
    end
    % explore neighbors
    for i = 1:motion_num
        % path 1
        node_n = [
            cur_node(1) + motion(i, 1), ...
            cur_node(2) + motion(i, 2), ...
            cur_node(3) + motion(i, 3), ...
            0, ...
            cur_node(1), cur_node(2)];
        node_n(4) = h(node_n(1:2), goal);

        % exists in CLOSED set
        if loc_list(node_n, CLOSED, [1, 2])
            continue
        end

        % obstacle
        if map(node_n(1), node_n(2)) == 2
            continue
        end

        p_index = loc_list(cur_node(5: 6), CLOSED, [1, 2]);
        if p_index
            node_p = CLOSED(p_index, :);
        else
            node_p = 0;
        end
        
        if node_p ~= 0
            node_n = update_vertex(map, node_p, node_n);
        end
        
        % update OPEN set
        OPEN = [OPEN; node_n];
    end
    CLOSED = [cur_node; CLOSED];