目录
一、基础概念
1. 时域
2. 频域
3. Fourier分析=级数+变换
Fourier级数
Fourier变换
离散谱
连续谱
4. 欧拉公式！！！
欧拉恒等式
二 、三角函数系及Fourier级数
1. 三角函数系
概念
性质——周期性、正交性、完备性
Fourier系数
Fourier级数
黎曼-勒贝格引理
Lp空间
2. Fourier级数的收敛性
Dirichlet核
Riemann局部化定理
定理: Dini判别法
积分第二中值定理
3. Fourier 级数的发散及Lebesgue常数
Fourier 级数的发散
Lebesgue常数
4. 在间断点附近的性质----Gibbs现象！！！
5. L^2中函数的Fourier级数
Bessel不等式
三、Fourier变换与Fourier积分
1. 定义与基本性质 编辑
2. Fourier变换的反演理论
3. 求和理论
4. L^2中函数的Fourier变换
5. 卷积及其Fourier变换
参考文章
傅里叶变换的核心是从时域到频域的变换，而这种变换是通过一组特殊的正交基来实现的.
而贯穿时域与频域的方法之一，就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数（Fourier Serie）和傅里叶变换(Fourier Transformation)。
一、基础概念
1. 时域
时域是描述一个数学函数或物理信号对时间的关系，这也是我们日常中最容易直观感受的一种域。从我们学物理开始，很多物理量的定义都是跟时间相关的。
- 速度：位移与发生这个位移所用的时间之比
- 电流：单位时间里通过导体任一横截面的电量
- 功率：物体在单位时间内所做的功的多少
很多物理量的定义都是基于单位时间产生的效果或者变化，以时间为参考让我们更容易理解。但是容易理解不代表方便使用，或者说方便计算。
2. 频域
频域就是描述频率所用到的空间或者说坐标系。频率虽然比较抽象，但是在我们的生活中是无处不在的，只是我们很少直接提到这个专业名词。
对于波来说，频率是每秒波形重复的数量。声音是一种波；光具有波粒二象性，也具有电磁波的性质；更普遍的说，频率是物质每秒钟完成周期性变化的次数。比如家里用的交流电是50Hz，意思就是电压每秒完成50次振荡周期。
3. Fourier分析=级数+变换
- Fourier级数：在时域是一个周期且连续的函数，而在频域是一个非周期离散的函数。
- Fourier变换：则是将一个时域非周期的连续信号，转换为一个在频域非周期的连续信号
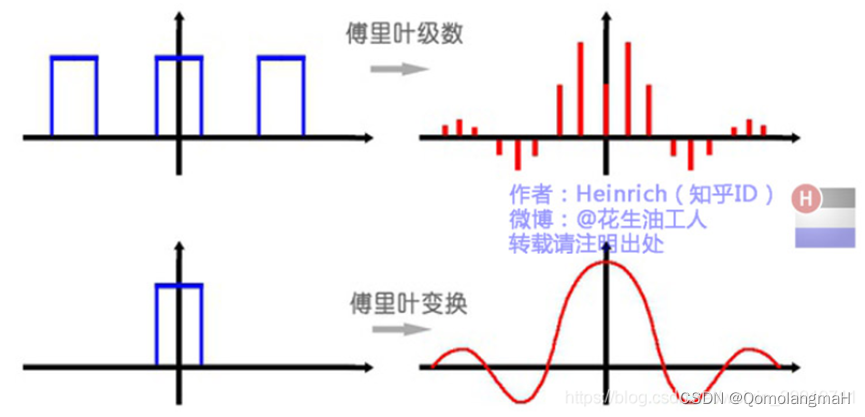
Fourier级数
傅里叶级数的本质是将一个周期的信号分解成无限多分开的（离散的）正弦波
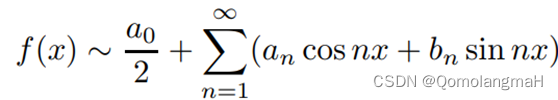
Fourier变换
傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换
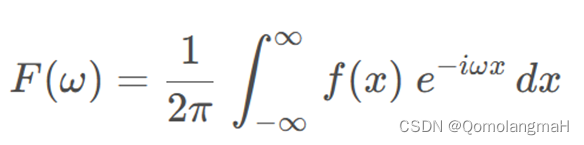
我们称
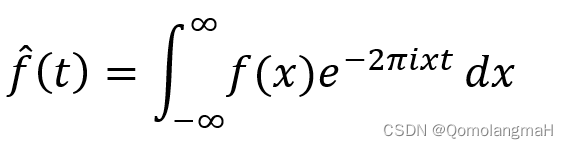
为f的Fourier变换.同时记
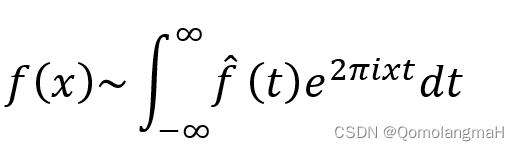
上式右端的积分称为f的Fourier积分.
离散谱
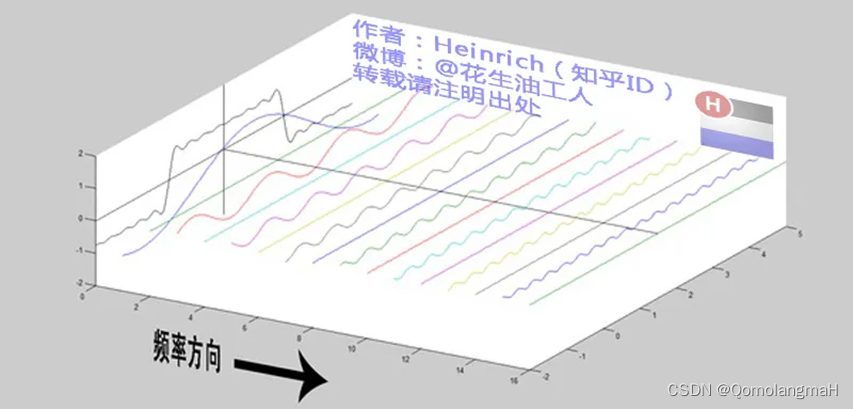
连续谱
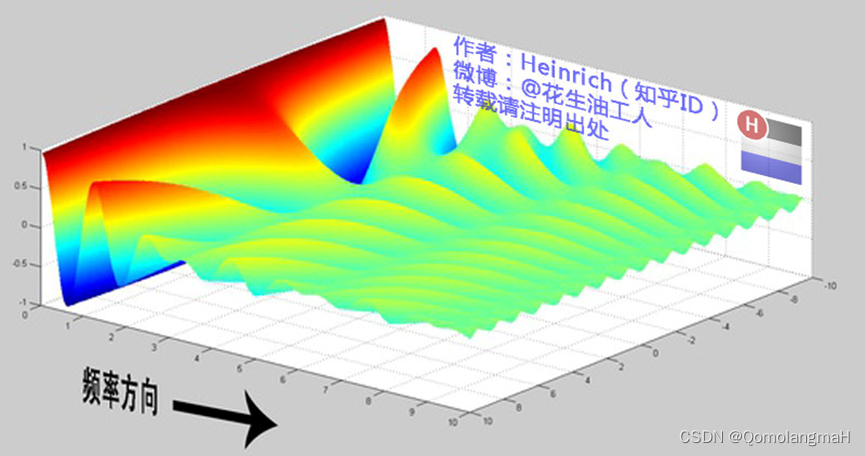
离散谱的叠加，变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号
4. 欧拉公式！！！
欧拉恒等式
二 、三角函数系及Fourier级数
1. 三角函数系
概念
性质——周期性、正交性、完备性
- 周期性：每个函数的周期都是2π
- 正交性：它们在长度为2π 的任意区间上组成正交系,即
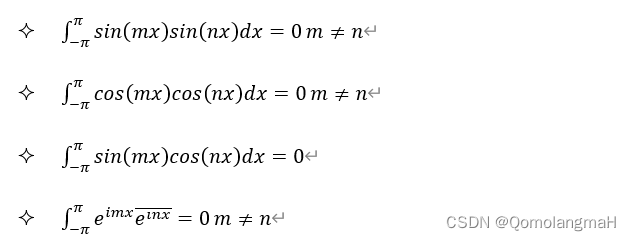
- 完备性：若有𝑓(𝑥)∈L[-𝜋,𝜋]与三角函数系的每一个函数都正交，则𝑓(𝑥)=0
Fourier系数
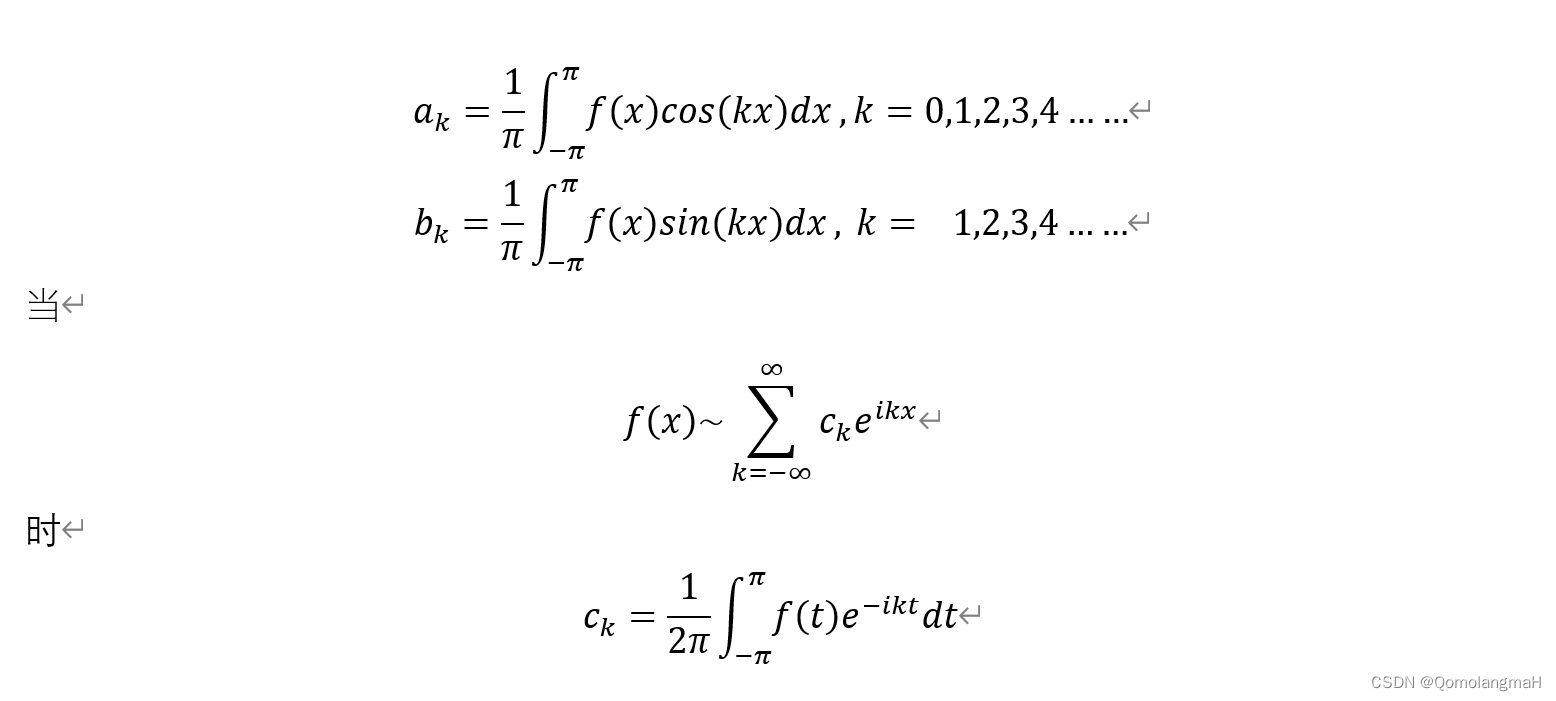
Fourier级数
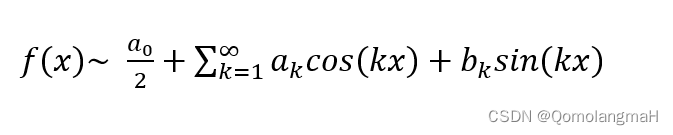
黎曼-勒贝格引理
黎曼-勒贝格引理_百度百科 (baidu.com)
https://baike.baidu.com/item/%E9%BB%8E%E6%9B%BC-%E5%8B%92%E8%B4%9D%E6%A0%BC%E5%BC%95%E7%90%86/23140234
Lp空间
在数学中， L空间是由p次可积函数组成的空间；对应的L空间是由p次可和序列组成的空间
在泛函分析和拓扑向量空间中，他们构成了Banach空间一类重要的例子。L空间都是巴拿赫空间，但只有当p=2的时候，L空间是希尔伯特空间。也就是说，可以为L空间中的元素定义内积。
2. Fourier级数的收敛性
Dirichlet核
Riemann局部化定理
定理: Dini判别法
积分第二中值定理
怎样比较直观的理解积分第二中值定理？感觉教科书上的不太好理解 - 知乎 (zhihu.com)https://www.zhihu.com/question/46040259
3. Fourier 级数的发散及Lebesgue常数
Fourier 级数的发散
Lebesgue常数
4. 在间断点附近的性质----Gibbs现象！！！
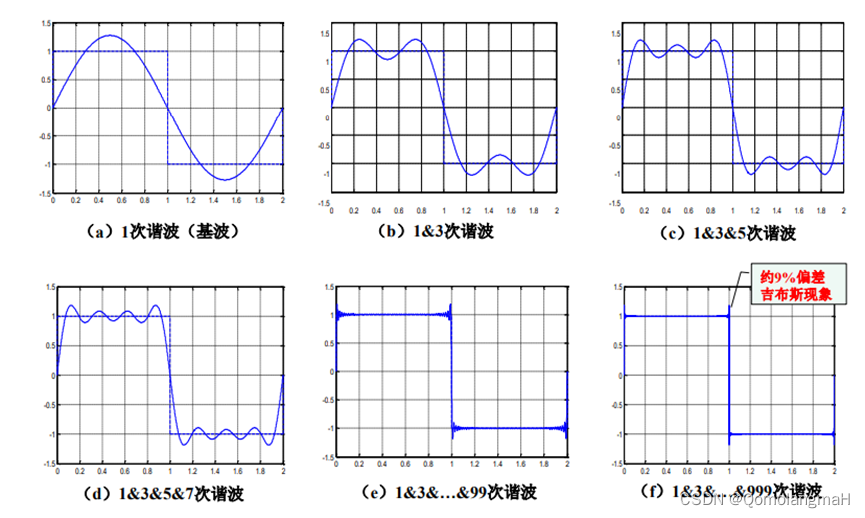
若有界变差的周期函数f(x)有间断点x0 ，则f的 Fourier级数在任意包含x0的小区间上不可能一致收敛.
因为 Fourier级数的部分和总是连续的，而连续函数列一致收敛的极限也是连续的.19世纪末年，J.W. Gibbs在回答一位物理学家对于有间断点的函数f用连续函数Sn（f,x）来代替所产生的疑问时，指出了这种一不致收敛的缺点，此后，关于 Fourier级数在函数f的间断点附近出现的这类现象就称为 Gibbs现象。
5. 
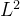中函数的Fourier级数
Bessel不等式
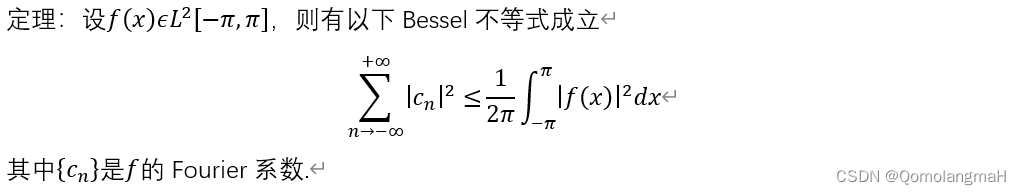
三、Fourier变换与Fourier积分
我们知道，在各种问题中常出现定义在实轴上的非周期函数，这些函数无法周期化，从而不可能展成Fourier级数.但是，我们仍希望能用一些基本的函数，如指数函数或三角函数，通过迭加来表示它们，也就是想得到它们的展开式.这时的展开式不可能是离散形式的和式，而只能是连续形式的和式，也就是积分。
1. 定义与基本性质 
以下内容待补充
2. Fourier变换的反演理论
3. 求和理论
4. L^2中函数的Fourier变换
5. 卷积及其Fourier变换
本文介绍了基于Fourier分析的信号处理中的基础概念和理论。首先介绍了时域、频域的概念，并解释了Fourier分析是将信号表示为级数或变换的方法。接下来，介绍了三角函数系的概念、周期性、正交性和完备性等性质，并讨论了Fourier级数的收敛性和发散性。文章还涉及到了Gibbs现象和L^2空间中函数的Fourier级数。最后，介绍了Fourier变换的定义和基本性质，包括反演理论、求和理论以及卷积和Fourier变换之间的关系。
参考文章
部分内容参考：
傅里叶分析之掐死教程（完整版）更新于2014.06.06 - 知乎作 者：韩 昊 知 乎：Heinrich 微 博：@花生油工人 知乎专栏：与时间无关的故事 谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。 转载的同学请保留上面这句话，谢谢。如果还能保留文…
https://zhuanlan.zhihu.com/p/19763358
