文章目录
- 1. 前言
- 2. 固定长度编码
- 3. 哈夫曼编码
- 4. 哈夫曼解码
- 5. 编码特点
- 6. 代码实现
- 7. 总结
1. 前言
在上一篇文章中,介绍了 哈夫曼树的概念及其实现 。
哈夫曼树有什么用途呢? —— 那就是用来创建哈夫曼编码(Huffman Coding —— 一种二进制编码)。
哈夫曼编码是一种可以用于数据压缩的编码方式,比如你可以想象在 winrar 或 winzip 等压缩软件中采用这种压缩方式。而哈夫曼编码的构造过程是需要用到哈夫曼树。
2. 固定长度编码
哈夫曼编码主要解决通信双方传输信息时针对信息压缩问题,通过传输最少量的信息来表达一段相同的内容。
设想有一段文字内容 “AFDBCFBDEFDF” 要通过网络传给别人。
一般来说,传输一段信息时,往往采用二进制的 0 和 1(分别代表两种信号)来进行信息传输最便捷,所以考虑把要传输的这段文字内容进行编码。
因为这段文字内容只涉及了 A、B、C、D、E、F 共 6 个字母。而用 3 位二进制数表示(编码)一个字母,则足可以表示 8 个字母(从二进制的 000 到二进制的 111),所以用 3 位二进制数(字符)表达这段文字内容涉及的 6 个字母绰绰有余
如下图所示,注意,这属于固定长度编码:
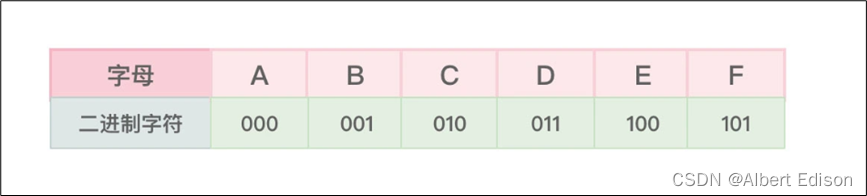
在传输文字内容 “AFDBCFBDEFDF” 时,传输的数据就是编码后 000101011001010101001011100101011101。
接收方可以按照双方事先的约定,也就是 3 位一划分来将二进制编码译码还原为真正的文字内容。但是如果传输的文字内容特别多,那么编码后的内容也将非常的长,这意味着传输的内容也会非常多。
事实上,在真正的数据传输中,不管传输的是英文字母、汉字等等,字母或者汉字出现的频率并不相同,比如在英文的 26 个字母中 “E、A、T、I、N、O” 出现的频率就会明显高于其他字母,而在汉字中 “有、人、的、工、在、一、是” 等出现的频率也会比其他汉字更高。
3. 哈夫曼编码
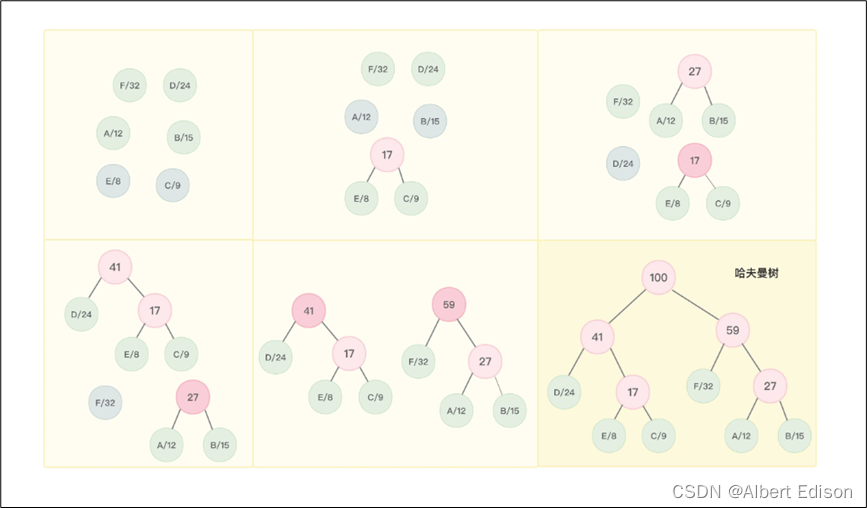
针对前面传输的文字内容 “AFDBCFBDEFDF” 中所包含的 6 个字母,可以粗略估算也可以假设它们出现的频率,按照出现频率一共 100% 计算,大略估计这 6 个字母的出现频率为 A:12%、B:15%、C:9%、D:24%、E:8%、F:32%。
有了这种估计,就可以按照哈夫曼树来重新进行编码规划 —— 将 A、B、C、D、E、F 这 6 个字母分别看做叶子节点,将这 6 个字母的百分比(去掉百分号)12、15、9、24、8、32 分别看做叶子节点的权值,这样就可以构造出一棵哈夫曼树。
如下图所示:
针对上图所展示的哈夫曼树,如果左分支路径中的各个段用 0 标示,右分支路径的各个段用 1 标示,换句话说,从根节点出发,向左走表示二进制的 0,向右走表示二进制 1,那么这种用二进制字符表示字母的方案就可以映射为树的表示形式。如下图所示:
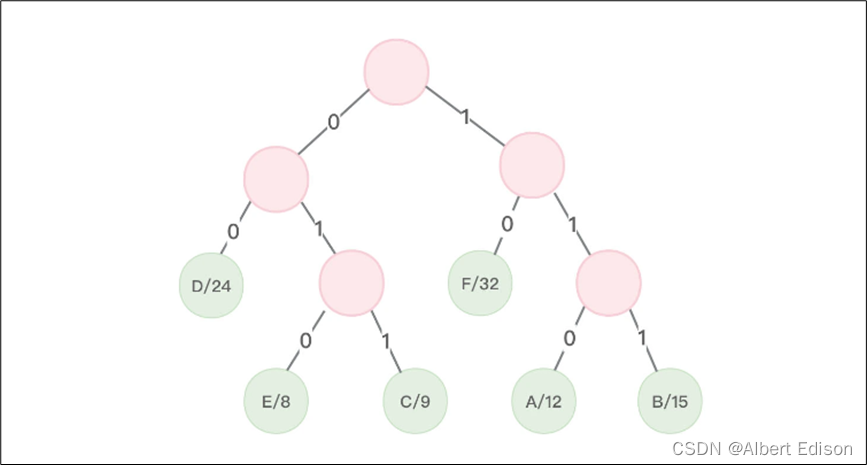
从上图可以看到,从根节点出发,访问节点 D 需要经过的路径所包含的二进制数为 00,节点 E 经过的路径所包含的二进制数为 010……,这意味着 D 的编码是 00,E 的编码是 010……。
那么哈夫曼树的 叶子节点 所对应的二进制编码如下图所示(这些字母对应的二进制字符编码就是 哈夫曼编码)。

从上图中可以看到,出现频率最高的字母,尽可能用最短的编码以节省数据通信量,所以这是一种可变长度编码,也就是不同的字母编码后对应的二进制字符长度不同。
最终,要传输的文字内容是 “AFDBCFBDEFDF”,而实际传输的内容是编码后的 11010001110111011100010100010。
可以与原来需要传输的二进制字符对比一下:
- 原二进制字符串:
000101011001010101001011100101011101(36 个字符) - 新二进制字符串:
11010001110111011100010100010(29 个字符)
这意味着需要传输的数据变少了,也就是数据被压缩了。节省了大概 19% 的保存或传输成本。显然,如果要传输的文字内容更多,所节省的成本也将更加可观。
4. 哈夫曼解码
那么如何从新的二进制字符串中把真正的文字内容解码出来呢?因为编码中只有 0 和 1,而且是一种可变长度的编码,在解码时其实是容易因混淆而导致解码错误的,所以,对于可变长度的编码,设计时必须保证任何一个字母的编码都不可以是另一个字母编码的前缀。
比如字母 F 的二进制编码是 10,那么其他字母在编码时绝对不可以以 10 开头,观察上=下图,字母 A、B、C、D、E 的二进制字符都不是以 10 开头。

这里涉及一个概念:前缀编码
- 如果在一个编码方案中,任何一个编码都不是其他任何编码的前缀(最左子串),则称该编码是前缀编码。
哈夫曼编码就属于一种前缀编码。
举个例子,假设字母 C 的二进制编码不是 011 而是 101,因为以 10 开头了是不被允许的,那么如果传输的内容是 10110110,接收方在解码时可能会解码为 CCF,也可能会解码为 FAA,这样就产生了歧义和混乱。
而按照上图这样编码,在收到新二进制字符串时,解码出来的内容只能是 “AFDBCFBDEFDF”,绝不会解码成其他内容。当然,为了保证发送方发送的内容接收方能够成功解码,接收方手中也必须有一份上图所示的编码表。
5. 编码特点
哈夫曼编码是用构造哈夫曼树的方法来确定字符集的一种编码方案,属于一种前缀编码,在解码时可以保证解出的内容的唯一性。
- 字符集中的每一个字符作为叶子节点,将各个字符出现的频率作为该节点的权值,构造出哈夫曼树。
- 将哈夫曼树左分支路径中的各个段用 0 标示,右分支路径中的各个段用 1 标示。当然,左分支用 1 标示,右分支用 0 标示也可以,只要通信双方在编码和解码时做好一致的约定就可以。
- 从哈夫曼树的根节点到叶子节点所经过的各段路径所对应的 0 或者 1 连接起来就构成了字符的哈夫曼编码。
因为哈夫曼树具有不唯一性,因此哈夫曼编码也是不唯一的。构建哈夫曼树时,有些资料上会建议左孩子节点的权值应该不大于右孩子节点的权值,或者要求左孩子与右孩子节点权值大小关系应该保持一致。
换句话说,就是要么保证所有左孩子节点权值小于或等于右孩子节点权值,要么保证所有右孩子节点权值小于或者等于左孩子节点权值(不需要保持左右孩子节点权值大小关系的一致性)。
6. 代码实现
哈夫曼编码的实现代码可以直接放在上篇文章中的 HFMTree 类中实现,增加 public 修饰的成员函数即可。
//生成哈夫曼编码
bool CreateHFMCode(int idx) //参数idx是用于保存哈夫曼树的数组某个节点的下标
{
//调用这个函数时,m_length应该已经等于整个哈夫曼树的节点数量,那么哈夫曼树的叶子节点数量应该这样求
int leafNodeCount = (m_length + 1) / 2;
if (idx < 0 || idx >= leafNodeCount)
{
//只允许对叶子节点求其哈夫曼编码
return false;
}
string result = ""; //保存最终生成的哈夫曼编码
int curridx = idx;
int tmpparent = m_data[curridx].parent;
while (tmpparent != -1) //沿着叶子向上回溯
{
if (m_data[tmpparent].lchild == curridx)
{
//前插0
result = "0" + result;
}
else
{
//前插1
result = "1" + result;
}
curridx = tmpparent;
tmpparent = m_data[curridx].parent;
} //end while
cout << "下标为【" << idx << "】,权值为" << m_data[idx].weight << "的节点的哈夫曼编码是" << result << endl;
return true;
}
在主函数中增加测试样例
//哈夫曼编码测试
int main()
{
int weigh[] = { 12,15,9,24,8,32 };
int sz = sizeof(weigh) / sizeof(weigh[0]);
//分别传入:权值列表中元素个数 和 权值列表首地址
HFMTree hfmt(sz, weigh);
hfmt.CreateHFMTree(); //创建哈夫曼树
hfmt.preOrder(hfmt.GetLength() - 1); //遍历哈夫曼树,参数其实就是根节点的下标(数组最后一个有效位置的下标)
//求哈夫曼编码
cout << "--------------" << endl;
for (int i = 0; i < sz; ++i)
hfmt.CreateHFMCode(i);
return 0;
}
测试结果如下:
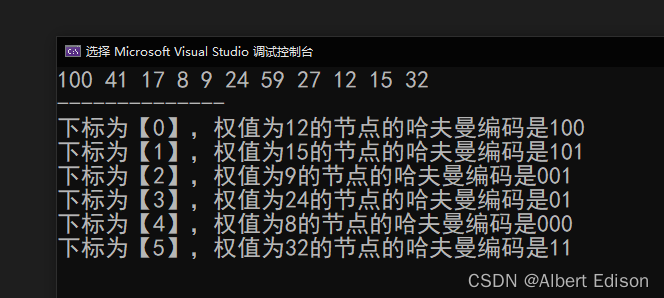
请注意,该结果与上图所展示的哈夫曼编码结果不完全一样,这是因为程序编码中哈夫曼树的构建规则完全遵照 “哈夫曼树左孩子节点的权值不大于右孩子节点的权值”,而上面图中的哈夫曼树并没有遵照这个规则构建(例如节点 24 和 17 结合的时候,还有节点 32 和 27 结合的时候)。
7. 总结
哈夫曼树是用来创建哈夫曼编码的。哈夫曼编码是一种可以用于数据压缩的编码方式,哈夫曼编码的构造过程需要用到哈夫曼树。
思考:英文的 26 个字母使用的频率是不一样的,这 26 个字母的使用频率数据可以通过搜索引擎来搜索。如果要对这 26 个字母进行哈夫曼编码,计算一下使用哈夫曼编码可以对数据压缩多少?