序列（Sequence）是有顺序的数据列，Python 有三种基本序列类型：list, tuple 和 range 对象，序列（Sequence）是有顺序的数据列，二进制数据（bytes） 和 文本字符串（str）也是序列类型，它们是特殊序列类型，会有一些特殊的性质和操作。

在实际的使用中，我们并不直接使用序列（Sequence）类型，而是具体使用list、tuple和range对象等等，本文主要是做一个归纳、概括性的说明

序列类型

Python 的内置序列类型有：

类型	创建方法	可变性	特别方法
列表	list()	可变	sort()
元组	tuple()	不可变
等差数列	range()	不可变	属性方法
字符串	str()	不可变	字符的方法
字节串	bytes()	不可变
字节数组	bytearray()	可变
内存视图	memoryview()	不可变

要注意的是，集合、字典不是序列类型，虽然字典在最新的 Python 版本中具备了元素顺序特性，但这不是一种「保证」。

可以通过 

isinstance(obj, collections.Sequence)

来判定对象是不是一个序列类型。

扁平序列

扁平序列有两个特点，第一，内部存储的都是值而不是引用（或者说是内存地址）；第二，内部存储的都是同一种数据类型，而且只能存储数值、字节、字符这样的基础数据类型。常见的扁平序列如字符串str、字节bytes、数组array.array、字节数组bytearray和内存视图memoryview等。

我们举一个例子，例如s1 = 'abc'，这是一个创建字符序列str的命令。这条命令运行时，Python解释器会先在内存中开辟一块连续的内存空间来存储a、b和c三个字符，创建好对象后会将这块内存的首地址抛给外界，由变量s1来接收，变量s1是另一块内存，这块内存中就存储了字符串序列'abc'的内存首地址。之后如果需要使用'abc'这个对象，都是通过变量s1。当解释器读到变量s1时，发现其存储的是一个内存地址，就会直接读取这个内存地址对应数据，完成对象的访问。

 

 

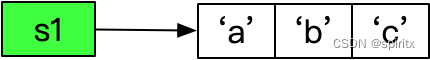
容器序列

与扁平序列相对应，容器序列中存储的不是值而是对象的引用，正因为如此，容器中可以容纳任何数据类型。常见的容器序列包括列表list、元祖tuple等。

如下例子：list1 = [1,'abc',[10,20,’age']]，这是一个列表。

 

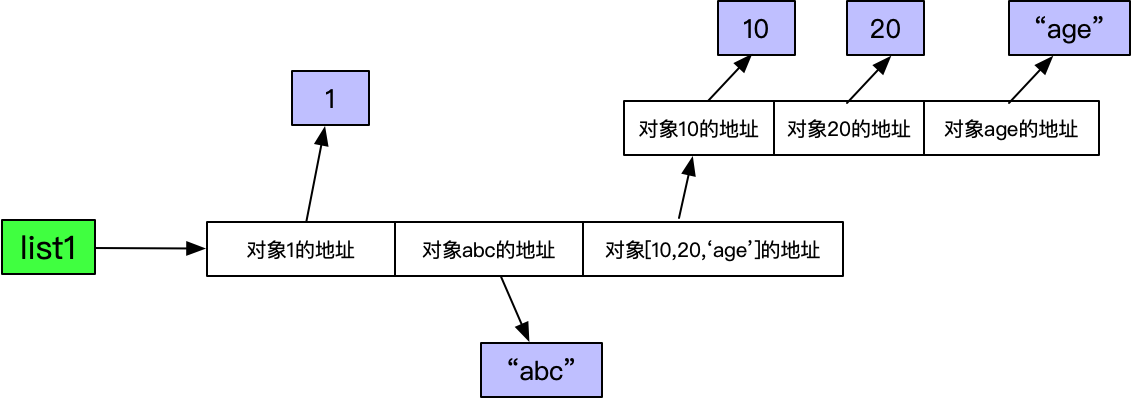
可以看到，对于列表本身来说，其在内存中是连续的，但是列表的内存中存储的并不是值本身，而是对象（列表中元素）的引用。至于对象（列表中的元素）本身，则存储在别的内存块中，这些内存可能是连续的，也可能是不连续的，大概率是不连续的。而且，列表中不仅仅可以存储基本数据类型int、str，还可以存储列表list。

可变序列

可变序列是指可以在原内存地址上对数据进行修改的序列。这类序列包括列表list、字节数组bytearray、数组array.array，内存视图memoryview等。

列表list提供了append方法，可以在原列表内存地址上对列表进行修改：

>>> b = [1,2,3]
>>> id(b)
4352472384
>>> b.append(4)
>>> id(b)   #追加了元素，但是b的地址并没有变化
4352472384
>>> b
[1, 2, 3, 4]

这里给列表增加了一个元素，但是列表的内存地址并没有发生变化。

不可变序列

不可变序列指的是不可以在原内存地址上对序列进行修改。这类序列包括字符序列str、元祖tuple、和字节序列bytes。

例如，对于字符序列str，一旦创建就无法在原内存地址上对数据进行修改，强行修改则是创建新的对象：

>>> s = 'abc'
>>> id(s)
4346120656
>>> s = '123'
>>> id(s)   #s的内容和地址都变化了
4349997680
>>> s
'123'
>>> s += '4'
>>> id(s)  #即使是追加，s的内容和地址也都变化了
4349376816
>>> s
'1234'

可能有人对元祖不可修改无法理解，对于容器序列来说，不可变指的是容器中每一个元素的引用不可变，而不是每一个元素的值不可变。如下面的例子：

>>> a = ('1','2',['3','4'])
# 记录元祖的内存地址
>>> id(a)
1665412226688
# 记录元祖中第一个元素的内存地址
>>> id(a[0])
140710344787616
# 修改元祖中的第一个元素，可以看到报错了，提示元祖对象不支持赋值。因为第一个元素是一个不可变对象，强行修改会创建新的对象，产生新的引用，而元祖不支持修改内部元素的引用，所以报错。
>>> a[0]='5'
Traceback (most recent call last):
  File "<pyshell#14>", line 1, in <module>
    a[0]='5'
TypeError: 'tuple' object does not support item assignment
# 记录元祖中第三个元素列表的内存地址
>>> id(a[2])
1665412212544
# 我们的元祖中第三个元素是一个list，这是一个可变的序列，使用append方法会在原内存地址上进行修改，这样保证元素中第三个元素的引用并不会发生变化，所以修改成功。
>>> a[2].append('9')
# 可以看到第三个元素列表修改成功
>>> a
(1, 2, [3, 4, 9])
# 但是第三个元素的内存地址并未发生变化
>>> id(a[2])
1665412212544
# 元祖第三个元素修改后，元祖本身的内存地址并未发生变化。
>>> id(a)
1665412226688

这个例子中，我们先创建了一个元祖(1,2,[3,4])，元祖中有三个元素1、2、[3,4]，前两个都是不可变的字符序列str，通过前面的例子我们已经知道，如果对字符序列强行修改，不会改变原来的字符，而是创建新的对象。新的对象就意味着产生一个新的内存地址，这会导致元祖第一个元素的引用发生变化。这是元祖不能够接受的，所以出现报错。

然而，我们发现对创建的元祖的第三个元素进行修改，却修改成功了，原因是第三个元素是一个列表list，是一个可变序列，对其调用append方法是在原地址上对数据进行的修改，而并不会改变本身的内存地址，因此元祖第三个元素的引用不会发生变化，故而修改成功。

因此我们说对于容器序列，不可变意味着元素的引用不可变，相反，可变则意味着引用可以发生变化：

>>> a = [1,2,[3,4]]
>>> id(a)
2338191916032
>>> id(a[2])
2338200822784
>>> a[2]=5
>>> a
[1, 2, 5]
>>> id(a[2])
140710407702304
>>> id(a)
2338191916032

 看见列表是可以修改元素的引用的，因为它是可变类型。

序列类型的协议

以上我们对Python中的序列类型进行了分类，接下来我们学习一下序列类型的协议。通过这一部分的学习，你会对面向对象以及常见序列类型有更加深刻的认识。

Python为可变序列和不可变序列提供了两个基类Sequence和MutableSequence，这两个基类存在于内置模块collections.abc中，与其他常见的类如int、list等不同，这两个基类都是抽象基类，抽象基类确定了序列类型的协议，所有属于序列类型的都要遵循这个抽象基类的协议。

Sequence和MutableSequence两个类的继承关系如下：

 

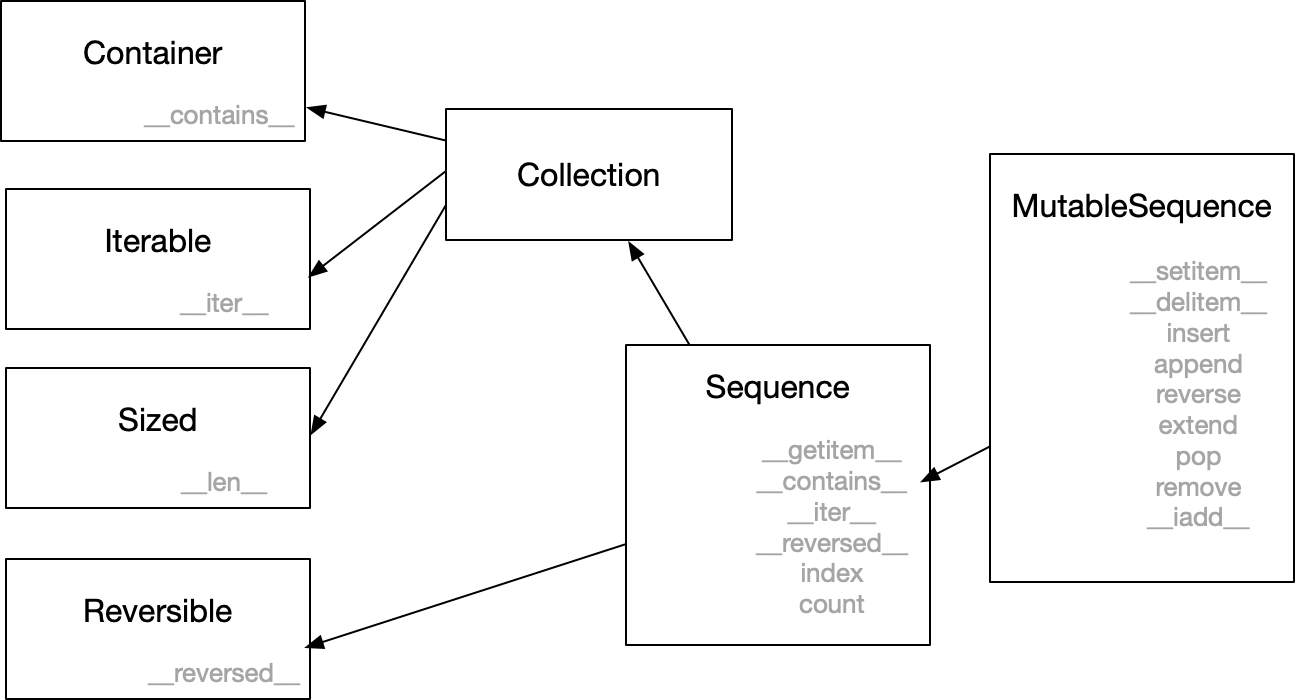
可变序列MutableSequence类继承自不可变序列Sequence类，Sequence类又继承了两个类Reversible和Collection，Collection又继承自Container、Iterable、Sized三个抽象基类。通过这个继承图，我们至少应该能够知道，对于标准不可变序列类型Sequence，应该至少实现以下几种方法（遵循这些协议）：

__contains__,__iter__，__len__，__reversed__，__getitem__，index，count

 以Python的内置类型list为例说明这几个方法：

• 实现了__contains__方法，就意味着list可以进行成员运算，即使用in和not in；
• 实现了__iter__方法，意味着list是一个可迭代对象，可以进行for循环、拆包、生成器表达式等多种运算；
• 实现了__len__方法，意味着可以使用内置函数len()。同时，当判断一个list的布尔值时，如果list没有实现__bool__方法，也会尝试调用__len__方法；
• 实现了__reversed__方法，意味着可以实现反转操作；
• 实现了__getitem__方法，意味着可以进行索引和切片操作；
• 实现了index和count方法，则表示可以按条件取索引和统计频数。

标准的Sequence类型声明了上述方法，这意味着继承自Sequence的子类，其实例化产生的对象将是一个可迭代对象、可以使用for循环、拆包、生成器表达式、in、not in、索引、切片、翻转等等很多操作。这同时也表明，如果我们说一个对象是不可变序列时，暗示这个对象是一个可迭代对象、可以使用for循环、......。

而对于标准可变序列MutableSequence，我们发现，除了要实现不可变序列中几种方法之外，至少还需要实现如下几个方法（遵循这些协议）：

__setitem__,__delitem__,insert,append,extend,pop,remove,__iadd__

以Python的内置类型list为例这几个方法：

• 实现了__setitem__方法，就可以对列表中的元素进行修改，如代码a[0]=2就是在调用这个方法
• 实现了__delitem__,pop,remove方法，就可以对列表中的元素进行删除，如代码del a[0]就是在调用__delitem__方法
• 实现了insert,append,extend方法，就可以在序列中插入元素；
• 实现了__iadd__方法，列表就可以进行增量赋值。

这就是说，对于标准可变序列类型，除了执行不可变类型的查询操作之外，其子类的实例对象都可以执行增删改的操作。

鸭子类型

抽象基类Sequence和MutableSequence声明了对于一个序列类型应该实现那些方法，很显然，如果一个类直接继承自Sequence类，内部也重载了Sequence中的七个方法，那么显然这个类一定是序列类型了，MutableSequence的子类也是一样。确实如此，但是当我们查看列表list、字符序列str、元组tuple的继承链时，发现在其mro列表（Method Resolution Order, MRO代表了类继承的顺序）中并没有Sequence和MutableSequence类，也就是说，这些内置类型并没有直接继承自这两个抽象基类。

>>> list.__mro__
(<class 'list'>, <class 'object'>)
>>> tuple.__mro__
(<class 'tuple'>, <class 'object'>)
>>> str.__mro__
(<class 'str'>, <class 'object'>)

其实，Python中有一种被称为“鸭子类型”的编程风格。在这种风格下，我们并不太关注一个对象的类型是什么，它继承自那个类型，而是关注他能实现那些功能，定义了那些方法。正所谓如果一个东西看起来像鸭子，走起来像鸭子，叫起来像鸭子，那他就是鸭子。

在这种思想之下，如果一个类并不是直接继承自Sequence，但是内部却实现了__contains__,__iter__，__len__，__reversed__，__getitem__，index，count几个方法，我们就可以称之为不可变序列。甚至都不必这么严格，可能只需要实现__len__，__getitem__两个方法就可以称作是不可变序列类型。对于可变序列也同样如此。

序列的操作

序列的特点是由若干元素组成，元素的分布有顺序，因此根据这个特点，它们支持一些共性的操作。

通用操作

以下是所有序列类型均支持的操作：

运算	结果	备注
x in s	如果 s 中的某项等于 x 则结果为 True，否则为 False
x not in s	如果 s 中的某项等于 x 则结果为 False，否则为 True
s + t	s 与 t 相拼接
s * n 或 n * s	相当于 s 与自身进行 n 次拼接
s[i]	s 的第 i 项，起始为 0	切片操作
s[i:j]	s 从 i 到 j 的切片
s[i:j:k]	s 从 i 到 j 步长为 k 的切片
len(s)	s 的长度
min(s)	s 的最小项
max(s)	s 的最大项
s.index(x[, i[, j]])	x 在 s 中首次出现项的索引号 （索引号在 i 或其后且在 j 之前）	count 方法
s.count(x)	x 在 s 中出现的总次数	index 方法
for i in x:pass	迭代
hash(x)	对象的哈希值	仅不可变序列
sorted(x)	排序
all(x) 或者 any(x)	全真或者有真检测
iter(x)	生成迭代器

可变序列类型

以下是仅可变序列支持的操作：

运算	结果：
s[i] = x	将 s 的第 i 项替换为 x
s[i:j] = t	将 s 从 i 到 j 的切片替换为可迭代对象 t 的内容
del s[i:j]	等同于 s[i:j] = []
s[i:j:k] = t	将 s[i:j:k] 的元素替换为 t 的元素
del s[i:j:k]	从列表中移除 s[i:j:k] 的元素
s.append(x)	将 x 添加到序列的末尾 (等同于 s[len(s):len(s)] = [x])
s.clear()	从 s 中移除所有项 (等同于 del s[:])
s.copy()	创建 s 的浅拷贝 (等同于 s[:])
s.extend(t) 或 s += t	用 t 的内容扩展 s (基本上等同于 s[len(s):len(s)] = t)
s *= n	使用 s 的内容重复 n 次来对其进行更新
s.insert(i, x)	在由 i 给出的索引位置将 x 插入 s (等同于 s[i:i] = [x])
s.pop() 或 s.pop(i)	提取在 i 位置上的项，并将其从 s 中移除
s.remove(x)	删除 s 中第一个 s[i] 等于 x 的项目。
s.reverse()	就地将列表中的元素逆序。