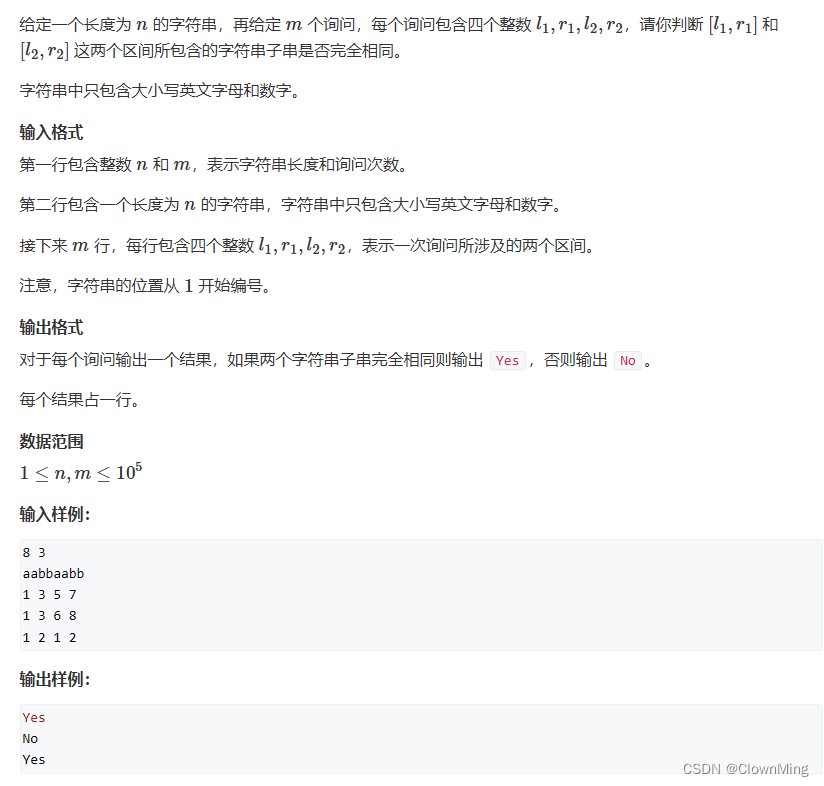
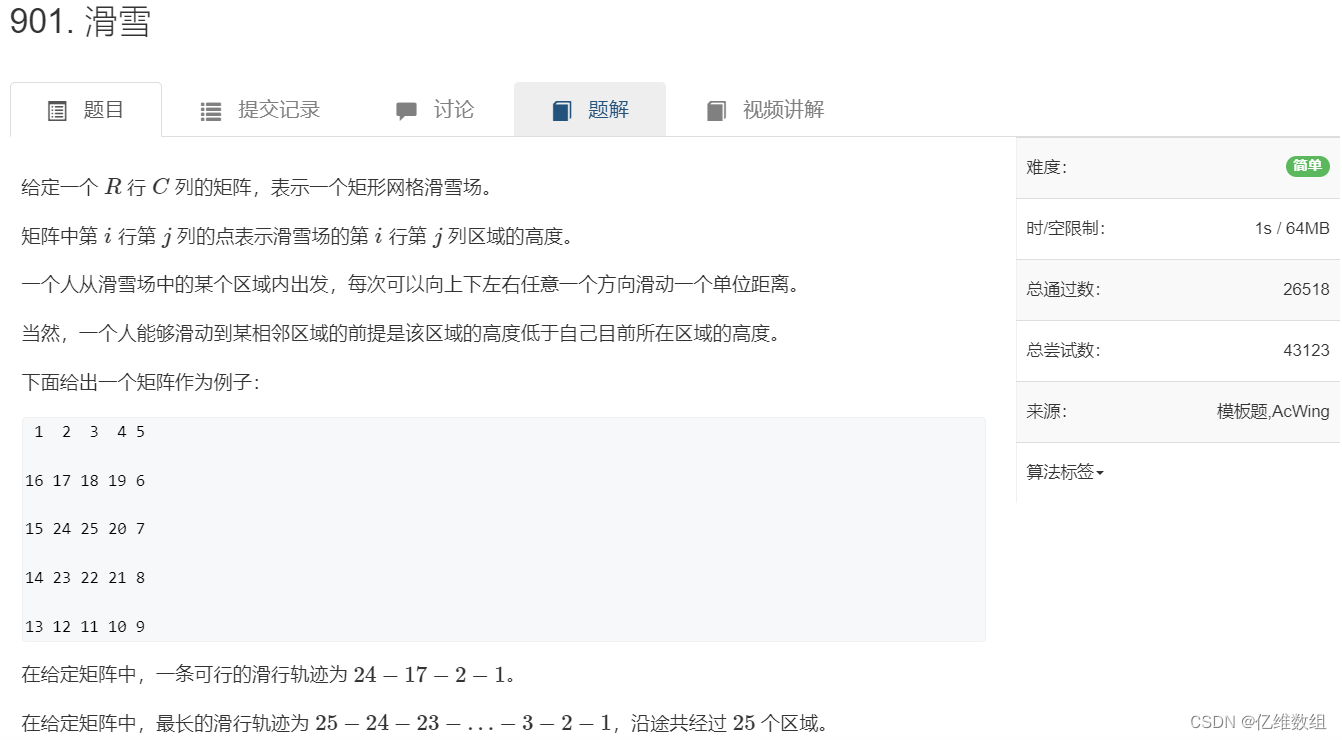
题目描述

 题目分析

样例解释

轨迹如下所示

状态表示

可以用f[i,j]表示从点（i，j）开始往下滑的最长的滑雪轨迹，那么最终答案就是遍历每一个点的f[i,j]，然后取最大值

状态计算

状态的转移也是非常的简单，对于一个坐标(i,j)，去看这个坐标的上下左右的点(x,y)的高度是否比这个点要低，如果确实低，那么就取f[i,j]和f[x,y]+1的最大值，即状态转移方程为：

此处在遍历一个点（i,j）的上下左右点的时候可以使用非常经典的方向数组dx，dy（迷宫等bfs问题中的常客），详细看代码

时间复杂度与记忆化思想

为了体现出“记忆化”，可以先把f[x,y]的所有值初始化为-1，如果某一个点比如(i,j）已经处理完了，比如说f[i,j]已经算出了是a，那么这个对应的以（i，j）为起点的轨迹的每一个点的f数组都已经得到结果，值也不再是-1，当下次算某一个点比如（k，c）的轨迹时，如果遍历到某一个点之前算过且f数组不再是-1，那么就可以直接拿来去用。总之，可以发现，通过这种方法，实际上每一个点仅仅需要遍历一次，所以总共的时间复杂度就是O（nm）

代码

#include<cstring>
#include<iostream>
using namespace std;
const int N=310;
int n,m;
int h[N][N];
int f[N][N];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int dp(int x,int y)
{
    int &r=f[x][y];
    if(r!=-1)return r;
    r=1;
    for(int i=0;i<4;i++)
    {
        int tx=x+dx[i],ty=y+dy[i];
        if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&h[tx][ty]<h[x][y])
        r=max(r,dp(tx,ty)+1);
    }
    return r;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        cin>>h[i][j];
    }
    memset(f,-1,sizeof f);
    int res=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            res=max(res,dp(i,j));
    cout<<res<<endl;
    return 0;
}