数值类特征

数值类特征是最常见的一种特征类型，数值可以直接喂给算法。
为了提升效果，我们需要对数值特征做一些处理，本文介绍了4种常见的处理方式：缺失值处理、二值化、分桶、缩放。

什么是数值类特征？

数值类特征就是可以被实际测量的特征。例如：

• 人的身高、体重、三维
• 商品的访问次数、加入购物车次数、最终销量
• 登录用户中有多少新增用户、回访用户

数值类的特征可以直接喂给算法，为什么还要处理？

因为好的数值特征不仅能表示出数据隐藏的中的信息，而且还与模型的假设一致。通过合适的数值变换就可以带来很好的效果提升。

例如线性回归、逻辑回归对于数值的大小很敏感，所以需要进行缩放。

对于数值类特征，我们主要关注2个点：

1. 大小
2. 分布

下面提到的4种处理方式都是围绕大小和分布来优化的。

数值类特征常用的4种处理方式

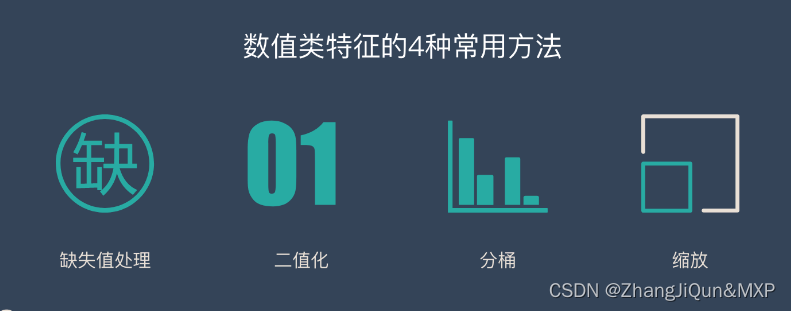
1. 缺失值处理
2. 二值化
3. 分桶 / 分箱
4. 缩放

缺失值处理：处理缺失值

在实际问题中，经常会遇到数据缺失的情况。缺失值对效果会产生较大的影响。所以需要根据实际情况来处理。

对于缺失值常用3种处理方式：

1. 填充缺失值（均值、中位数、模型预测…）
2. 删除带有缺失值的行
3. 直接忽略，将缺失值作为特征的一部分喂给模型进行学习

二值化：处理差距过大数据

这种处理方式通常用在计数的场景，例如：访问量、歌曲的收听次数…

举例：

根据用户的听音乐的数据来预测哪些歌曲更受欢迎。

假设大部分人听歌都很平均，会不停的听新的歌曲，但是有一个用户24小时的不停播放同一首歌曲，并且这个歌曲很偏门，导致这首歌的总收听次数特别高。如果用总收听次数来喂给模型，就会误导模型。这时候就需要使用「二值化」。

同一个用户，把同一首歌听了N遍，只计数1，这样就能找出大家都喜欢的歌曲来推荐。

分桶 / 分箱：处理差距过大数据

拿每个人的收入举例，大部分人的收入都不高，极少数人的收入极其高，分布很不均匀。有些人月收入3000，有些人月收入30万，跨了好几个数量级。

这种特征对于模型很不友好。这种情况就可以使用分桶来处理。分桶就是将数值特征分成不同的区间，将每个区间看做一个整体。

常见的分桶：

1. 年龄分布
2. 商品价格分布
3. 收入分布

常用的分桶方式：

1. 固定数值的分桶（例如年龄分布：0-12岁、13-17岁、18-24岁…）、
2. 分位数分桶（例如淘宝推荐的价格区间：30%用户选择最便宜的价格区间、60%用户选择的中等价格区间、9%的用户选择最贵的价格区间）
3. 使用模型找到最佳分桶

 

缩放：归一化

线性回归、逻辑回归对于数值的大小很敏感、不同特征尺度相差很大的话会严重影响效果。

所以需要将不同量级的数值进行归一化。将不同的数量级缩放到同一个静态范围中（例如：0~1，-1~1）。

常用的归一化方式：

1. z分数标准化
2. min-max标准化
3. 行归一化
4. 方差缩放