目录
题目
题目初步解析
水桶效应
代码实现逻辑
第一步
第二步
第三步
代码具体实现
注意
添加容器元素的函数
计算迭代并且判断面积是否是最大值
总代码
运行结果
总结
题目
给定一个长度为
n的整数数组height。有n条垂线,第i条线的两个端点是(i, 0)和(i, height[i])。找出其中的两条线,使得它们与
x轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明:你不能倾斜容器。
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
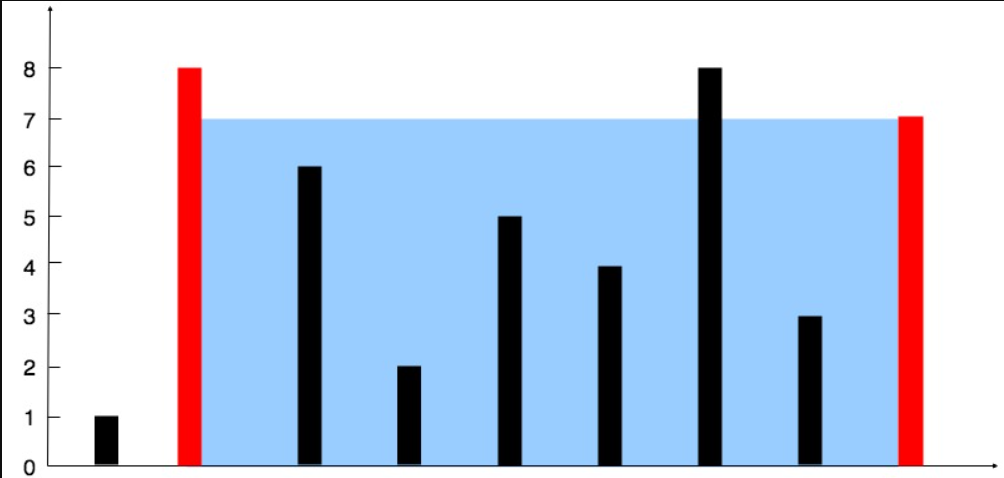
题目初步解析
这一道题就是我们小时候常常说的水桶效应
水桶效应
水桶效应是指一只水桶想盛满水,必须每块木板都一样平齐且无破损,如果这只桶的木板中有一块不齐或者某块木板下面有破洞,这只桶就无法盛满水。是说一只水桶能盛多少水,并不取决于最长的那块木板,而是取决于最短的那块木板。也可称为短板效应。一个水桶无论有多高,它盛水的高度取决于其中最低的那块木板。
这就是我们要利用的思想来解答题目
代码实现逻辑
这是一个运用到双指针思想的问题(不一定用指针)
第一步
可以在数组的两侧(开头以及末尾)标记两个指针(或者记录下标)
然后计算面积
第二步
此时当然不能说这是最大的面积
我们要进行遍历
那怎么遍历呢?
还记得我们刚刚说的木头效应吗?
你装下的水取决于的是你最小的那一块木板
那如果要遍历的话
只能是短的一边进行更新,如果是左边的指针那就往右移动
如果是右边的就往左边进行移动
也就是都向“中间”更新
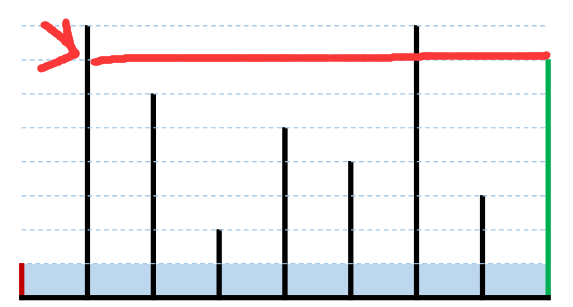
因为在横坐标两条垂线的距离降低的情况下,如果变化的是长边,盛水的长方形的高依旧不会变,不需要比较,那么面积必然会更小
第三步
那迭代出来的面积个数不止一个,怎么办呢?
分别比大小就可以了
第三步的步骤就是把每次迭代出来的值与之前的最大值比大小
如果更新的值更大,那就更新最大值就行
代码具体实现
注意
这里是展示所有代码可直接运行,但是力扣上的一个类,所以要改一下才可以跑
添加容器元素的函数
void addCounts(vector<int>& sum_1)
{
int length;
cout << "输入数组的长度" << endl;
cin >> length;
int i = 1;
while (i <= length)
{
int sum_2;
cout << "输入第" << i << "个元素" << endl;
cin >> sum_2;
sum_1.insert(sum_1.end(), sum_2);
i++;
};
}这里就是最基本的赋值就行
可以用链表的形式,当然我图方便用了容器
不过如果用链表的话那下面的函数要进行修改
这些方法都可以
计算迭代并且判断面积是否是最大值
int maxArea(vector<int> height)
{
int maxarea = 0;
int maxarea_1 = 0;
int i = 0;
int j = height.size() - 1;
//最左节点
int left_str = height[i];
//最右节点
int right_str = height[j];
while (i != j)
{
if (height[i] < height[j])
{
maxarea_1 = height[i] * (j - i);
if (maxarea < maxarea_1)
maxarea = maxarea_1;
i++;
}
else
{
maxarea_1 = height[j] * (j - i);
if (maxarea < maxarea_1)
maxarea = maxarea_1;
j--;
}
}
return maxarea;
}我这里是用下标进行定位的
计算面积同时判断大小
while语句中判断左边标记的下标等于右边的时候跳出循环
需要注意的是迭代的时候左边是++右边是--
总代码
总代码附上
#include <iostream>
#include <vector>
using namespace std;
//添加数组元素
void addCounts(vector<int>& sum_1)
{
int length;
cout << "输入数组的长度" << endl;
cin >> length;
int i = 1;
while (i <= length)
{
int sum_2;
cout << "输入第" << i << "个元素" << endl;
cin >> sum_2;
sum_1.insert(sum_1.end(), sum_2);
i++;
};
}
int maxArea(vector<int> height)
{
int maxarea = 0;
int maxarea_1 = 0;
int i = 0;
int j = height.size() - 1;
//最左节点
int left_str = height[i];
//最右节点
int right_str = height[j];
while (i != j)
{
if (height[i] < height[j])
{
maxarea_1 = height[i] * (j - i);
if (maxarea < maxarea_1)
maxarea = maxarea_1;
i++;
}
else
{
maxarea_1 = height[j] * (j - i);
if (maxarea < maxarea_1)
maxarea = maxarea_1;
j--;
}
}
return maxarea;
}
int main()
{
vector<int> sum_1;
addCounts(sum_1);
int maxarea = maxArea(sum_1);
cout << "*************************************************************************"<< endl;
cout <<"面积为" << maxarea << endl;
return 0;
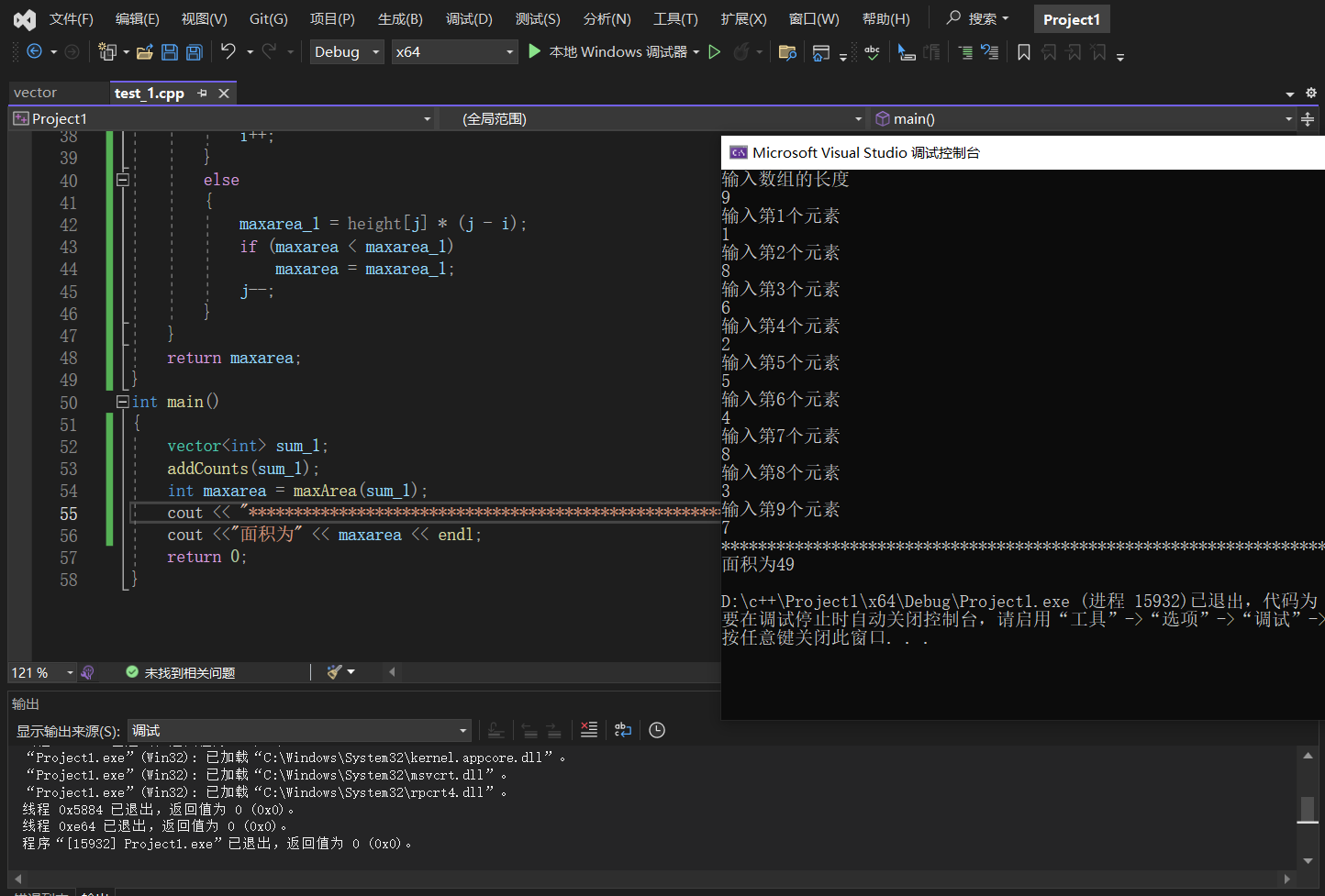
}运行结果
和题目得到示例得到的结果一样
总结
本次博客学习了一种新的思想,并且巧妙的运用了学到的木桶效应来进行解题