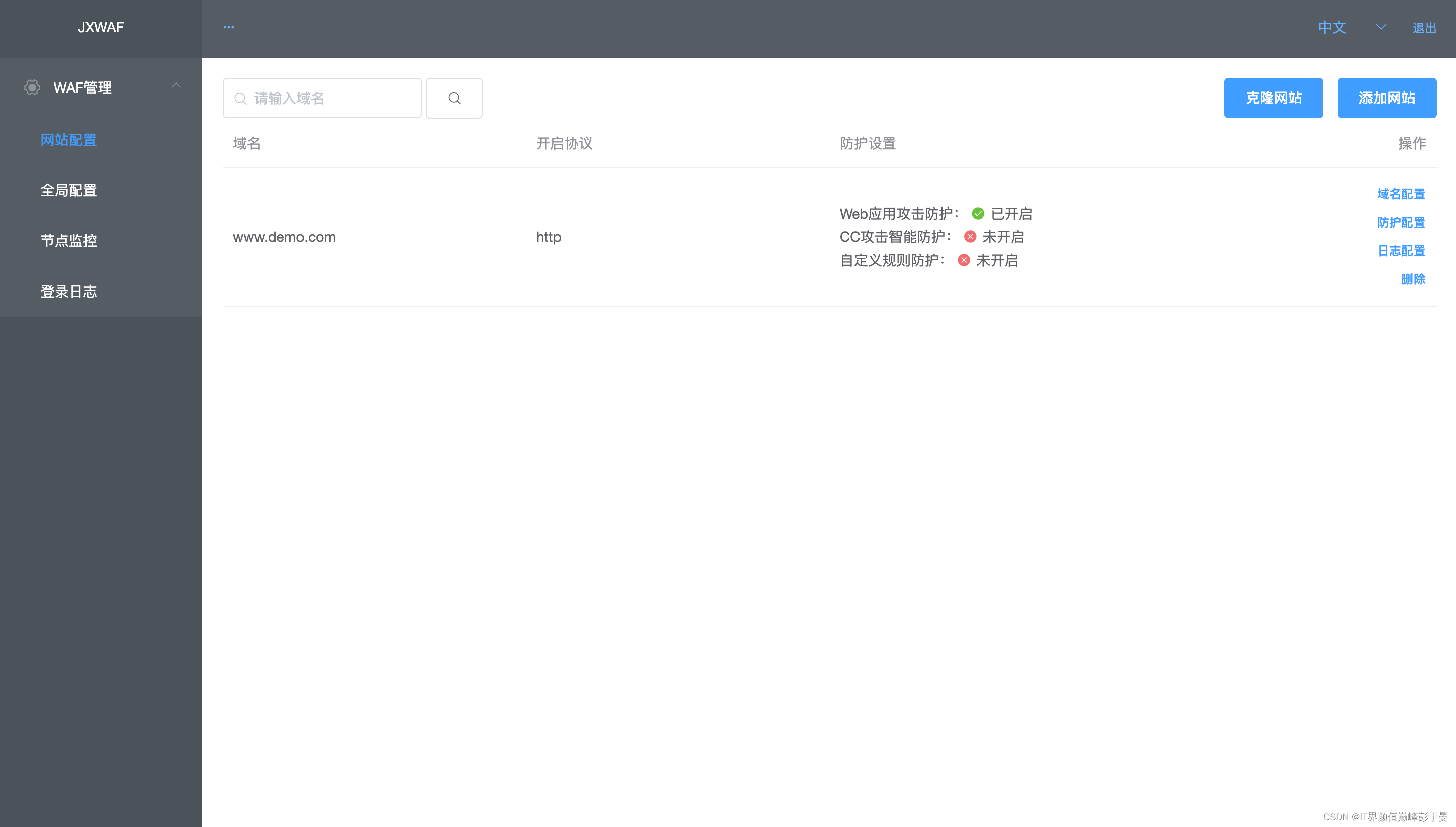
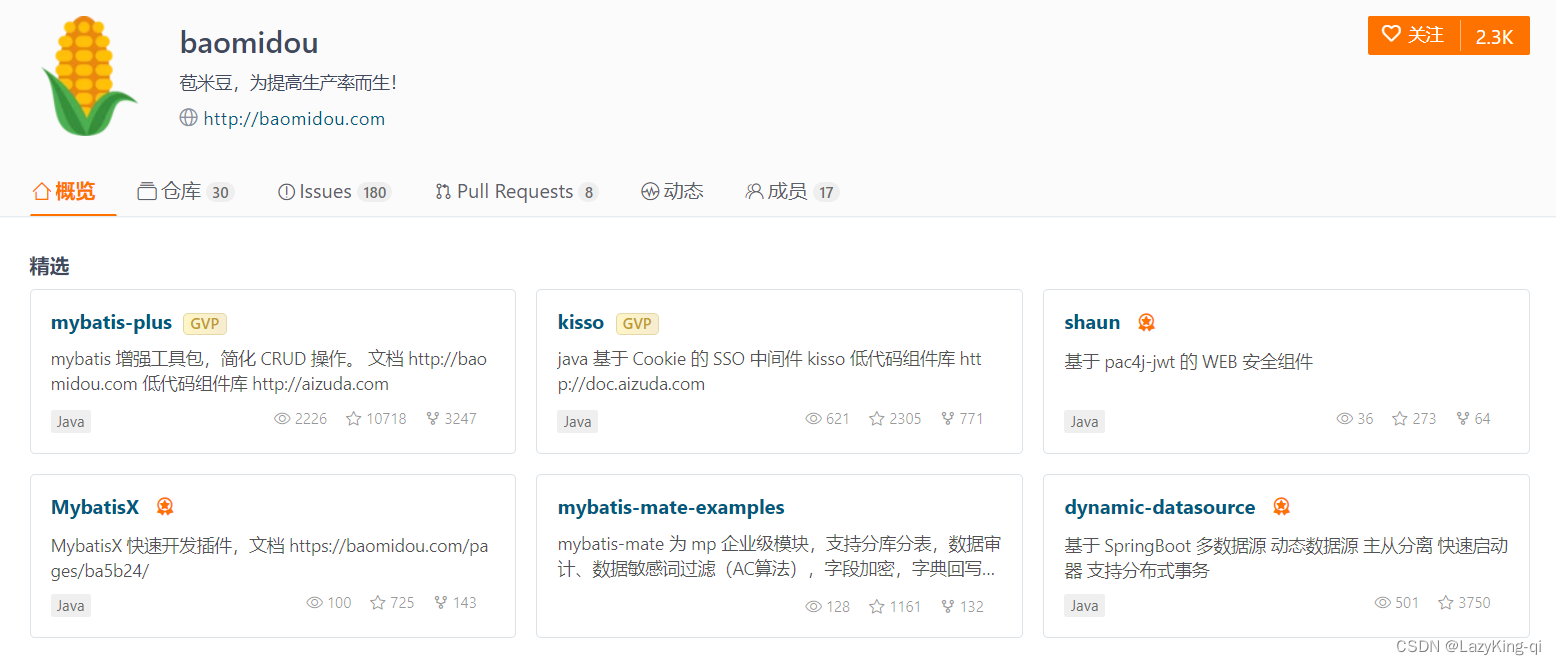
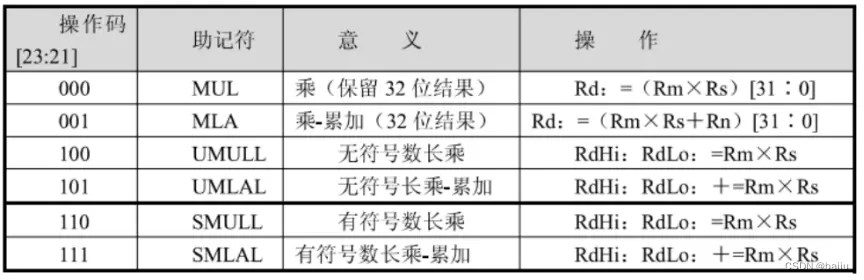
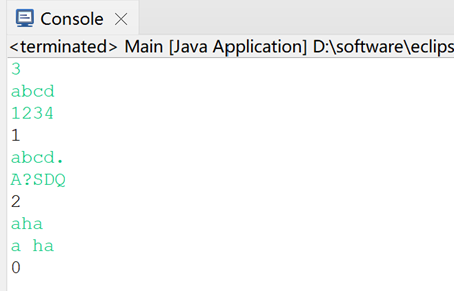
定义
f
(
x
)
−
f
(
a
)
x
−
a
{f(x) - f(a)\over x -a}
x−af(x)−f(a) 表示 f(x) 函数从 x 到 a 的平均变化率，如果使 x 趋近于 a，则表示函数在 a 点的变化率。
若有以下极限存在（定义域不包含a）：
lim
x
→
a
f
(
x
)
−
f
(
a
)
x
−
a
\lim \limits_{x\rightarrow a} {{f(x) - f(a)\over x - a}}
x→alimx−af(x)−f(a)
则称 f 于 a 处可导，并称这个极限为 f 于 a 处的导数，记作：
f
′
(
a
)
f^{'}(a)
f′(a)，也可记作 
，或者
d
(
f
)
d
(
x
)
(
a
)
{d(f)\over d(x)}(a)
d(x)d(f)(a)
几何意义
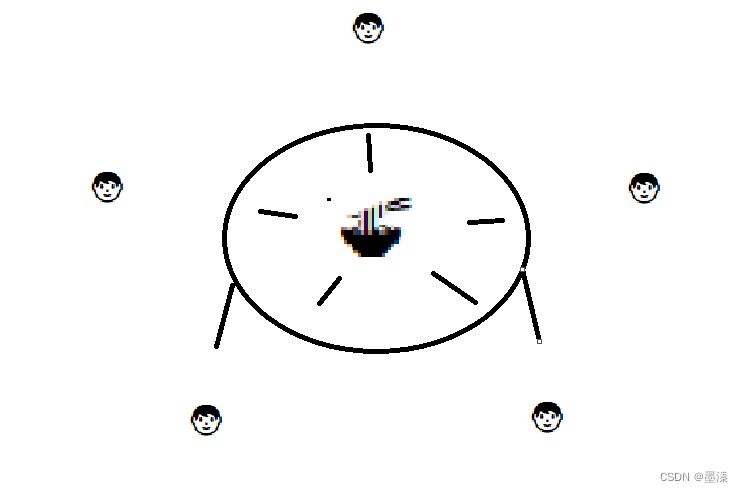
导数可以表示函数的曲线上的切线斜率，如下图：
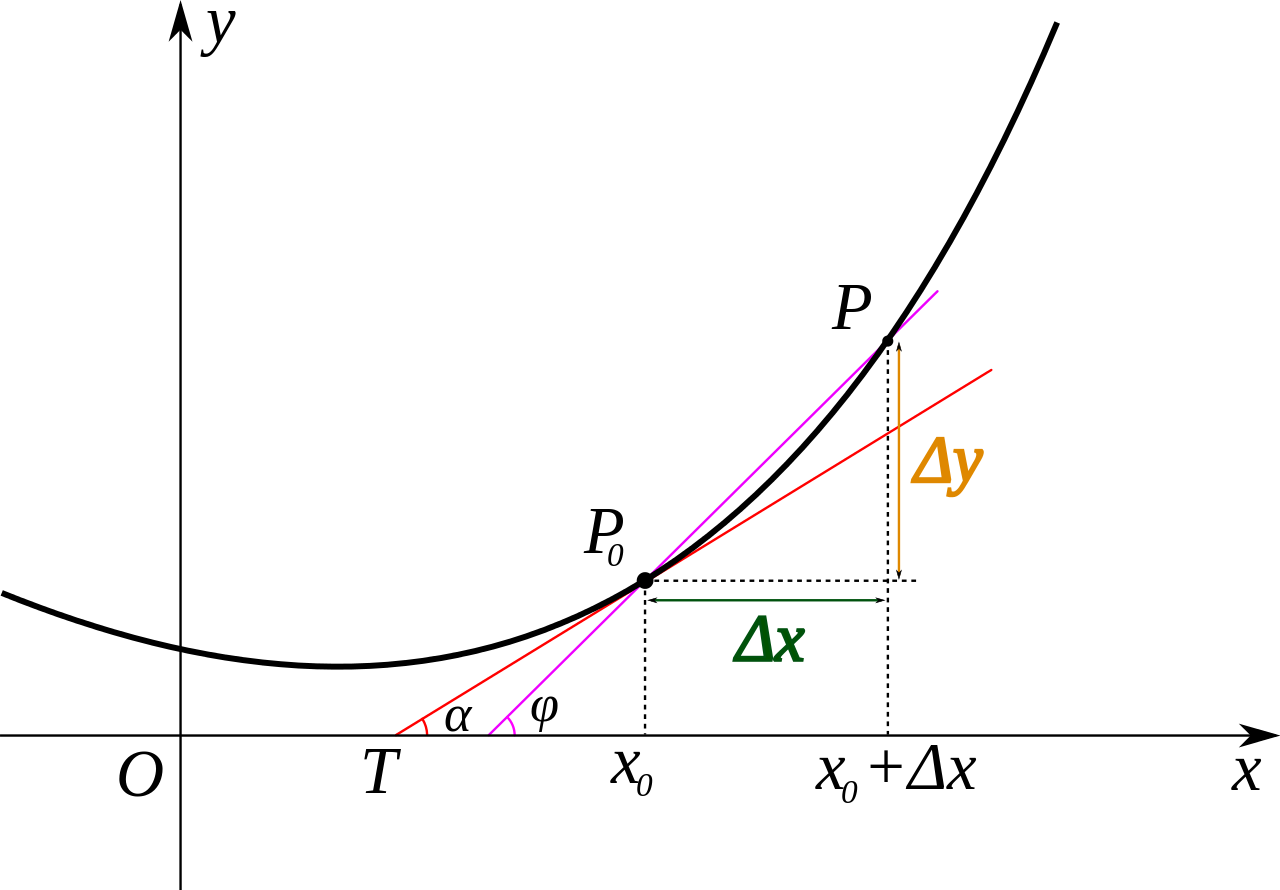
当
Δ
x
\Delta x
Δx 无穷小时，则 P 点趋近于 P0 点，割线 T 的斜率趋于 P0 点切线的斜率，记作：
t
a
n
α
=
Δ
y
Δ
x
=
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
tan\ \alpha = {\Delta y\over \Delta x} = {f(x0 + \Delta x) - f(x0) \over \Delta x}
tan α=ΔxΔy=Δxf(x0+Δx)−f(x0)
常用求导公式
- ( c ) ′ = 0 (c)^{'} = 0 (c)′=0
- ( x α ) ′ = α x ( α − 1 ) (x^{\alpha})^{'} = \alpha x^{(\alpha -1)} (xα)′=αx(α−1)
- s i n ( x ) ′ = c o s ( x ) sin(x)^{'} = cos(x) sin(x)′=cos(x)
- c o s ( x ) ′ = − s i n ( x ) cos(x)^{'} = -sin(x) cos(x)′=−sin(x)
- t a n ( x ) ′ = s e c 2 ( x ) tan(x)^{'} = sec^{2}(x) tan(x)′=sec2(x)
- ( a x ) ′ = a x l n a (a^{x})^{'} = a^{x} ln\ a (ax)′=axln a
- ( e x ) ′ = e x (e^{x})^{'} = e^{x} (ex)′=ex
- ( l o g a x ) ′ = 1 x l n a (log_ax)^{'} = {1\over x ln \ a} (logax)′=xln a1
- ( l n x ) ′ = 1 x (lnx)^{'} = {1\over x} (lnx)′=x1
基本求导法则
- ( u ± v ) = u ′ ± v ′ (u \pm v) = u^{'} \pm v^{'} (u±v)=u′±v′
- ( c u ) ′ = c u ′ (cu)^{'} = cu^{'} (cu)′=cu′
- ( u v ) ′ = u ′ v + u v ′ (uv)^{'} = u^{'}v+uv^{'} (uv)′=u′v+uv′
- ( u v ) ′ = u ′ v − u v ′ v 2 ({u\over v})' = {{u^{'}v - uv^{'}} \over v^{2}} (vu)′=v2u′v−uv′
- ( 1 v ) ′ = 1 v 2 ({1\over v})^{'} = {1 \over v^{2}} (v1)′=v21
复合函数求导
若有两个一元函数
f
(
x
)
f(x)
f(x)、
g
(
x
)
g(x)
g(x)，可以将
g
g
g 的函数值作为
f
f
f 的自变量，得到一个新的函数称为
f
(
x
)
f(x)
f(x)、
g
(
x
)
g(x)
g(x) 的符合函数，记作
f
[
g
(
x
)
]
f[g(x)]
f[g(x)]，其导数为：
f
[
g
(
x
)
]
=
f
′
[
g
(
x
)
]
g
′
(
x
)
f[g(x)] = f^{'}[g(x)]g^{'}(x)
f[g(x)]=f′[g(x)]g′(x)
例如对于
y
=
s
i
n
(
2
x
)
y = sin(2x)
y=sin(2x) 函数求导，可以分解为
g
(
x
)
=
2
x
g(x) = 2x
g(x)=2x，
f
(
x
)
=
s
i
n
[
g
(
x
)
]
f(x) = sin[g(x)]
f(x)=sin[g(x)]，则：
f
′
(
x
)
=
x
c
o
s
(
2
x
)
f^{'}(x) = xcos(2x)
f′(x)=xcos(2x)
偏导数
偏导数是指一个多元函数对其中一个自变量求导，而保持其他变量恒定，记作：
∂
f
∂
x
\partial f \over \partial x
∂x∂f
例如对于
f
(
x
,
y
)
=
x
2
+
y
2
+
2
x
y
f(x,y) = x^{2} + y^{2} + 2xy
f(x,y)=x2+y2+2xy，对
x
x
x 求偏导数，可以将
y
y
y 看为常量:
∂
f
∂
x
(
x
,
y
)
=
2
x
+
2
y
{\partial f \over \partial x}(x,y) = 2x + 2y
∂x∂f(x,y)=2x+2y
