491.递增子序列

491. 递增子序列 

这道题的特点是有序的子序列(不能对原数组排序)，最终结果集res不能有重复子集。所以这道题又是子集又是去重

回溯三部曲

1.递归函数参数

本题求子序列，很明显一个元素不能重复使用，所以需要startIndex，调整下一层递归的起始位置。

2.终止条件

本题其实类似求子集问题，也是要遍历树形结构找每一个节点，所以和回溯算法：求子集问题！ (opens new window)一样，可以不加终止条件，startIndex每次都会加1，并不会无限递归。

但本题收集结果有所不同，题目要求递增子序列大小至少为2

3.递归逻辑

 在图中可以看出，同一父节点下的同层上使用过的元素就不能再使用了

代码实现

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        // 找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。
        backtracking(nums,0);
        return res;
    }
    public void backtracking(int[] nums,int startIndex){
        int[] used=new int[200];//因为题目给定范围是-100~100，这里范围0~200,可以使用一个used数组来记录同层元素是否被取过
        
        //本题其实类似求子集问题，也是要遍历树形结构找每一个节点，所以和回溯算法：求子集问题！ 78.子集一样，可以不加终止条件，因为startIndex每次会+1，而不是从0开始
        if(path.size()>1){
            res.add(new ArrayList<>(path));
            
        }
        for(int i=startIndex;i<nums.length;i++){
            if((!path.isEmpty()&&nums[i]<path.get(path.size()-1))||used[nums[i]+100]==1){//或者是同树层下使用到了相同元素
                continue;
            }
            used[nums[i]+100]=1;
            path.add(nums[i]);
            backtracking(nums,i+1);//这里是i+1，开始写错成startIndex+1
            //
            path.removeLast();
            

        }


    }
}

46.全排列

46. 全排列

这里和77.组合问题，131.切割问题和78.子集问题最大不同就算for循环里不用startIndex了。因为排列问题，每次都要从头开始搜索数组的

• 单层搜索的逻辑

这里和77.组合问题 (opens new window)、131.切割问题 (opens new window)和78.子集问题 (opens new window)最大的不同就是for循环里不用startIndex了。

因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。

而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。

 代码实现

class Solution {
    List<List<Integer>> res=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        // 给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列
         boolean[] used=new boolean[nums.length];
        backtracking(nums,used);
        return res;

    }
    public void backtracking(int[] nums,boolean[] used){
       
        //终止条件
        if(path.size()==nums.length){
            res.add(new ArrayList<>(path));//存放结果
            return;

        }
        //递归逻辑
        for(int i=0;i<nums.length;i++){
            if(used[i]==true){continue;}
            path.add(nums[i]);
            used[i]=true;//标记这个元素被使用过了，一个排列里一个元素只能用1次
            backtracking(nums,used);
            path.removeLast();
            used[i]=false;

        }
    }
}

大家此时可以感受出排列问题的不同：

• 每层都是从0开始搜索而不是startIndex
• 需要used数组记录path里都放了哪些元素了

47.全排列II

这道题相比46区别就是此题的nums数组中可以有重复元素

这道题涉及到的要解决的问题是排列+去重

排列参考46. 去重参考40组合总和II.90.子集II

递归搜索的逻辑：

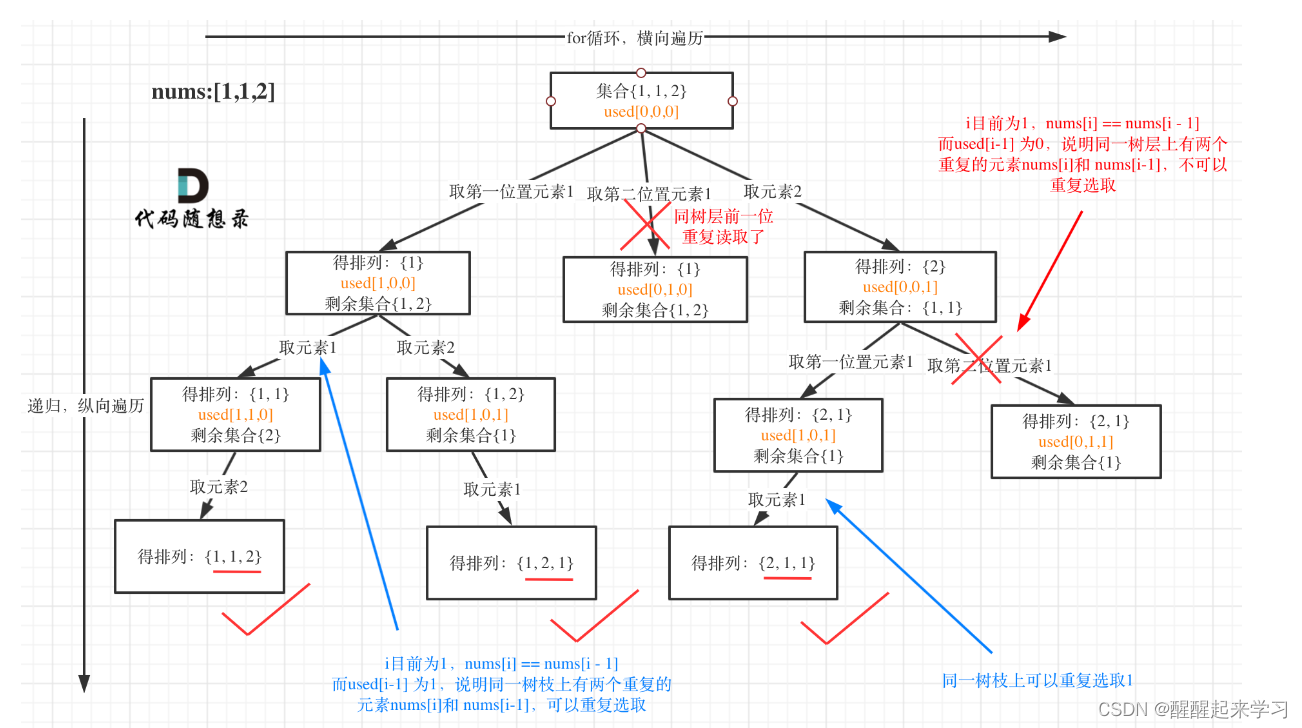
调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

我以示例中的 [1,1,2]为例 （为了方便举例，已经排序）抽象为一棵树，去重过程如图：

 

代码实现

//按任意顺序 返回所有不重复的全排列。说明需要进行去重
class Solution {
    List<List<Integer>> res=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used=new boolean[nums.length];
        Arrays.sort(nums);
        backtraccking(nums,used);
        return res;
    }
    public void backtraccking(int[] nums,boolean[] used){
        //终止条件，path大小和nums大小相同，把path添加到res中
        if(nums.length==path.size()){
            res.add(new ArrayList<>(path));
            return;
        }
       
        for(int i=0;i<nums.length;i++){
             //同层不能选相同的数字
             // used[i - 1] == true，说明同一树枝nums[i - 1]使用过
            // used[i - 1] == false，说明同一树层nums[i - 1]使用过
            // 如果同一树层nums[i - 1]使用过则直接跳过，这里和46.题不同
            if(i>0&&nums[i]==nums[i-1]&&!used[i-1]){
                continue;
                
            }
            if(used[i]==false){//加上这个判断，这里和46.题不同
            used[i]=true;
            path.add(nums[i]);
            
            backtraccking(nums,used);//回溯
            used[i]=false;
            path.removeLast();
            }


        }
    }
}

今天在做回溯的过程还是很容易懵逼，加油。