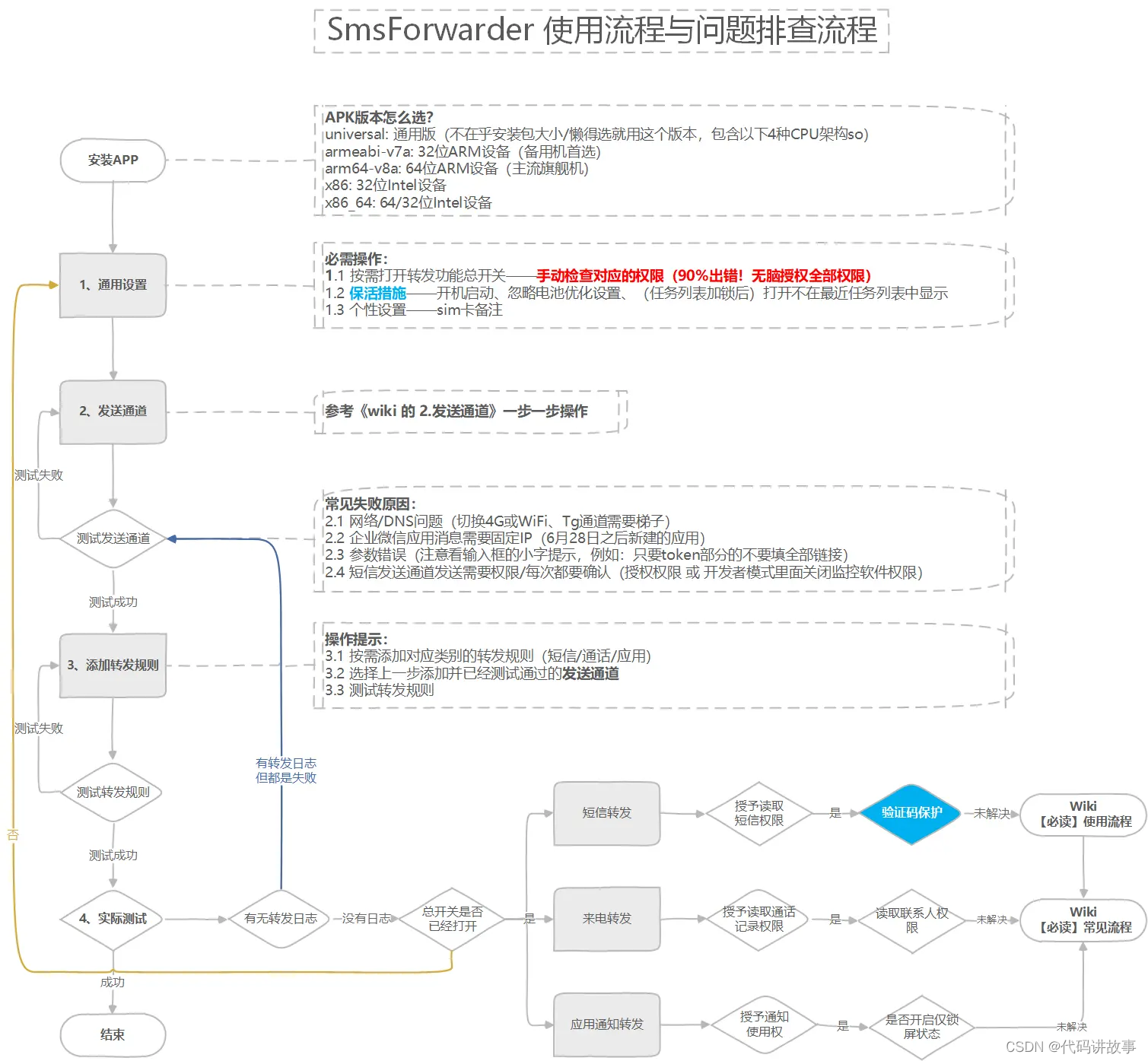
大家好,我是半虹,这篇文章来讲长短期记忆网络 (Long Short-Term Memory, LSTM)
文章行文思路如下:
- 首先通过循环神经网络引出为啥需要长短期记忆网络
- 然后介绍长短期记忆网络的核心思想与运作方式
- 最后通过简短的代码深入理解长短期记忆网络的运作方式
长短期记忆网络可以看作是循环神经网络的改进版本,想要理解长短期记忆网络,首先要了解循环神经网络
由于我们之前已详细介绍过循环神经网络,所以这里我们只会做一个简单的回顾,想看详细的说明请戳这里
对比前馈神经网络,循环神经网络通过增加隐状态实现对隐藏层信息的传递,以此达到记住历史输入的目的
网络在每个时间步里读取上一隐藏层输出作为当前隐藏层输入,并保存当前隐藏层输出作为下一隐藏层输入
其结构简图如下:

其中 X X X 是输入 , H H H 是隐藏层的输出,图中的每个矩形都表示同一个循环神经网络隐藏层
下面我们把隐藏层中的细节也画出来,方便后面与长短期记忆网络来对比

其中 X X X 是输入 , H H H 是隐藏层的输出,图中的灰色矩形同样代表隐藏层, σ \sigma σ 表示一个带激活函数的线性层
对应的公式表达如下:
H
t
=
α
(
X
t
W
x
h
+
H
t
−
1
W
h
h
+
b
h
)
H_{t} = \alpha(X_{t} W_{xh} + H_{t-1} W_{hh} + b_{h})
Ht=α(XtWxh+Ht−1Whh+bh)
其中
X
t
X_{t}
Xt 是当前输入,
H
t
H_{t}
Ht 是当前隐藏层输出,
H
t
−
1
H_{t-1}
Ht−1 是先前隐藏层输出,
W
x
h
W_{xh}
Wxh、
W
h
h
W_{hh}
Whh 和
b
h
b_{h}
bh 都是网络参数
理论上,上述介绍的循环神经网络能处理任意长的序列,但实际上却并非如此
在实际应用循环神经网络处理长序列时通常会出现梯度爆炸或梯度消失的情况,导致网络难以捕捉长期依赖
这是为什么呢?通过简单分析一下梯度计算公式就能发现端倪
为了阐述方便,我们暂且假定所有的参数都是一维的,用字母
θ
\theta
θ 表示,对参数求导并按时间展开后如下所示
d
H
t
d
θ
=
∂
H
t
∂
θ
+
∂
H
t
∂
H
t
−
1
d
H
t
−
1
d
θ
=
∂
H
t
∂
θ
+
∂
H
t
∂
H
t
−
1
∂
H
t
−
1
∂
θ
+
∂
H
t
∂
H
t
−
1
∂
H
t
−
1
∂
H
t
−
2
d
H
t
−
2
d
θ
+
⋯
\begin{align*} \frac{d H_{t}}{d \theta} &= \frac{\partial H_{t}}{\partial \theta} + \frac{\partial H_{t}}{\partial H_{t-1}} \frac{d H_{t-1}}{d \theta} \\ &= \frac{\partial H_{t}}{\partial \theta} + \frac{\partial H_{t}}{\partial H_{t-1}} \frac{\partial H_{t-1}}{\partial \theta} + \frac{\partial H_{t}}{\partial H_{t-1}} \frac{\partial H_{t-1}}{\partial H_{t-2}} \frac{d H_{t-2}}{d \theta} + \cdots \end{align*}
dθdHt=∂θ∂Ht+∂Ht−1∂HtdθdHt−1=∂θ∂Ht+∂Ht−1∂Ht∂θ∂Ht−1+∂Ht−1∂Ht∂Ht−2∂Ht−1dθdHt−2+⋯
不难发现,当前梯度
d
H
t
d
θ
\frac{d H_{t}}{d \theta}
dθdHt 由当前梯度值
∂
H
t
∂
θ
\frac{\partial H_{t}}{\partial \theta}
∂θ∂Ht 以及先前梯度
d
H
t
−
1
d
θ
\frac{d H_{t-1}}{d \theta}
dθdHt−1 决定,对于先前梯度权重
∂
H
t
∂
H
t
−
1
\frac{\partial H_{t}}{\partial H_{t-1}}
∂Ht−1∂Ht:
- 当 ∣ ∂ H t ∂ H t − 1 ∣ < 1 |\frac{\partial H_{t}}{\partial H_{t-1}}| < 1 ∣∂Ht−1∂Ht∣<1 时,表示历史的梯度信息是逐渐减弱的,随着时间步不断增加,很可能会出现梯度消失
- 当 ∣ ∂ H t ∂ H t − 1 ∣ > 1 |\frac{\partial H_{t}}{\partial H_{t-1}}| > 1 ∣∂Ht−1∂Ht∣>1 时,表示历史的梯度信息是逐渐增强的,随着时间步不断增加,很可能会出现梯度爆炸
由推导式可以看出,梯度爆炸和梯度消失更容易出现在与当前时间步距离更远的梯度
这是因为这些梯度的权重连乘项更多,举例来说,对于时间步 t t t,其梯度 d H t d θ \frac{d H_{t}}{d \theta} dθdHt 由以下梯度相加组成
- 时间步 t − 1 t - 1 t−1 的梯度 d H t − 1 d θ \frac{d H_{t-1}}{d \theta} dθdHt−1,与时间步 t t t 的距离为 1 1 1,其权重为 ∂ H t ∂ H t − 1 \frac{\partial H_{t}}{\partial H_{t-1}} ∂Ht−1∂Ht
- 时间步 t − 2 t - 2 t−2 的梯度 d H t − 2 d θ \frac{d H_{t-2}}{d \theta} dθdHt−2,与时间步 t t t 的距离为 2 2 2,其权重为 ∂ H t ∂ H t − 1 ∂ H t − 1 ∂ H t − 2 \frac{\partial H_{t}}{\partial H_{t-1}} \frac{\partial H_{t-1}}{\partial H_{t-2}} ∂Ht−1∂Ht∂Ht−2∂Ht−1
- 时间步 t − 3 t - 3 t−3 的梯度 d H t − 2 d θ \frac{d H_{t-2}}{d \theta} dθdHt−2,与时间步 t t t 的距离为 3 3 3,其权重为 ∂ H t ∂ H t − 1 ∂ H t − 1 ∂ H t − 2 ∂ H t − 3 ∂ H t − 3 \frac{\partial H_{t}}{\partial H_{t-1}} \frac{\partial H_{t-1}}{\partial H_{t-2}} \frac{\partial H_{t-3}}{\partial H_{t-3}} ∂Ht−1∂Ht∂Ht−2∂Ht−1∂Ht−3∂Ht−3
- ……
这说明了什么?这说明了对于当前输入,距其更远的输入的梯度更容易出现梯度爆炸或梯度消失
从而导致长距离的梯度反馈失效,这就是循环神经网络难以捕捉长期依赖的实际含义
最后提醒大家注意一个细节,对于时间步 t t t 的梯度 d H t d θ \frac{d H_{t}}{d \theta} dθdHt:
- 假设有且仅有最后一项梯度爆炸,那么就会导致整个梯度爆炸,因为 d H t − 1 d θ + ⋯ + N a N = N a N \frac{d H_{t-1}}{d \theta} + \cdots + NaN = NaN dθdHt−1+⋯+NaN=NaN
- 假设有且仅有最后一项梯度消失,这并不会导致整个梯度消失,因为 d H t − 1 d θ + ⋯ + 0 ≠ 0 \frac{d H_{t-1}}{d \theta} + \cdots + 0 \neq 0 dθdHt−1+⋯+0=0
总结一下,梯度反向传播时发生的异常,主要可以分为两种,一是梯度爆炸,二是梯度消失
梯度爆炸比较容易处理,一个简单但有效的做法是设置一个梯度阈值,当梯度超过这个阈值时直接截断
梯度消失更难处理一些,而现在流行的做法正是将循环神经网络替换成长短期记忆网络
注意,长短期记忆网络能缓解梯度消失的问题,但并不能缓解梯度爆炸的问题
上面我们从反向传播的角度解释了什么是梯度消失
如果我们从前向计算的角度来看,则梯度消失可以理解成隐状态对短期记忆敏感,对长期记忆作用有限
为了维持长期记忆,长短期记忆网络引入记忆元存放长期记忆,并通过门机制控制记忆元中的信息流动
从直觉上来说,先前重要的记忆会保留在记忆元,不重要的记忆会被过滤,以此来达到长期记忆的目的
这里有两个概念需要解释,一是记忆元,二是门机制,这两个就是长短期记忆网络的核心
先说记忆元,可以理解成另一种隐状态,都是用来记录附加信息的,简称为单元,英文为 Cell \text{Cell} Cell
再说门机制,这是用来控制记忆元中信息流动的机制,具体来说包括三个控制门:
- 输入门:控制是否将信息写入记忆元,英文为 Input Gate \text{Input Gate} Input Gate
- 遗忘门:控制是否从记忆元丢弃信息,英文为 Forget Gate \text{Forget Gate} Forget Gate
- 输出门:控制是否从记忆元读出信息,英文为 Output Gate \text{Output Gate} Output Gate
本质上来说,上述三个控制门都是由一个线性层加一个激活函数组成的,这里激活函数用的是 sigmoid \text{sigmoid} sigmoid
因为这样能将输出限制在零到一之间,以表示门的打开程度,控制信息流动的程度
相比循环神经网络只有一个传输状态,即隐状态,长短期记忆网络有两个传输状态,即隐状态和记忆元
二者的输入输出对比图如下:

其中 H H H 表示隐状态, C C C 表示记忆元,知道输入输出后,下面开始介绍长短期记忆网络的内部工作原理
首先,根据当前输入 X t X_{t} Xt 和先前隐状态 H t − 1 H_{t-1} Ht−1,计算得到输入门 I t I_t It、遗忘门 F t F_t Ft、输出门 O t O_t Ot
其中,
W
x
i
W_{xi}
Wxi、
W
h
i
W_{hi}
Whi、
b
i
b_{i}
bi、
W
x
f
W_{xf}
Wxf、
W
h
f
W_{hf}
Whf、
b
f
b_{f}
bf、
W
x
o
W_{xo}
Wxo、
W
h
o
W_{ho}
Who、
b
o
b_{o}
bo 都是网络参数,
σ
\sigma
σ 是
sigmoid
\text{sigmoid}
sigmoid 激活函数
I
t
=
σ
(
X
t
W
x
i
+
H
t
−
1
W
h
i
+
b
i
)
F
t
=
σ
(
X
t
W
x
f
+
H
t
−
1
W
h
f
+
b
f
)
O
t
=
σ
(
X
t
W
x
o
+
H
t
−
1
W
h
o
+
b
o
)
\begin{align*} I_{t} &= \sigma (X_{t} W_{xi} + H_{t-1} W_{hi} + b_{i}) \\ F_{t} &= \sigma (X_{t} W_{xf} + H_{t-1} W_{hf} + b_{f}) \\ O_{t} &= \sigma (X_{t} W_{xo} + H_{t-1} W_{ho} + b_{o}) \end{align*}
ItFtOt=σ(XtWxi+Ht−1Whi+bi)=σ(XtWxf+Ht−1Whf+bf)=σ(XtWxo+Ht−1Who+bo)
然后,根据当前输入 X t X_{t} Xt 和先前隐状态 H t − 1 H_{t-1} Ht−1,计算得到候选记忆元 C ~ t \widetilde{C}_{t} C t
其中,
W
x
c
W_{xc}
Wxc、
W
h
c
W_{hc}
Whc、
b
c
b_{c}
bc 都是网络参数,
tanh
\tanh
tanh 是
tanh
\tanh
tanh 激活函数
C
~
t
=
tanh
(
X
t
W
x
c
+
H
t
−
1
W
h
c
+
b
c
)
\widetilde{C}_{t} = \tanh (X_{t} W_{xc} + H_{t-1} W_{hc} + b_{c})
C
t=tanh(XtWxc+Ht−1Whc+bc)
接着,输入门
I
t
I_t
It 控制采用多少来自
C
~
t
\widetilde{C}_{t}
C
t 的新信息,遗忘门
F
t
F_t
Ft 控制保留多少来自
C
t
−
1
C_{t-1}
Ct−1 的旧信息,计算得
C
t
C_t
Ct
其中,
⊙
\odot
⊙ 表示按元素乘法,当
I
t
=
0
I_{t} = 0
It=0 且
F
t
=
1
F_{t} = 1
Ft=1 时,则过去记忆元被保留并传递到当前时间步
C
t
=
F
t
⊙
C
t
−
1
+
I
t
⊙
C
~
t
C_{t} = F_{t} \odot C_{t-1} + I_{t} \odot \widetilde{C}_{t}
Ct=Ft⊙Ct−1+It⊙C
t
最后,输出门
O
t
O_t
Ot 控制采用多少来自
C
t
C_{t}
Ct 的长记忆,计算得
H
t
H_{t}
Ht
其中,
⊙
\odot
⊙ 表示按元素乘法,
tanh
\tanh
tanh 表示
tanh
\tanh
tanh 激活函数,当
O
t
O_{t}
Ot 接近
1
1
1 时,就可以将长期记忆传递给隐状态
H
t
=
O
t
⊙
tanh
(
C
t
)
H_{t} = O_{t} \odot \tanh (C_{t})
Ht=Ot⊙tanh(Ct)
上述计算过程对应的计算图如下所示:

为了帮助大家进一步理解长短期记忆网络的工作方式,下面我们举一个例子来说,并给出关键代码
假设我们用长短期记忆网络对下面这个句子进行编码:我在画画
import torch
import torch.nn as nn
# 定义输入数据
# 对于输入句子我在画画,首先用独热编码得到其向量表示
x1 = torch.tensor([1, 0, 0]).float() # 我
x2 = torch.tensor([0, 1, 0]).float() # 在
x3 = torch.tensor([0, 0, 1]).float() # 画
x4 = torch.tensor([0, 0, 1]).float() # 画
h0 = torch.zeros(5) # 初始化隐状态
c0 = torch.zeros(5) # 初始化记忆元
# 定义模型参数
# 模型的输入是三维向量,这里定义模型的输出是五维向量
W_xi = nn.Parameter(torch.randn(3, 5), requires_grad = True)
W_hi = nn.Parameter(torch.randn(5, 5), requires_grad = True)
b_i = nn.Parameter(torch.randn(5) , requires_grad = True)
W_xf = nn.Parameter(torch.randn(3, 5), requires_grad = True)
W_hf = nn.Parameter(torch.randn(5, 5), requires_grad = True)
b_f = nn.Parameter(torch.randn(5) , requires_grad = True)
W_xo = nn.Parameter(torch.randn(3, 5), requires_grad = True)
W_ho = nn.Parameter(torch.randn(5, 5), requires_grad = True)
b_o = nn.Parameter(torch.randn(5) , requires_grad = True)
W_xc = nn.Parameter(torch.randn(3, 5), requires_grad = True)
W_hc = nn.Parameter(torch.randn(5, 5), requires_grad = True)
b_c = nn.Parameter(torch.randn(5) , requires_grad = True)
# 前向传播
def forward(X, H, C):
# 计算输入门、遗忘门、输出门
I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)
F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)
O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)
# 计算候选记忆元
C_tilde = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)
# 计算当前记忆元
C = F * C + I * C_tilde
# 计算当前隐状态
H = O * C.tanh()
# 返回结果
return H, C
h1, c1 = forward(x1, h0, c0)
h2, c2 = forward(x2, h1, c1)
h3, c3 = forward(x3, h2, c2)
h4, c4 = forward(x4, h3, c3)
# 结果输出
print(h3) # tensor([-0.0408, 0.1785, 0.0455, 0.3802, 0.0235])
print(h4) # tensor([-0.0560, 0.1269, 0.0346, 0.3426, 0.0118])
最后提醒大家一点,如果长短期记忆网络后有接其他网络,例如后面接一个线性层做单词预测
那么通常不会用记忆元的输出,而是用隐藏层的输出
至此本文结束,要点总结如下:
-
循环神经网络在处理长序列时很容易会出现梯度爆炸和梯度消失的情况,导致网络难以捕捉长期依赖
对于梯度爆炸,通常可以采用梯度裁剪解决,对于梯度消失,可以采用长短期记忆网络缓解
-
除了有隐状态,长短期记忆网络还增加记忆元存放长期记忆,并通过门机制控制记忆元中的信息流动