目录
- 一、缩放比例
- 二、方格化变换的基础
- 三、重建时间
- 四、方格化核
一、缩放比例
对于笛卡尔K空间直线轨迹数据可直接用FFT重建,而如果K空间轨迹的任何部分都是非均匀取样的 可用DFT直接重建,有时称为共轭相位重建,但此法太慢不实用。把数据再取样到直线格使能FFT重建要快得多。普遍应用的内插方法是把数据与一个平滑函数卷积再取样,这个 重建过程(包括FFT) 被称为 方格化。
方格化在K空间中用一个卷积转换输入数据到一个均匀直线格数据集,因自选密度本身是紧支的(即有限区域外都是零),只要测量值是大于或等于奈奎斯特频率采样的,任意位置的K空间值都可以被测量值的sinc内插精确计算(即测量的K空间值与sinc函数卷积)。
sinc内插的缺点是sinc函数不是紧支的。因此,在每个新K空间位置计算K空间值,要求sinc函数被所有测量的数据乘,导致比较长的计算时间。
在方格化中,sinc函数被一个紧支函数(方格化核)取代以节省计算时间。K空间数据与方格化核卷积等价于图像被核的FT乘。
sinc卷积方格化导致些许图像质量损失,因为再取样卷积的K空间导致一个带有混叠的图像。通常通过K空间过取样以增大FOV(把直线混叠的复制进一步推离开推向),以降低混叠,然后在FT后放弃额外的FOV。

左为模拟的spiral扫描图像,显示有混叠伪影。
混叠延申到无限远,即使显示的截面有限(方框是扫描中指定的FOV)。
右为从左图(尚无直线再取样)的K空间数据的内插产生的图像
如果对应于左图的K空间数据与一紧支函数而不是sinc卷积,混叠伪影就不会被截去。
径向投影MR数据也可以用CT中常用的滤波背投影算法,但此法在MRI中不受欢迎。对一个离散数据集再取样问题已经发展了许多方法,直接内插会导致伪影,基于卷积的方法比如方格化在MRI中被广泛使用,因为它比其他方法快,并且能给出足够好的图像质量。
所谓 两个函数的卷积,本质上就是先将一个函数翻转,然后进行滑动叠加。在连续情况下,叠加指的是对两个函数的乘积求积分,在离散情况下就是加权求和,为简单起见就统一称为叠加。卷积的“卷”,指的的函数的翻转,从 g(t) 变成 g(-t) 的这个过程;同时,“卷”还有滑动的意味在里面。如果把卷积翻译为“褶积”,那么这个“褶”字就只有翻转的含义了。卷积的“积”,则指的是积分/加权求和。
以信号分析为例,卷积的结果是不仅跟当前时刻输入信号的响应值有关,也跟过去所有时刻输入信号的响应都有关系,考虑了对过去的所有输入的效果的累积。在图像处理中,卷积处理的结果,其实就是把每个像素周边的,甚至是整个图像的像素都考虑进来,对当前像素进行某种加权处理。所以说,“积”是全局概念,或者说是一种“混合”,把两个函数在时间或者空间上进行混合。
进行“卷”(翻转)的目的其实是施加一种约束,它指定了在“积”的时候以什么为参照。在信号分析的场景,它指定了在哪个特定时间点的前后进行“积”,在空间分析的场景,它指定了在哪个位置的周边进行累积处理。
二、方格化变换的基础
方格化所需要的步骤为:
(1)对各个输入数据点计算K空间位置和密度补偿。
(2)计算方格化核及其反傅里叶变换,存储方格化核作为一个查找表或者对各个输入、输出数据样本存储值。
(3)如果需要,从输入数据减去基线。
(4)准备一个待输出K空间矩阵,对各个输入数据样本在输入点的紧支距离内找出所有均匀直线输出位置。
(5)应用一个K空间窗和符号交替到再取样的直线K空间数据上。
(6)反傅里叶变换均匀直线再取样的K空间数据上。
(7)如果K空间过取样用于降低混叠,提取图像的中间位置相应于所希望的最终FOV。
(8)用方格化核的反傅里叶变换除以中间像。
(9)如果需要实像或虚像,进行符号交替。
(10)计算最终图像,比例缩放。
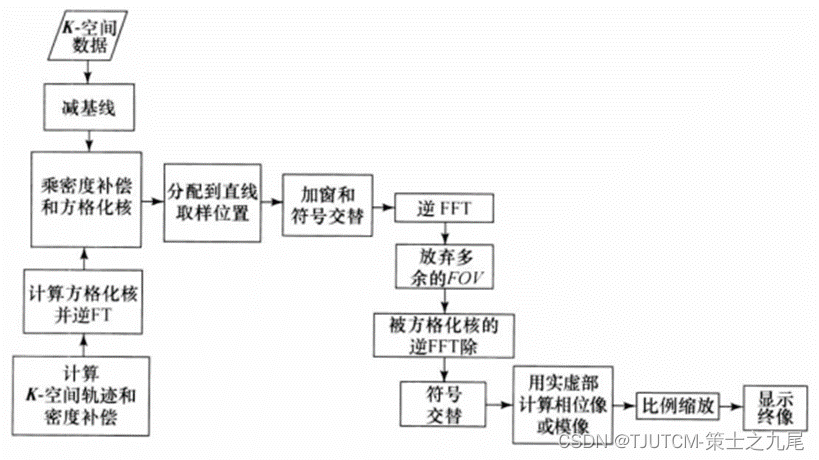
方格化是一个局部过程,只需在原取样点附近执行。
为了节省计算时间,方格化核值通常不再对各个输出点计算。方格化核值只对相对小数量点计算,比如256点,并存在一个查找表中。如果同样的K空间轨迹用于重复的重建,并且有足够多存储器的话,第一个像之后所有像的重建时间可通过查表而大大节省。
三、重建时间
方格化重建 可分为三步:卷积、FFT和被方格化核的IFT除。
卷积步乘法运算次数 是输入数据样本数Ns乘以位于各输入样本的距离w内的均匀直线位置数。如果w是用均匀直线样本的单位给定的,乘运算次数对于1D方格化是wNs,对2D方格化是w^2Ns,以此类推。
例如 在傅里叶变换中,一个复数函数的实部和虚部分别对应着信号的振幅和相位。如果一个信号的傅里叶变换F(k)的共轭F*(k)等于F(-k),那么这个信号的相位是对称的,即F(k)和F*(k)相位相等。相位信息可以用来描述信号的时间演化和频率成分。
受敲击的鼓面振幅沿半径方向的分布就是一个贝塞尔函数(考虑正负号)。实际上,这些振动是各阶贝塞尔函数的叠加。
根据图像阵列的特性,对其按下列步骤进行FFT变换:
(1)将图像数据阵列变换为按列存储,即从下到上,从左到右;
(2)对每一列图像数据进行1-D FFT;
(3)将按列处理后的数据结果存储,并对它们按原图像阵列的形式,即按行重新存储;
(4)对重新排列的数据逐行进行1-D FFT;
(5)将每行处理后的数据存储起来,即得到2-D 数字图像FFT结果。
关于离散傅里叶变换变换:
(1)实数信号变换的结果X[k]是一组复数,里面一半数据和另一半是共轭的。意味着N点DFT,只有N/2的数据是含有有用信息的。
(2)用DFT的结果如何做频谱分析,即在采样频率为fs的情况下, x[n]的n只是一个离散的数值。
四、方格化核
最佳1D方格化核g(K)是Kaiser-Bessel函数,在终像最逼近理想像(例如用共轭相位重建)的意义上说,Kaiser-Bessel函数作为方格化核能给出最佳结果。
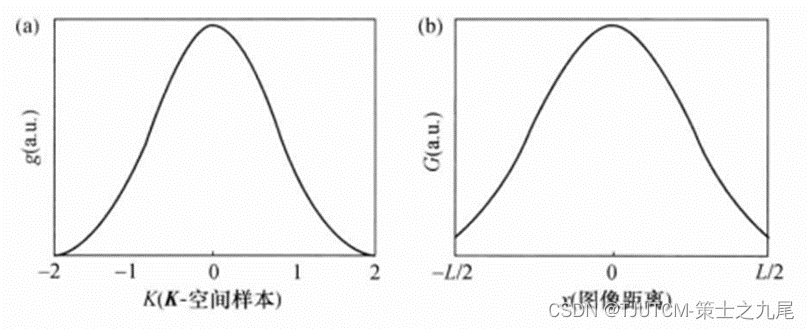
(a)图为Kaiser-Bessel函数(任意单位)作为K空间距离(以K空间为单位)的函数
(b)图为Kaiser-Bessel函数(任意单位)的反傅里叶变换曲线作为图像视野L的函数,Kaiser-Bessel函数参数w=4,b=8