上结论：

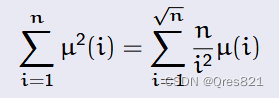
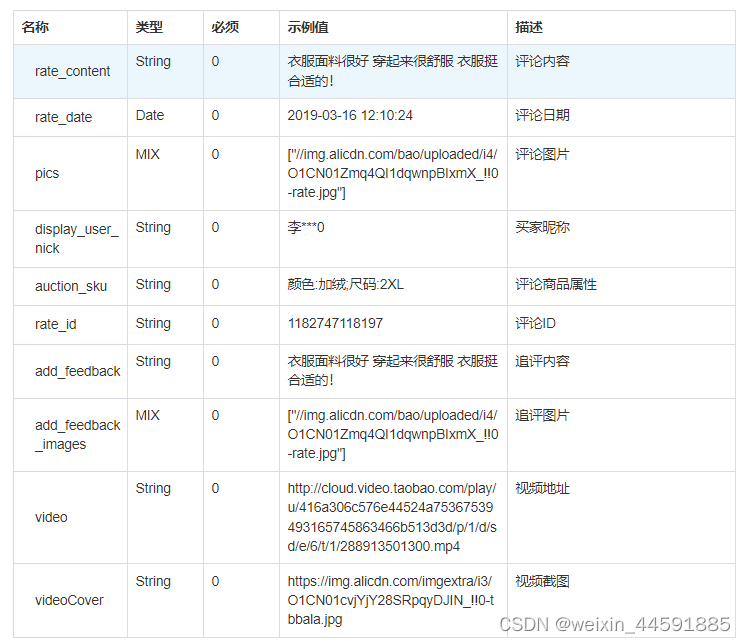
左边式子的本质就是 $n$ 以内有多少个数没有平方因子

然后我们枚举所有平方因子 $i^2$，包含它的有 $\frac{n}{i^2}$ 个

右边本质是一个容斥，首先所有数都有平方因子 $1^2$，然后类似 $2^2,3^2$ 这类要减掉，有些重复减的要加上，例如 $6^2$。而像 $4^2,9^2$ 的 $\mu (i)=0$，所以不会被统计