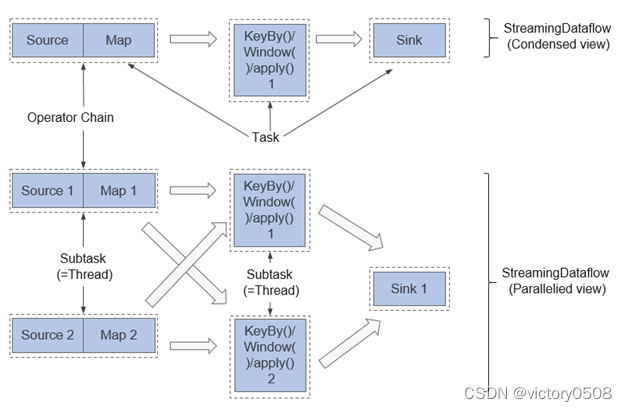
一、基础概念(学习笔记)
(1)训练误差和泛化误差[1]
本质上,优化和深度学习的目标是根本不同的。前者主要关注的是最小化目标,后者则关注在给定有限数据量的情况下寻找合适的模型。训练误差和泛化误差通常不同:由于优化算法的目标函数通常是基于训练数据集的损失函数,因此优化的目标是减少训练误差。但是,深度学习(或更广义地说,统计推断)的目标是减少泛化误差。
最小化训练误差并不能保证我们找到最佳的参数集来最小化泛化误差。同时,对于深度学习而言,没有必要找到最优解,局部最优解或其近似解仍然非常有用。
个人理解:训练误差为训练集每个Epoch的损失,泛化误差为验证集对应Epoch的损失。训练集与验证集的精确率曲线对比可以作为验证模型是否过拟合的标志。一段时间内的训练集Epoch精确率曲线不断升高且验证集Epoch精确率曲线不断降低,即很大可能模型过拟合了。
(2)Python变量[10]
Python变量由内存地址标识、数据类型、变量值组成。标识对象所存储的内存地址,使用内置函数id(obj)来获取;对象的数据类型,使用内置函数type(obj)来获取。
Python的一切变量都是对象,都采用了引用语义的方式存储,存储的只是一个变量的值所在的内存空间,Python的变量创建、赋值操作可基于C中的指针理解。在Python中需要使用到变量值时,变量会根据自身存储的指向值的内存地址从而获取值。
(3)可迭代对象、迭代器和生成器(Python机制)[7][8]
可迭代对象(Iterable),指存储了元素的一个容器对象,且容器中的元素可以通过__iter__()方法(迭代器形式返回)或__getitem__()方法(实例名[index])访问。
迭代器(Iterator),迭代器可以看作是一个特殊的对象,每次调用该对象时会返回自身的下一个元素(调入内存)。从类构造上来看,一个迭代器对象必须是定义了__iter__()方法和next()方法的对象。迭代器的优点是节约内存(数据循环读入内存而不是一次性,同时每次取值上一条数据都会在内存释放)、实现惰性计算(需要时再根据保存的状态计算读入对应数据),缺点是只能向前一个个访问数据、已访问数据无法再次访问、迭代访问一轮后迭代器空置。
生成器(Generator),本质上还是一种迭代器,但其倾向于存在计算过程的迭代器。生成器包含yield关键字,同时也可使用next()获取数据。对比于列表生成式(实例 = [F(x)for x in iterable])返回一个关于F(x)的函数值列表,将[]替换为()即可转换为一个生成器。
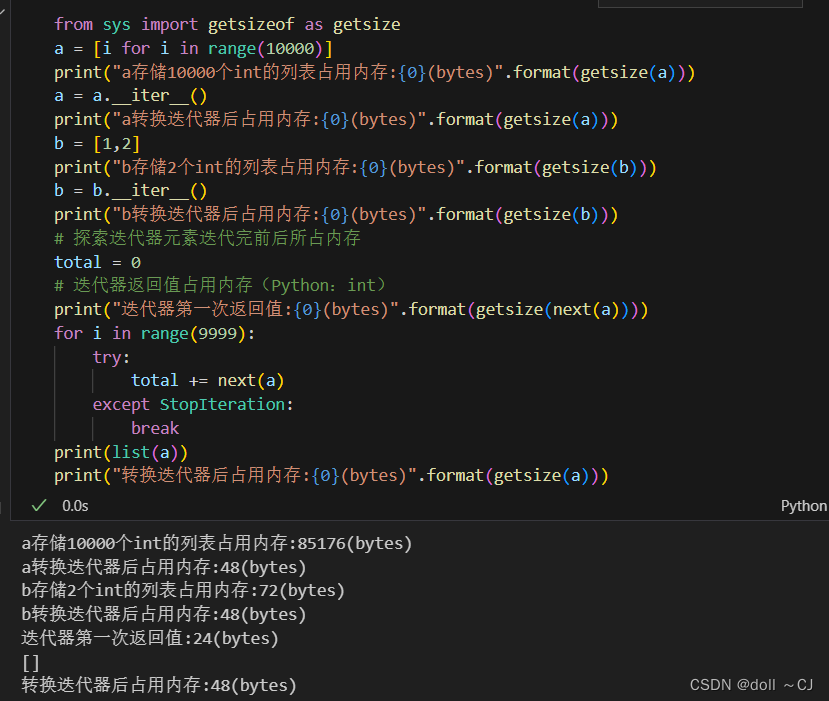

显然,通过实验可以发现:
(1)若列表存储大量数值且不需要一次性全部参与计算,那么将其转换为迭代器逐次加入内存,可以节省大量的内存空间(迭代器的内存占用空间不变);
(2)在Python中,int数字变量是变长存储,其最小内存占用为24Bytes。通过查阅资料,Python基于C语言编成,但Python的int是动态的,其int是一个类,类内包含特殊的数据结构。
(3)getsize()仅返回对象的内存占用大小(仅考虑直接归因于该对象的内存消耗,而不考虑其引用的对象的内存消耗)。对于容器对象(例如字典或列表),给定的内存大小仅涵盖容器使用的内存以及用于引用其他对象的指针值。如果需要计算容器的内存占用以及该容器引用所有内容的大小,必须自己编程实现遍历这些包含对象并获取他们大小。
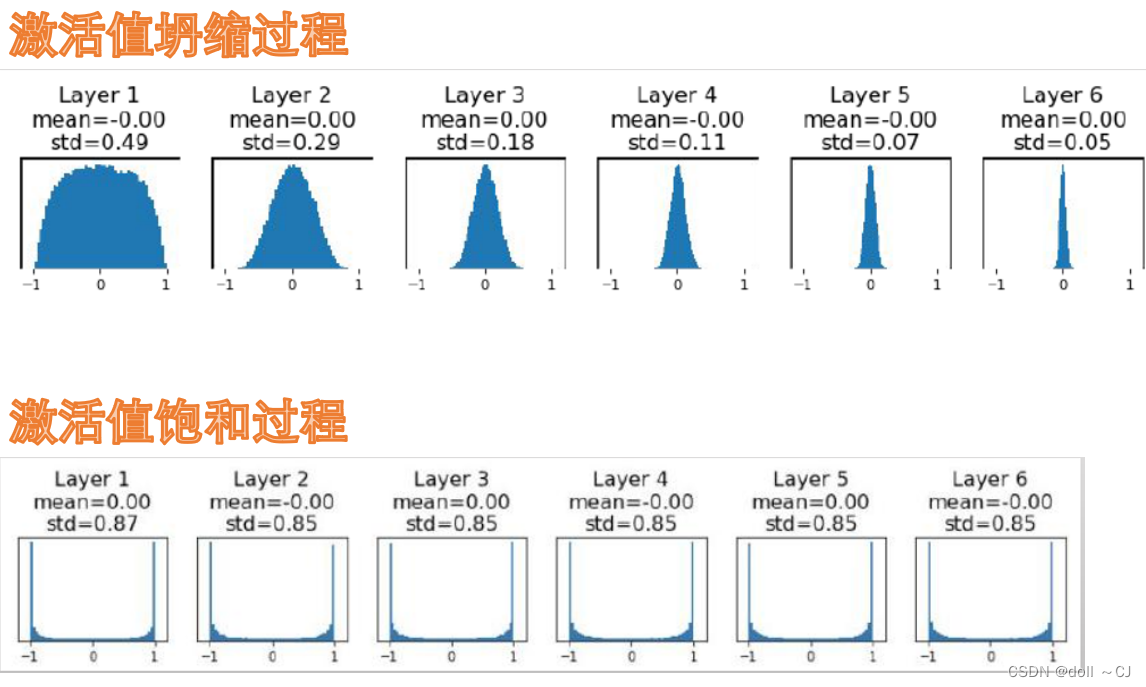
(4)权重初始化Weight Initialization(常用方法)[11]
Xavier与 Kaiming权重参数初始化

上述初始化方式,尽可能地保证了训练较长时期的输入激活值都没有出现坍缩或饱和现象,使得网络中的信息得到了较好的流动。
(5)数据归一化处理
数据归一化的优点,一是对权值的微小变化不太敏感,更易于优化;二是一定程度上减少了数据内存消耗。
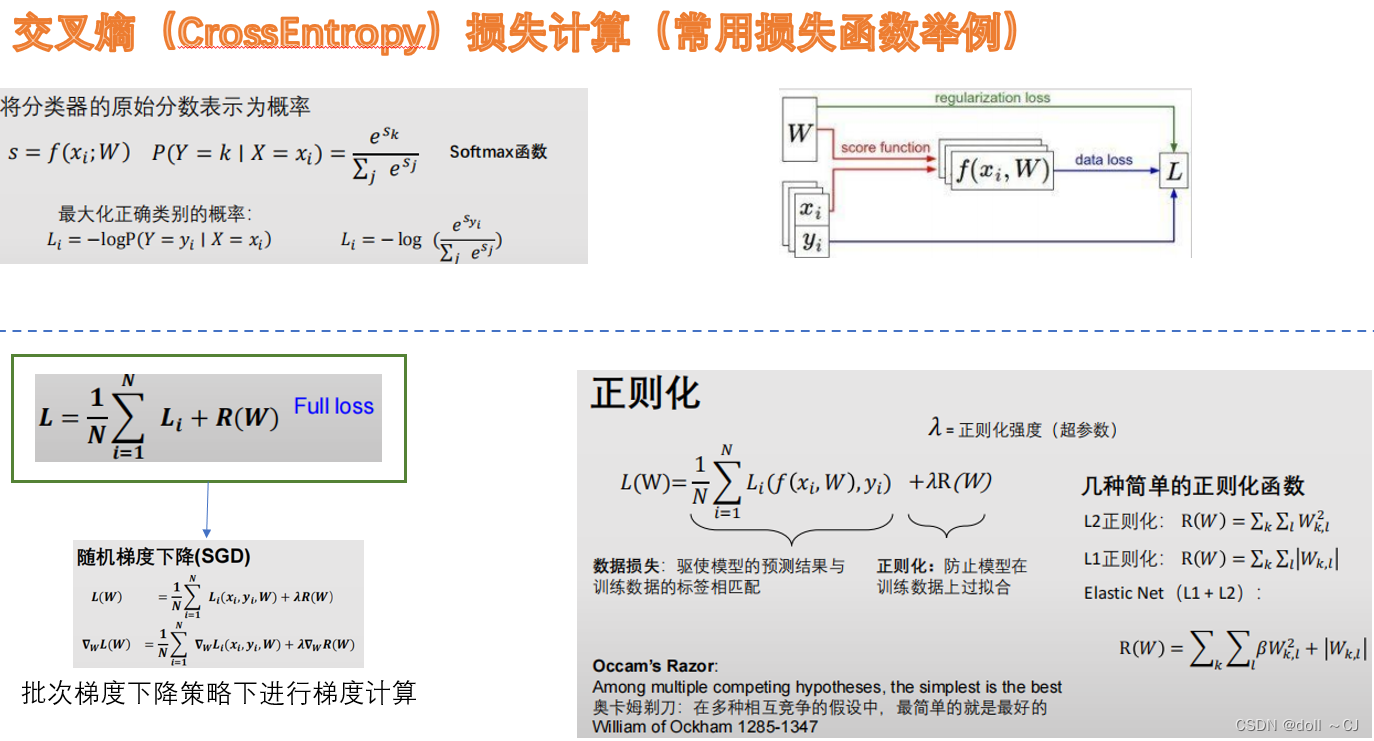
(6)损失函数
常见的损失函数有交叉熵损失、Hinge损失、平方误差损失等,其中针对样本不平衡情况也涌现出了较多的基于损失函数Trick的缓解方法。具体详细的关于损失函数的内容可见本文参考资料[14]。
(7)梯度下降(gradient descent)
在深度学习(神经网络)模型中,BP反向传播方法的核心就是对每层的权重参数不断使用梯度下降来进行优化 [13] 。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向。在深度学习中,计算图使得反向传播算法实现变得简单。
小批量随机梯度下降(minibatch gradient descent)是目前常用的梯度下降策略。其在多次训练迭代之后,几乎能与使用完整数据集来计算梯度的模型精确率相近并避免了全读入的内存限制问题。同时,其缓解了单个观测值处理频繁随机梯度下降(随机梯度下降—SGD),频繁更新权重参数造成的大量耗时。

(8)学习率调整策略——WarmUp+
Warmup是一种学习率预热方法,在模型最初几个Epoch以较低学习率训练,后又改为预先设置的学习率以及调整策略进行训练。由于刚开始训练时,模型的权重是随机初始化的,此时若选择一个较大的学习率,可能使得模型学偏或不稳定(最初的更新方向可能也是毫无意义的)。而Warmup可以在训练初期使模型相对趋于稳定后再选择常见策略训练,从而更大可能使得模型收敛速度变快、模型效果更佳 [5]。
常见的学习率调整策略有分段常数衰减、指数衰减、余弦衰减、分段衰减、余弦退火、周期三角、warmup以及多种组合策略。本文主要针对warmup+其它学习率调整策略组合进行实现。若需要更为详细地了解学习率调整策略可参考本文参考资料[1][2][3][5]。
二、基于Jupyter的Pytorch自定义模型方法实践
(一)Pytorch自定义数据集读取类(父类Dataset)[6]
Dataset自定义设计,主要就是重写__len__()和__getitem__()两个成员函数。同时,我们可以在__getitem__()函数中加入对样本数据的预处理,该操作通常可以借助Torchvision.transforms包含的类操作。
值得注意的是:
1)样本及其对应标签样本数据的良好命名可以使得数据读入更为规范;
2)将图像样本数据归一化到0-1内可以节省内存;
3)对于标签数据,我们通常遵循类别从0-n(整型int)顺序标记为规范,将耕地标签改为1便于后续作交叉熵计算。
class MyDataset(Dataset):
def __init__(self, imgPath, biaoqianPath):
self.imgPath = imgPath
self.biaoqianPath = biaoqianPath
self.imgName = os.listdir(imgPath)
# ToTensor会将数据归一化到0-1之间
self.preProcess = ToTensor()
def __len__(self):
return len(self.imgName)
def __getitem__(self, index):
imgP = os.path.join(self.imgPath, self.imgName[index])
biaoqianP = os.path.join(self.biaoqianPath, r"{0}_mask.png".format(self.imgName[index].split(".")[0]))
# 读入单张图片数据为 H-W-C 即256×256×3
img = cv2.imread(imgP)
biaoqian = cv2.imread(biaoqianP)
biaoqianGray = cv2.cvtColor(biaoqian, cv2.COLOR_BGR2GRAY)
# 将耕地标签255更改为1(为规范化)
biaoqianGray = biaoqianGray // 255
# 样本多波段数据归一化
img = self.preProcess(img)
return img, biaoqianGray
# DataLoder配合使用代码
# RGB图像及语义分割标签数据绝对路径
trainPath = r"G:\ChanXueYan\dataset\train_val_test\train"
LtrainPath = r"G:\ChanXueYan\dataset\train_val_test\Ltrain"
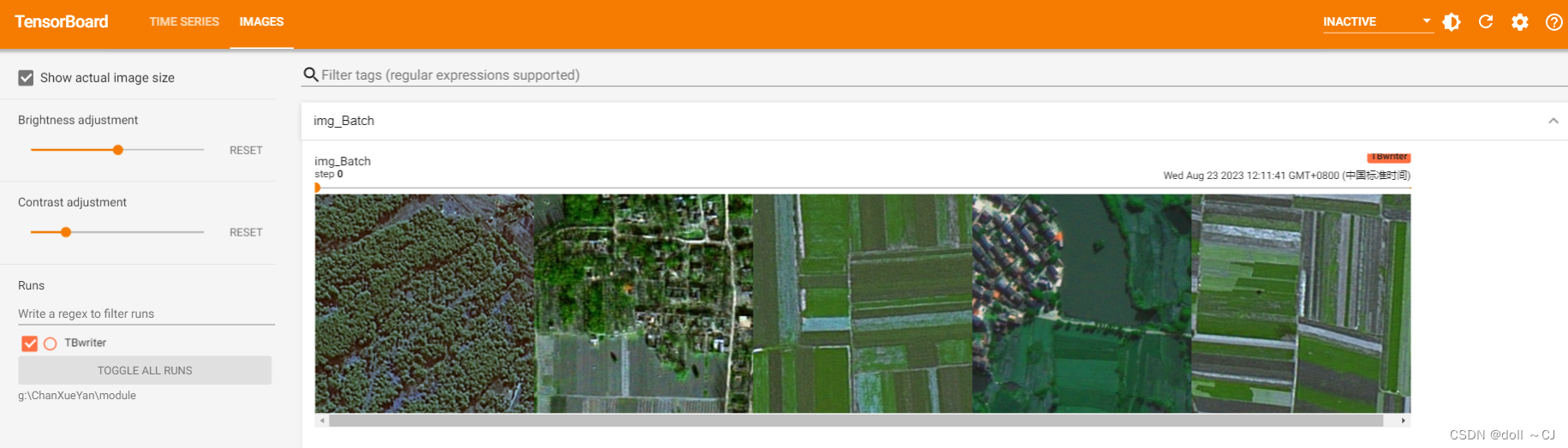
data_train = DataLoader(MyDataset(trainPath, LtrainPath), batch_size=5, shuffle=True, num_workers=0)利用TensorBoard展示读入结果如下:

(二)神经网络模型自定义初始权重实践
具有适合的初始化权重的神经网络通常能获得较好的模型表现。不同的初始化权重方式在不同的激活函数上有不同的表现,例如,通常Kaiming初始化在搭配Relu激活函数后取得较好表现。接下来,我将展示部分Pytorch自定义初始化权重参数的方法。
需要注意的是,如果nn.Sequential容器里嵌套nn.Sequential容器,那么需要另开一个判断容器分支,从而再次在容器里循环初始化。
# 定义两个简单的卷积Block
ConvDemo = nn.Sequential(nn.Conv2d(3,2,3,1,1),nn.BatchNorm2d(2),nn.ReLU(),nn.Conv2d(3,2,3,1,1),nn.BatchNorm2d(2),nn.ReLU())
# 第一种方法
# for layerpart in ConvDemo:
# # isinstance作用为判断变量是否为相同类
# if isinstance(layerpart,nn.Conv2d):
# nn.init.kaiming_normal_(layerpart.weight,mode="fan_out",nonlinearity="relu")
# elif isinstance(layerpart,nn.BatchNorm2d):
# nn.init.constant_(layerpart.weight,1)
# nn.init.constant_(layerpart.bias,0)
# 第二种方法
def init_weights(m):
if type(m) == nn.Conv2d:
nn.init.kaiming_normal_(m.weight,mode="fan_out",nonlinearity="relu")
elif type(m) == nn.BatchNorm2d:
nn.init.constant_(m.weight,1)
nn.init.constant_(m.bias,0)
ConvDemo.apply(init_weights)
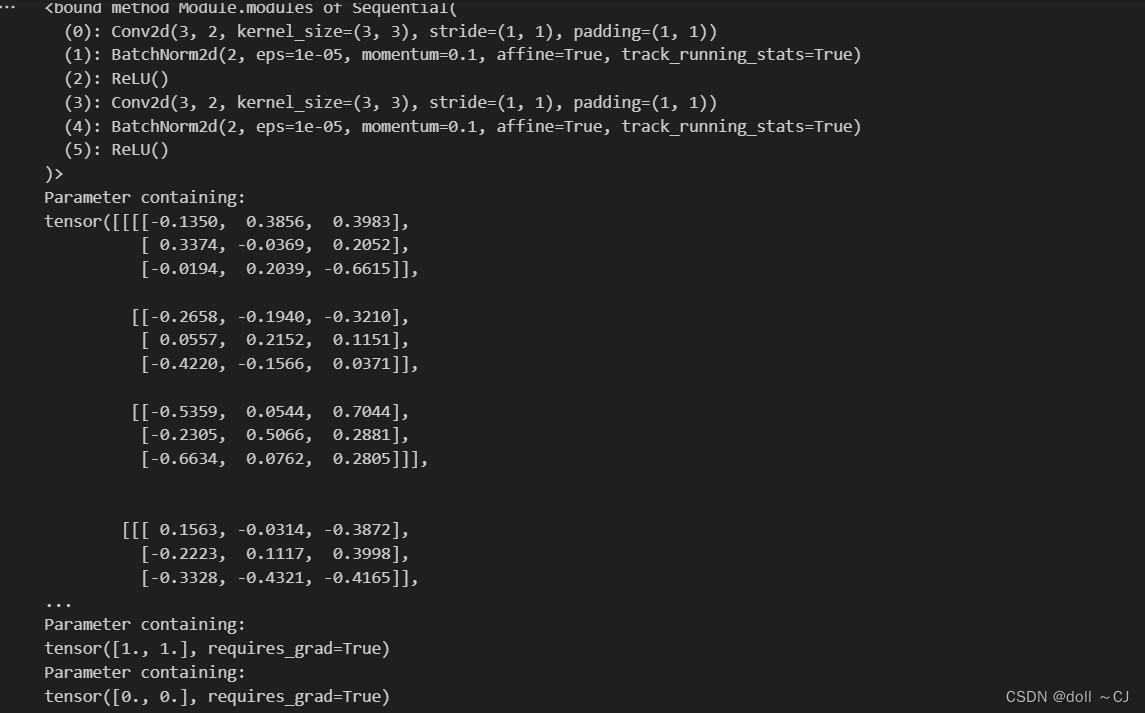
# 查看结果
print(ConvDemo.modules)
# 打印第一层卷积权重
print(ConvDemo[0].weight)
# 打印第一次层批量归一化权重和偏移
print(ConvDemo[1].weight)
print(ConvDemo[1].bias)
结果展示:
(三)神经网络模型自定义学习率下降算法实践
学习率的大小很重要。如果学习率太大,优化会发散;如果太小,训练就会需要过长时间,或者最终只能得到次优的结果。同时,学习率衰减速率同样重要。如果学习率持续过高,我们可能最终会在最小值附近弹跳,从而无法达到最优解。
对于学习率的动态调整,实际上,我们可以在每个迭代轮数(Epoch)或者每个小批量(Step)之后动态调整学习率,从而响应优化。在实现简单的pytorch自定义学习率调整策略时,我们主要定义一个学习率调度器(单因子调度器、多因子调度器)并重写类内__init__()、__call__()和step函数即可。
在pytorch中,我们通常使用以下方式获取并管理模型参数:
object.state_dict()——获取模型中各类对象的参数
current_lr = 优化器实例变量.state_dict()["param_groups"][0]["lr"]——获取当前学习率

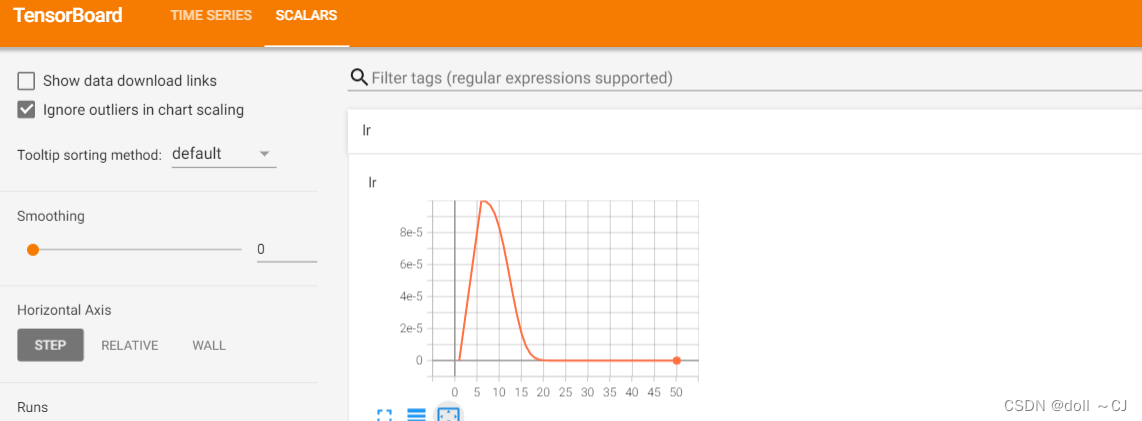
接下来,我以“warmup+余弦调度器”为例,实现学习率自定义动态变化。(补充:余弦调度器是Loshchilov.Hutter.2016提出的一种启发式算法)

# 自定义学习率调度策略
# 该方法未定义scheduler.step()方法,需要在训练过程通过对优化器的学习率参数赋值更新
class WCscheduler:
def __init__(self, base_lr):
self.base_lr = base_lr
# 设置最大cosine余弦下降轮次,在该轮次之后全以final_lr继续训练
self.max_Epoch = 40
# 学习率变化下限(学习率最低值)
# 这里可自己根据实验需求调整(此处仅作随意展示)
self.final_lr = 1e-9
# 预热Epoch数设置,此处可能在5次完全迭代取得较好效果
self.warmup_Epoch = 5
# 预热过程初始学习率(此处仅作随意展示)
self.warmup_begin_lr = 1e-9
# 非预热过程的变化策略迭代总Epoch
self.cosine_Epochs = self.max_Epoch - self.warmup_Epoch
def get_warmup_lr(self, epoch):
warmup_increase = (self.base_lr - self.warmup_begin_lr) * float(epoch) / float( self.warmup_Epoch)
return self.warmup_begin_lr + warmup_increase
def __call__(self, epoch):
if epoch < self.warmup_Epoch:
return self.get_warmup_lr(epoch)
if epoch <= self.max_Epoch:
self.base_lr = self.final_lr + ( self.base_lr - self.final_lr) * (1 + math.cos(math.pi * (epoch - self.warmup_Epoch) / self.cosine_Epochs)) / 2
return self.base_lr
# 学习率调度器(提示作用)
scheduler = WCscheduler(lr)
# 在训练部分加入该部分
# 设置优化器学习率
for param_group in optim.param_groups:
param_group['lr'] = scheduler(epoch)
结果展示:
参考资料:
[1]《动手学深度学习》 — 动手学深度学习 2.0.0 documentation
[2]lr scheduler介绍和可视化 - 知乎
[3]learning rate 的schedule 和callbacks 总结 - 知乎
[4]理解语言的 Transformer 模型 | TensorFlow Core
[5]pytorch之warm-up预热学习策略_pytorch warmup_还能坚持的博客-CSDN博客
[6]源码级理解Pytorch中的Dataset和DataLoader_pytorch dataloader shuffle 所有样本_算法美食屋的博客-CSDN博客
[7]第4章 基础知识进阶 第4.1节 Python基础概念之迭代、可迭代对象、迭代器_LaoYuanPython的博客-CSDN博客
[8]【Python】获取变量占用的内存大小_python查看变量内存大小_是小菜欸的博客-CSDN博客
[9]python中int占几个字节_Python中的整型占多少个字节?_weixin_39997173的博客-CSDN博客
[10]Python彻底搞懂:变量、对象、赋值、引用、拷贝 - 知乎
[11]Xavier初始化_探索世界的小白的博客-CSDN博客
[12]pytorch——计算图与动态图机制_然后就去远行吧的博客-CSDN博客
[13]深度学习相关概念:梯度下降_深度学习梯度下降_AiCharm的博客-CSDN博客
[14]损失函数总结-应用和trick - 知乎
模型表现快速分析和可视化平台(李飞飞老师团队)
Weights & Biases – Developer tools for ML