这里有一幅服务器分布图，服务器的位置标识在 m * n 的整数矩阵网格 grid 中，1 表示单元格上有服务器，0 表示没有。

如果两台服务器位于同一行或者同一列，我们就认为它们之间可以进行通信。

请你统计并返回能够与至少一台其他服务器进行通信的服务器的数量。

示例 1：

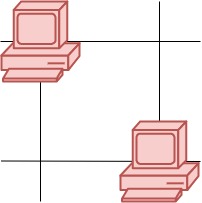
输入：grid = [[1,0],[0,1]]
输出：0
解释：没有一台服务器能与其他服务器进行通信。

示例 2：

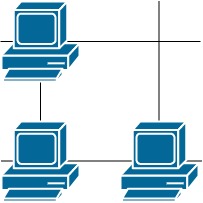
输入：grid = [[1,0],[1,1]]
输出：3
解释：所有这些服务器都至少可以与一台别的服务器进行通信。

示例 3：

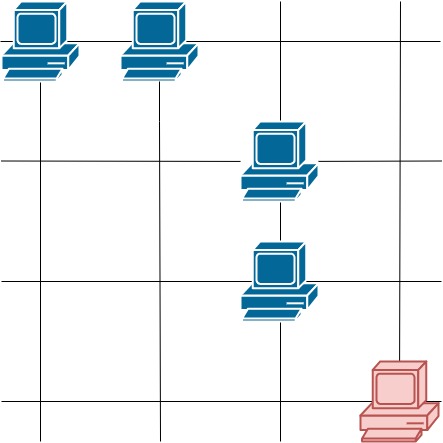
输入：grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]]
输出：4
解释：第一行的两台服务器互相通信，第三列的两台服务器互相通信，但右下角的服务器无法与其他服务器通信。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m <= 250
• 1 <= n <= 250
• grid[i][j] == 0 or 1

思路：

暴力遍历。。。。（我这种肯定不是最优的）

先按行遍历，如果出现第一个，先记录位置，然后看看有没有第二个的出现。

ac code：

class Solution {
    public int countServers(int[][] grid) {
        int ans = 0;
        int n = grid.length;
        int m = grid[0].length;
        boolean[][] vis = new boolean[n][m];
        for (int i = 0;i<n;i++) {
            int flag = 0;
            int firstX = -1;
            int firstY = -1;
            for (int j =0;j<m;j++) {
                if (grid[i][j] == 1) {
                    if (flag > 1) {
                        ans += 1;
                        vis[i][j] = true;
                    } else if (flag == 1) {
                        ans += 2;
                        vis[i][j] = true;
                        vis[firstX][firstY] = true;
                    } else {
                        firstX = i;
                        firstY = j;
                    }
                    flag += 1;
                }
            }
        }

        for (int i=0;i<m;i++) {
            int flag = 0;
            int firstX = -1;
            int firstY = -1;
            for (int j=0;j<n;j++) {
                if (grid[j][i] == 1) {
                    if (flag > 1) {
                        ans += (vis[j][i] ? 0 : 1);
                        vis[j][i] = true;
                    } else if (flag == 1) {
                        ans += (vis[j][i] ? 0 : 1);
                        ans += (vis[firstX][firstY] ? 0 : 1);
                        vis[j][i] = true;
                        vis[firstX][firstY] = true;

                    } else {
                        firstX = j;
                        firstY = i;
                    }
                    flag += 1;
                }
            }
        }
        return ans;
    }
}

还有更优的，比如可以通过hashmap去记录行列是否出现，或者是通过一维数组+一个变量去记录，放一个更优的解法。

class Solution:
    def countServers(self, grid: List[List[int]]) -> int:
        m,n=len(grid),len(grid[0])
        col_alone=[-1]*n
        ans=0
        for i in range(m):
            row_alone=-1
            for j in range(n):
                if grid[i][j]==0:continue
                if row_alone==-1 and col_alone[j]==-1:
                    ##同行同列没有服务器
                    row_alone=j
                    col_alone[j]=i
                else:
                    if row_alone>=0:
                        ans+=1
                        col_alone[row_alone]=-2
                    ans+=(col_alone[j]>=0)+1
                    row_alone=-2
                    col_alone[j]=-2
        return ans