一.定义

 拓扑排序是一种对有向无环图（DAG）进行排序的算法，使得图中的每个顶点在排序中都位于其依赖的顶点之后。它通常用于表示一些任务之间的依赖关系，例如在一个项目中，某些任务必须在其他任务之前完成。

拓扑排序的步骤如下：

1. 找到入度为0的顶点：入度是指指向某个顶点的边的数量。首先，找到图中入度为0的顶点，它们是没有依赖关系的顶点，可以作为排序的起点。

2. 将入度为0的顶点移出图：选择一个入度为0的顶点，将其从图中移除，并将与之相邻的顶点的入度减1。

3. 重复步骤1和步骤2：重复上述步骤，直到所有顶点都被移除。如果图是有向无环图，那么拓扑排序会成功完成。

拓扑排序并不是对所有图都适用，只有在有向无环图中才有意义，因为循环依赖会导致拓扑排序无法进行。

 

---

二.例题

B3644 【模板】拓扑排序 / 家谱树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

三.思路

找出入度为0的点，即为最小辈分的，输出即可，然后取消它的所有连边。

eg：

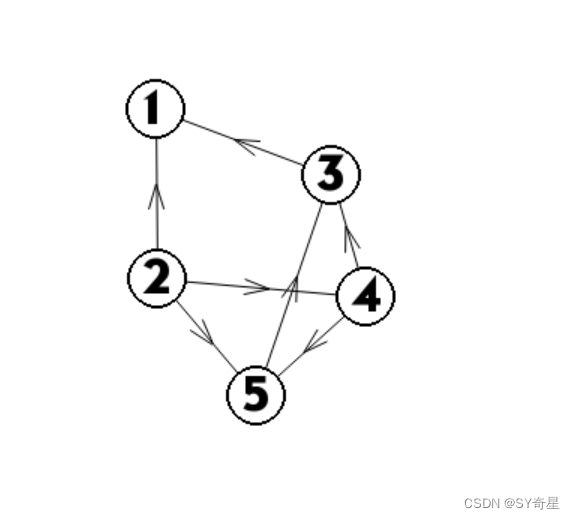
 可知2无入度，说明2的辈分最小，输出并删除它的连边，print(2)

 

这时4无入度,print(2,4)

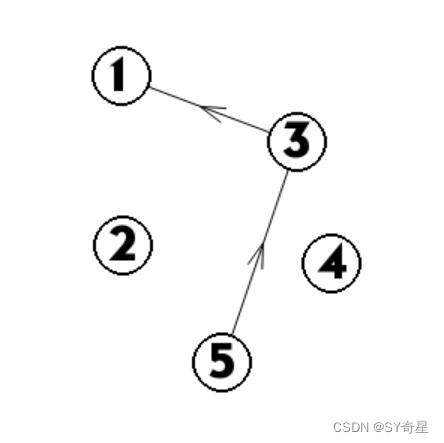
 一直重复，print(2,4,5,3,1)

---

四.参考代码

#include<bits/stdc++.h>
using namespace std;
vector<int>to[101]; 
int in[101];
queue<int>q;
int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		int x;
		while(scanf("%d",&x) && x!=0){
			to[i].push_back(x);
			in[x]++;
		}
	}
	for(int i=1;i<=n;i++){
		if(!in[i]) q.push(i);
	}
	while(!q.empty()){
		int x=q.front();q.pop();
		cout<<x<<" ";
		for(int i=0;i<to[x].size();i++){
			int y=to[x][i];
			in[y]--;
			if(!in[y]) q.push(y);
		}
	}
	return 0;
}

---

五.拓扑+dp

P1807 最长路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

---

六.思路

不就是最长路吗？Dijkstra直接秒杀。

但还有什么更快的算法吗？

注意：这是有向无环图（DAG），是不是拓扑排序更快呢？拓扑排序就可以找到图的所有直径，然后DP即可。最后输出dp[n];

状态转移方程为：dp[v]=max(dp[v],dp[u]+w);

若dp[n]<0，那就说明没有边可以到达n点

---

七.参考代码

#include<bits/stdc++.h>
#define maxn 1505
using namespace std;
int n,m;
vector<int> to[maxn],wt[maxn]; 
int in[maxn],dp[maxn];
queue<int> q;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		to[u].push_back(v);
		wt[u].push_back(w);
		in[v]++; 
	}
	for(int i=1;i<=n;i++){
		dp[i]=-1e9;
		if(in[i]==0) q.push(i) ;
	}
	dp[1]=0;
	while(!q.empty()){
		int x=q.front(); q.pop();
		for(int i=0;i<to[x].size();i++){
			int y=to[x][i],w=wt[x][i];
			dp[y]=max(dp[y],dp[x]+w);
			in[y]--;
			if(!in[y]) q.push(y);
		}
	}
	if(dp[n]<0) cout<<-1;
	else cout<<dp[n];
	return 0;
}