动态不确定性的动态S过程（Matlab代码实现）

news2025/1/10 17:17:22

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

文献来源：

我们展示了如何为建模为线性分数表示并受各种类型的动态不确定性影响的不确定系统组成稳健的稳定性测试。我们的结果是根据线性矩阵不等式制定的，并基于最近建立的有限视界积分二次约束与终端成本的概念。这种约束的构造是由S过程在频域中使用动态拉格朗日乘法器的非常规应用所激发的。我们的技术贡献揭示了如何通过时域中的耗散率参数以无损方式执行这种构造。这为泛化到时变或混合系统开辟了道路。

原文摘要：

We show how to compose robust stability tests for uncertain systems modeled as linear fractional representations and affected by various types of dynamic uncertainties. Our results are formulated in terms of linear matrix inequalities and rest on the recently established notion of finite-horizon integral quadratic constraints with a terminal cost. The construction of such constraints is motivated by an unconventional application of the S-procedure in the frequency domain with dynamic Lagrange multipliers. Our technical contribution reveals how this construction can be performed by dissipativity arguments in the time-domain and in a lossless fashion. This opens the way for generalizations to time-varying or hybrid systems.

📚2 运行结果

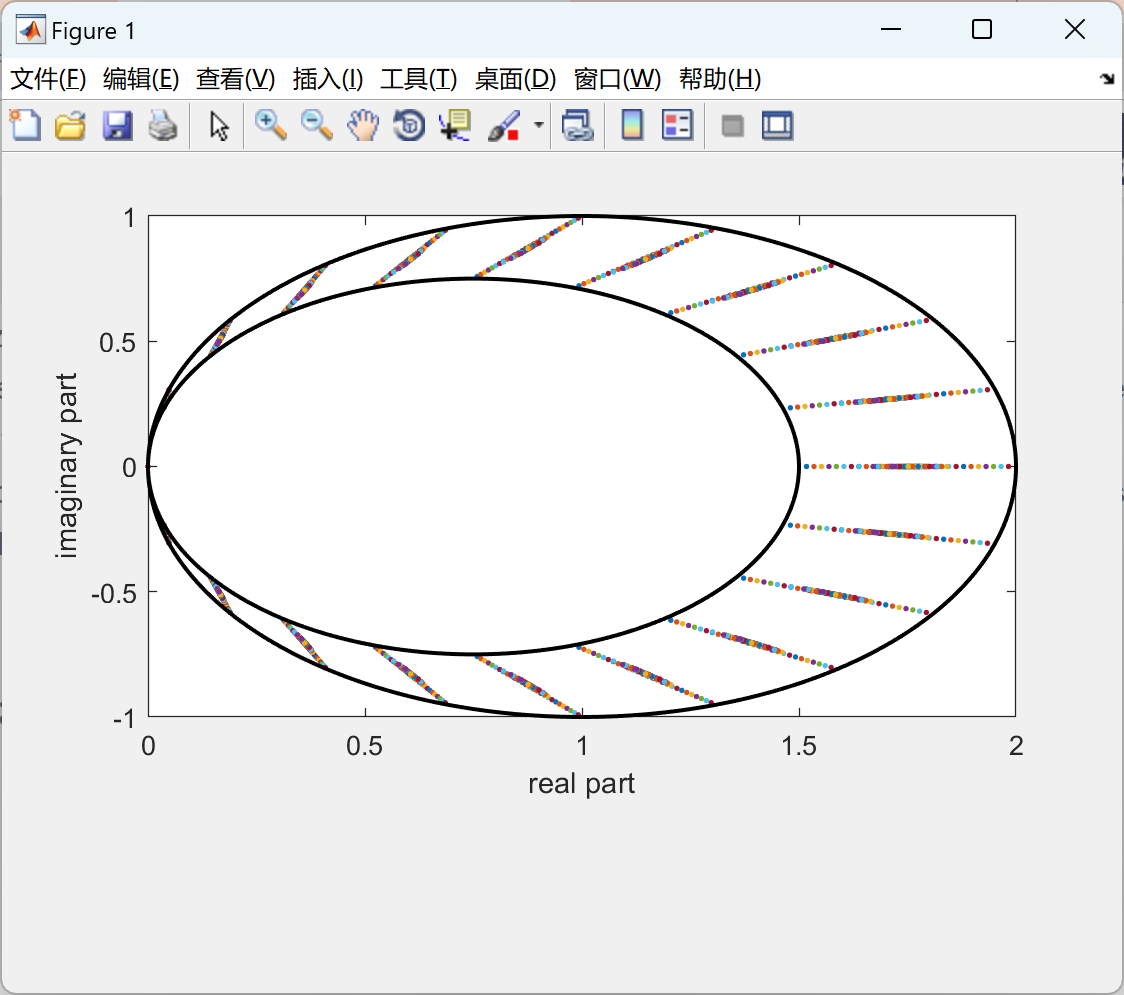
部分代码：

% Involved functions
f1 = @(x) real([1; x(1) + 1i * x(2)]' * [0, 1; 1, -1] * ...
[1; x(1) + 1i * x(2)]); % Outer circle
f2 = @(x) real([1; x(1) + 1i * x(2)]' * [0, -3/4; -3/4, 1] * ...
[1; x(1) + 1i * x(2)]); % Inner circle

% Plotdomain
x = 0:0.01:2;
y = -1:0.01:1;

% Generate grid
[X,Y] = meshgrid(x,y);

% Evaluate functions on grid
Z1 = zeros(length(y), length(x));
Z2 = zeros(length(y), length(x));
for i = 1 : length(y)
for j = 1 : length(x)
Z1(i, j) = f1([x(j); y(i)]);
Z2(i, j) = f2([x(j); y(i)]);
end
end
contour(X,Y,Z1, [0;0], 'linewidth', 1.5, 'color', 'black')
contour(X,Y,Z2, [0;0], 'linewidth', 1.5, 'color', 'black')

xlabel('real part')
ylabel('imaginary part')
%set(gca, 'FontSize', 15)

print('../results/Fig2','-dpng')

%% Gain Bounds

% A very special system, but anyhow
a = -0.1;
% (s + 2 - 1/(del+a)) * (s + del + 1)
sys = ss([(1-3*a)/a, (1-2*a)/a; 1, 0], ...
[-1/a, 0, 1; 0, 0, 0], ...
[a+3+(1-3*a)/a, 1+2*a + (1-2*a)/a; 1, 2; 1, 0], ...
[-1/a, 1, 0; 0, 0, 1; 0, 0, 0]);
% This is constructed in a fashion such that lft(0.5, sys) is unstable

% IO dimensions
p.sys = sys;
p.inp = [2, 1];
p.out = [2, 1];

% Analysis based on covering with single disk. This has to fail since 0.5
% is contained in the disk.
Pi{1} = [0, 1; 1, -1];
ga = ana_rep_intersect(p, Pi);

% More meaningful covering (intersection of interior of a disk and exterior
% of another disk).
Pi{1} = [0, 1; 1, -1];
Pi{2} = [0, -3/4; -3/4, 1];
ga = ana_rep_intersect(p, Pi);
disp(['Gain bound from Theorem 8 with static filter : ', num2str(ga)]);

P = [blkdiag(0, 0), blkdiag(1, -3/4); ...
blkdiag(1, -3/4)', blkdiag(-1, 1)];
ga = ana_rep_region(p, P);
disp(['Gain bound from Theorem 10 with static filter : ', num2str(ga)]);

% Same as above, but with dynamic multipliers
nu = 1;
al = 2;
p.ps = bas(nu, al, p.inp(1));
ga = ana_rep_intersect(p, Pi);
disp(['Gain bound from Theorem 8 with dynamic filter (nu=1): ', ...
num2str(ga)]);