0.卷积操作

深度学习中的卷积操作：https://blog.csdn.net/zyw2002/article/details/128306697

1.注意力

1.1 注意力概述（Attention）

1.1.1 Encoder-Decoder

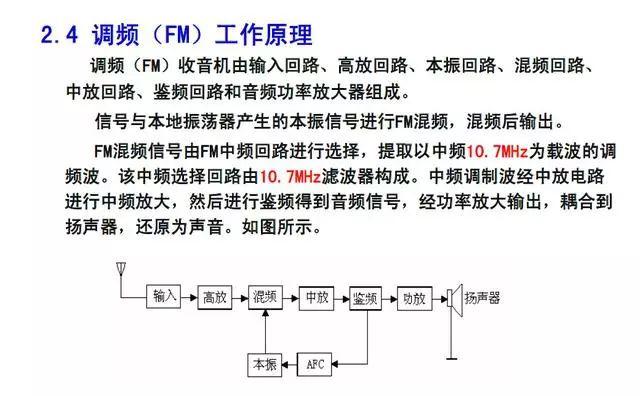
Encoder-Decoder框架顾名思义也就是编码-解码框架，在NLP中Encoder-Decoder框架主要被用来处理序列-序列问题。也就是输入一个序列，生成一个序列的问题。这两个序列可以分别是任意长度。

具体到NLP中的任务比如：

• 文本摘要，输入一篇文章(序列数据)，生成文章的摘要(序列数据)
• 文本翻译，输入一句或一篇英文(序列数据)，生成翻译后的中文(序列数据)
• 问答系统，输入一个question（序列数据），生成一个answer（序列数据）

基于Encoder-Decoder框架具体使用什么模型实现，用的较多的应该就是seq2seq模型和Transformer了。

Encoder-Decoder中的输入和输出

输入
1）输入是一个向量
2）输入是一组向量

输出
1）每一个向量对应一个输出
2）整个序列只输出一个标签

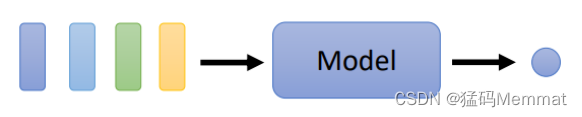
3）模型自己决定输出序列的长度

Encoder-Decoder中的结构原理

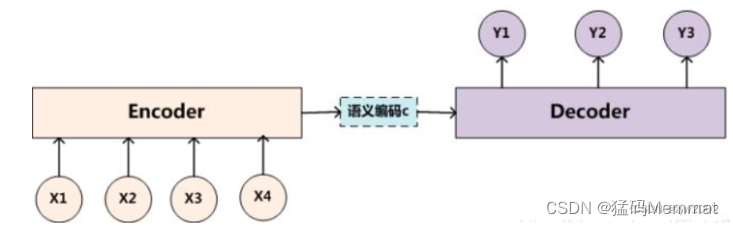
Encoder：编码器，对于输入的序列<x1,x2,x3…xn>进行编码，使其转化为一个语义编码C，这个C中就储存了序列<x1,x2,x3…xn>的信息。

Encoder 是怎么编码的呢？

编码方式有很多种，在文本处理领域主要有RNN/LSTM/GRU/BiRNN/BiLSTM/BiGRU，可以依照自己的喜好来选择编码方式

以RNN为例来具体说明一下：
以上图为例，输入<x1,x2,x3,x4>，通过RNN生成隐藏层的状态值<h1,h2,h3,h4>，如何确定语义编码C呢？最简单的办法直接用最后时刻输出的ht作为C的状态值，这里也就是可以用h4直接作为语义编码C的值，也可以将所有时刻的隐藏层的值进行汇总，然后生成语义编码C的值，这里就是C=q(h1,h2,h3,h4)，q是非线性激活函数。

得到了语义编码C之后，接下来就是要在Decoder中对语义编码C进行解码了。

Decoder：解码器，根据输入的语义编码C，然后将其解码成序列数据，解码方式也可以采用RNN/LSTM/GRU/BiRNN/BiLSTM/BiGRU。

Decoder和Encoder的编码解码方式可以任意组合。

Decoder 是怎么解码的呢？

基于seq2seq模型有两种解码方式：

解码方法1：《Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation》

该方法指出，因为语义编码C包含了整个输入序列的信息，所以在解码的每一步都引入C。文中Ecoder-Decoder均是使用RNN，在计算每一时刻的输出yt时，都应该输入语义编码C，即

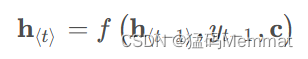
类似的，下一个符号的条件分布是：

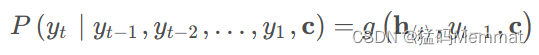
其中$h_t$为当前t时刻的隐藏层的值，$y_{t-1}$为上一时刻的预测输出，作为t时刻的输入，每一时刻的语义编码C是相同地。

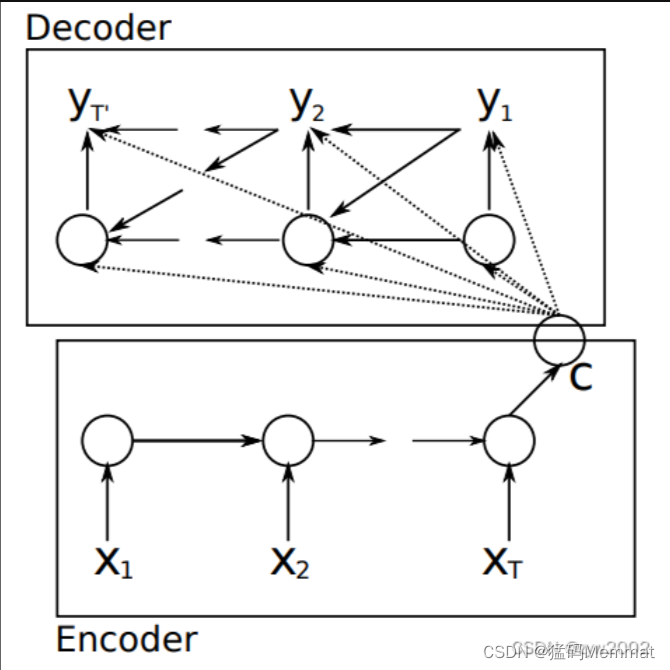
解码方法2：《Sequence to Sequence Learning with Neural Networks》

这个编码方式相对简单，只在Decoder的初始输入引入语义编码C，将语义编码C作为隐藏层状态值$h_0$的初始值，

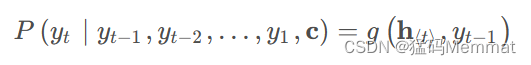
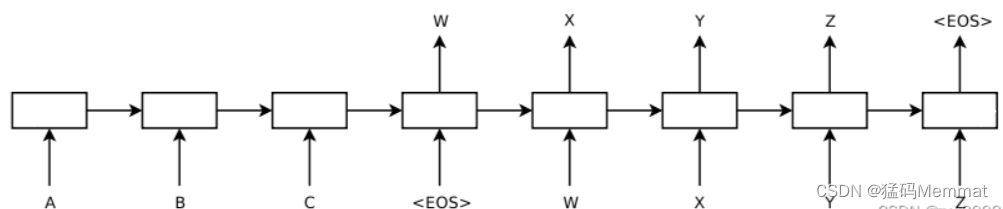
如上图，该模型读取一个输入句子“ABC”，并产生“WXYZ”作为输出句子。模型在输出句尾标记后停止进行预测。注意，LSTM读取反向输入句子，因为这样做会在数据中引入许多短期依赖关系

基于seq2seq模型有两种解码方式都不太好（两种解码方式都只采用了一个语义编码C），而基于attention模型的编码方式中采用了多个C

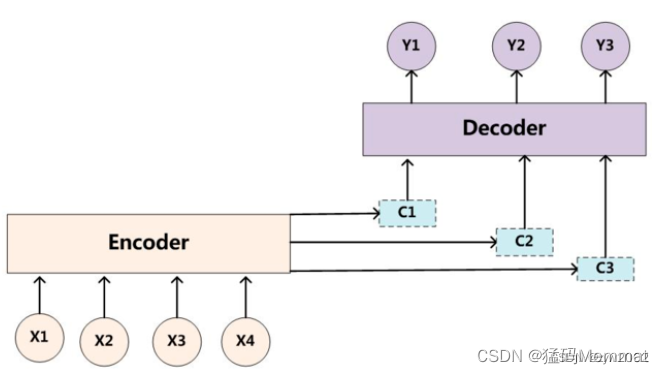
上图就是引入了Attention 机制的Encoder-Decoder框架。咱们一眼就能看出上图不再只有一个单一的语义编码C，而是有多个C1,C2,C3这样的编码。当我们在预测Y1时，可能Y1的注意力是放在C1上，那咱们就用C1作为语义编码，当预测Y2时，Y2的注意力集中在C2上，那咱们就用C2作为语义编码，以此类推，就模拟了人类的注意力机制。

以机器翻译例子"Tom chase Jerry" - "汤姆追逐杰瑞"来说明注意力机制：

当我们在翻译"杰瑞"的时候，为了体现出输入序列中英文单词对于翻译当前中文单词不同的影响程度，比如给出类似下面一个概率分布值：
（Tom,0.3）（Chase,0.2）（Jerry,0.5）

每个英文单词的概率代表了翻译当前单词“杰瑞”时，注意力分配模型分配给不同英文单词的注意力大小。这对于正确翻译目标语单词肯定是有帮助的，因为引入了新的信息。同理，目标句子中的每个单词都应该学会其对应的源语句子中单词的注意力分配概率信息。这意味着在生成每个单词Yi的时候，原先都是相同的中间语义表示C会替换成根据当前生成单词而不断变化的Ci。理解AM模型的关键就是这里，即由固定的中间语义表示C换成了根据当前输出单词来调整成加入注意力模型的变化的Ci。

每个Ci 对应这不同源语句子单词的注意力分配概率，比如对于上面的英汉翻译来说，对应的信息可能如下：

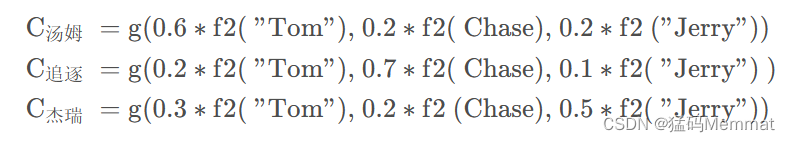
f2(“Tom”),f2(“Chase”),f2(“Jerry”)就是对应的隐藏层的值h(“Tom”),h(“Chase”),h(“Jerry”)。g函数就是加权求和。αi表示权值分布。因此Ci的公式就可以写成：

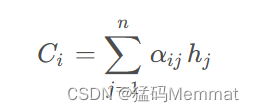
怎么知道attention模型所需要的输入句子单词注意力分配概率分布值$a_{ij}$呢？ 我们可以通过下文介绍的注意力评分函数求得

1.1.2 查询、键和值

下面来看看如何通过自主性的与非自主性的注意力提示， 用神经网络来设计注意力机制的框架。

首先，考虑一个相对简单的状况， 即只使用非自主性提示。 要想将选择偏向于感官输入， 则可以简单地使用参数化的全连接层， 甚至是非参数化的最大汇聚层或平均汇聚层。

在注意力机制的背景下，自主性提示被称为查询（query）。 给定任何查询，注意力机制通过注意力汇聚（attention pooling）将选择引导至感官输入（sensory inputs，例如中间特征表示）。在注意力机制中，这些感官输入被称为值（value）。 更通俗的解释，每个值都与一个键（key）配对， 这可以想象为感官输入的非自主提示。

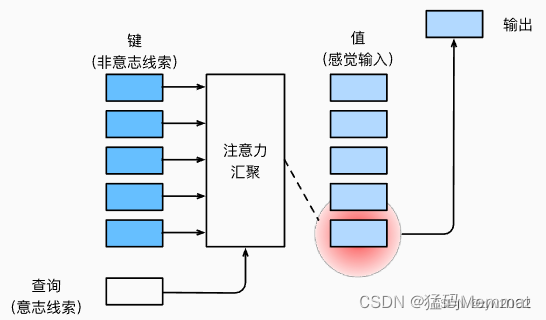
如上图： 注意力机制通过注意力汇聚（注意力的分配方法）将查询（自主性提示）和键（非自主性提示）结合在一起，实现对值（感官输入）的选择倾向。

1.1.3 注意力汇聚： Nadaraya-Watson 核回归

上图中的注意力汇聚是怎么实现的呢？
可通过Nadaraya-Watson核回归模型来了解常见的注意力汇聚模型（平均汇聚、非参数注意力汇聚、带参数注意力汇聚）。

---

为什么要在机器学习中引入注意力机制呢？

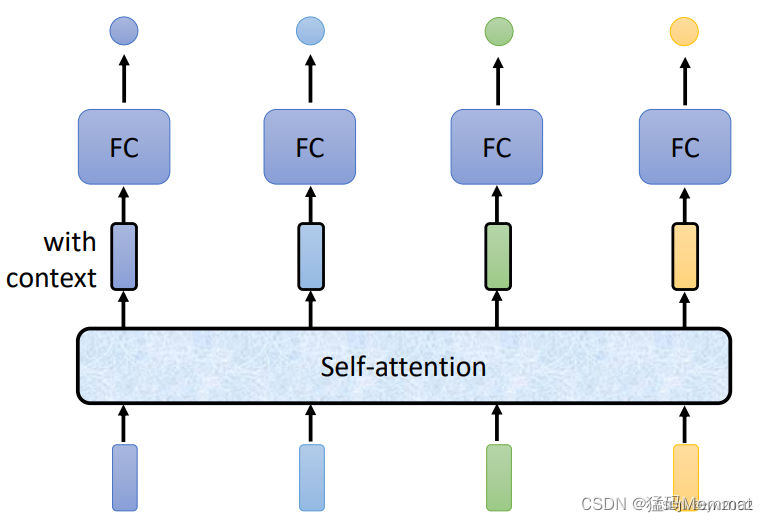
在全连接层，FC只能考虑相邻的几个数据，但是无法考虑到整个序列。

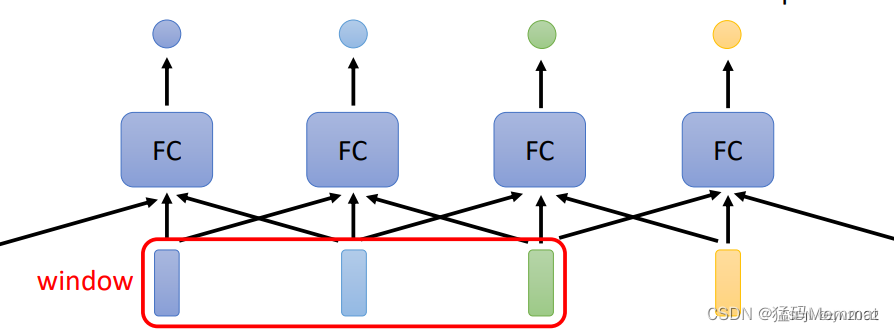
注意力机制（self-attention）可以考虑到整个序列的信息。因此，输出的向量带有全局的上下文信息。

1.2 注意力评分函数

接下来，我们讲解如何通过注意力评分函数来分配注意力。

我们使用高斯核来对查询（query）和键(key)之间的关系建模。 我们可以将高斯核指数部分视为注意力评分函数（attention scoring function）， 简称评分函数（scoring function），然后把这个函数的输出结果输入到softmax函数中进行运算。 通过上述步骤，我们将得到与键对应的值的概率分布（即注意力权重）。最后，注意力汇聚的输出就是基于这些注意力权重的值的加权和。

下图说明了如何将注意力汇聚的输出计算成为值的加权和， 其中a表示注意力评分函数。 由于注意力权重是概率分布， 因此加权和其本质上是加权平均值。


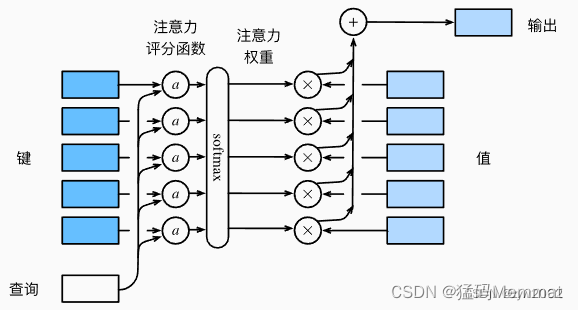
正如我们所看到的，选择不同的注意力评分函数a会导致不同的注意力汇聚操作。 在本节中，我们将介绍两个流行的评分函数(加性注意力、缩放点积注意力)，稍后将用他们来实现更复杂的注意力机制。

---

掩蔽softmax操作

掩蔽softmax操作, 是为实现下文的评分函数做铺垫。

正如上面提到的，softmax操作用于输出一个概率分布作为注意力权重。 在某些情况下，并非所有的值都应该被纳入到注意力汇聚中。 例如，为了高效处理小批量数据集， 某些文本序列被填充了没有意义的特殊词元。 为了仅将有意义的词元作为值来获取注意力汇聚， 我们可以指定一个有效序列长度（即词元的个数）， 以便在计算softmax时过滤掉超出指定范围的位置。 通过这种方式，我们可以在下面的masked_softmax函数中 实现这样的掩蔽softmax操作（masked softmax operation）， 其中任何超出有效长度的位置都被掩蔽并置为0。

#@save
def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
                              value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)

为了演示此函数是如何工作的， 考虑由两个2×4矩阵表示的样本， 这两个样本的有效长度分别为2和3。 经过掩蔽softmax操作，超出有效长度的值都被掩蔽为0。

masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))

tensor([[[0.5423, 0.4577, 0.0000, 0.0000],
         [0.6133, 0.3867, 0.0000, 0.0000]],

        [[0.3324, 0.2348, 0.4329, 0.0000],
         [0.2444, 0.3943, 0.3613, 0.0000]]])

同样，我们也可以使用二维张量，为矩阵样本中的每一行指定有效长度。

masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))

tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
         [0.4142, 0.3582, 0.2275, 0.0000]],

        [[0.5565, 0.4435, 0.0000, 0.0000],
         [0.3305, 0.2070, 0.2827, 0.1798]]])

1.2.1 加性注意力

#@save
class AdditiveAttention(nn.Module):
    """加性注意力"""
    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
        self.w_v = nn.Linear(num_hiddens, 1, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
        queries, keys = self.W_q(queries), self.W_k(keys)
        # 在维度扩展后，
        # queries的形状：(batch_size，查询的个数，1，num_hidden)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # 使用广播方式进行求和
        features = queries.unsqueeze(2) + keys.unsqueeze(1)
        features = torch.tanh(features)
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1)
        self.attention_weights = masked_softmax(scores, valid_lens)
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        return torch.bmm(self.dropout(self.attention_weights), values)

我们用一个小例子来演示上面的AdditiveAttention类， 其中查询、键和值的形状为（批量大小，步数或词元序列长度，特征大小）， 实际输出为(2,1,20)、(2,10,2)和(2,10,4)。 注意力汇聚输出的形状为（批量大小，查询的步数，值的维度）。

queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量，两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(
    2, 1, 1)
valid_lens = torch.tensor([2, 6])

attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,
                              dropout=0.1)
attention.eval()
attention(queries, keys, values, valid_lens)

tensor([[[ 2.0000,  3.0000,  4.0000,  5.0000]],

        [[10.0000, 11.0000, 12.0000, 13.0000]]], grad_fn=<BmmBackward0>)

尽管加性注意力包含了可学习的参数，但由于本例子中每个键都是相同的， 所以注意力权重是均匀的，由指定的有效长度决定。

d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')

1.2.2 缩放点积注意力

在下面的缩放点积注意力的实现中, 我们使用了暂退法进行模型正则化。

#@save
class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)

为了演示上述的DotProductAttention类， 我们使用与先前加性注意力例子中相同的键、值和有效长度。 对于点积操作，我们令查询的特征维度与键的特征维度大小相同。

queries = torch.normal(0, 1, (2, 1, 2))
attention = DotProductAttention(dropout=0.5)
attention.eval()
attention(queries, keys, values, valid_lens)

tensor([[[ 2.0000,  3.0000,  4.0000,  5.0000]],
        [[10.0000, 11.0000, 12.0000, 13.0000]]])

与加性注意力演示相同，由于键包含的是相同的元素， 而这些元素无法通过任何查询进行区分，因此获得了均匀的注意力权重。

d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')

1.3 自注意力（Self-Attention）

1.3.1 自注意力的定义和计算

首先我们先来看看Attention的优缺点。

• Attention 的优点：

1. 速度快。Attention机制不再依赖于RNN，解决了RNN不能并行计算的问题。这里需要说明一下，基于Attention机制的seq2seq模型，因为是有监督的训练，所以咱们在训练的时候，在decoder阶段并不是说预测出了一个词，然后再把这个词作为下一个输入，因为有监督训练，咱们已经有了target的数据，所以是可以并行输入的，可以并行计算decoder的每一个输出，但是再做预测的时候，是没有target数据地，这个时候就需要基于上一个时间节点的预测值来当做下一个时间节点decoder的输入。所以节省的是训练的时间。
2. 效果好。效果好主要就是因为注意力机制，能够获取到局部的重要信息，能够抓住重点。

• Attention 的缺点

1. 只能在Decoder阶段实现并行运算，Encoder部分依旧采用的是RNN，LSTM这些按照顺序编码的模型，Encoder部分还是无法实现并行运算，不够完美。
2. 就是因为Encoder部分目前仍旧依赖于RNN，所以对于中长距离之间，两个词相互之间的关系没有办法很好的获取。

Self-Attention 是在Attention的基础上，针对上述的两个缺点进行改进得到的。

• Self-Attention和Attention的区别
  在一般任务的Encoder-Decoder框架中，输入Source和输出Target内容是不一样的。比如对于英-中机器翻译来说，Source是英文句子，Target是对应的翻译出的中文句子，Attention机制发生在Target的元素和Source中的所有元素之间。
  Self Attention，指的是Source内部元素之间或者Target内部元素之间发生的Attention机制，也可以理解为Target=Source这种特殊情况下的注意力计算机制

1.3.2 自注意力的应用

自然语言处理
Self-Attention最广泛的应用是在自然语言处理（Natural Langue Processing ，NLP）

• Transformer《Attention Is All You Need》
• BERT 《BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding》

语音处理

• Truncated Self-Attention 《Transformer-Transducer: End-to-End Speech Recognition with Self-Attention》

以往的attention是注意在整个sequence上面，而truncated self-attention只考虑部分sequence，因为语音的sequence非常长。具体多长是一个需要调整的参数，也就是说只注意一个窗口内的元素，至于这个窗口是多大是一个待调整的参数。

图像处理

一张图片也可以看做是一组向量

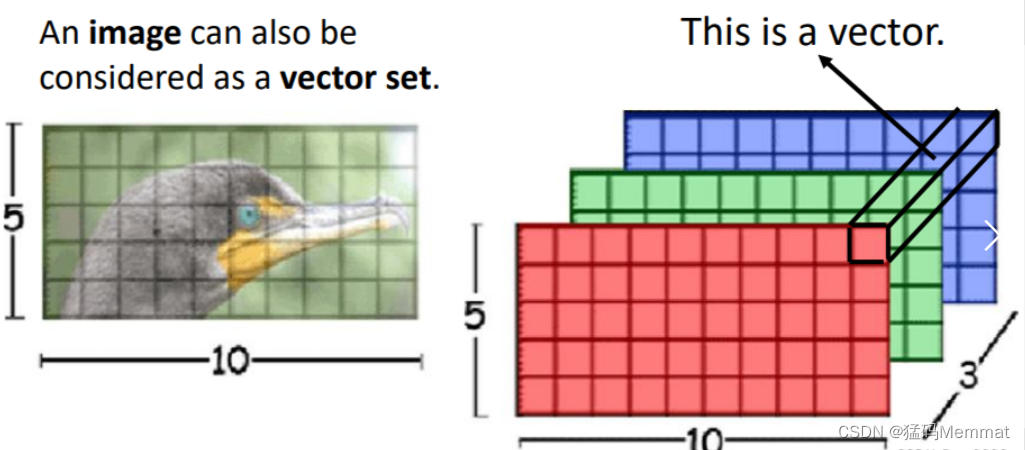
• Self-Attention GAN 《Self-Attention Generative Adversarial Networks》:https://arxiv.org/abs/2005.12872
  
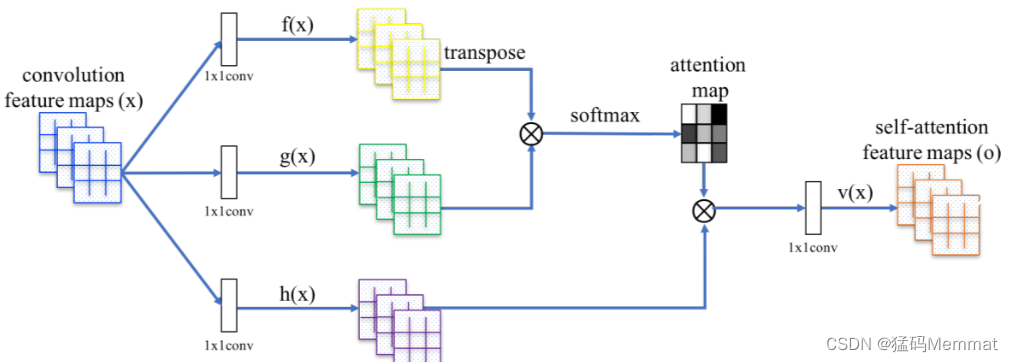
• Detection Transformer (DETR) 《End-to-End Object Detection with Transformers》:https://arxiv.org/abs/2005.12872

1.3.3 Self-Attention 与 CNN 与 RNN

下面我们来看一下Self-Attention 和 卷积神经网络（CNN）、循环神经网络（RNN）之间的区别和联系。

---

Self-attention 🆚 CNN

CNN只能注意到recptive filed中的内容，可以把CNN看做一个简化的Self-attention。
也可以把Self-attention看做是具有learnable receptive field 的CNN.

《On the Relationship between Self-Attention and Convolutional Layers》 介绍了Self-Attention和CNN之间的关系

《An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale》 表明：在少量数据的情况下，CNN表现的更好。但是在大量的数据下，Self-Attention的表现更出色。

---

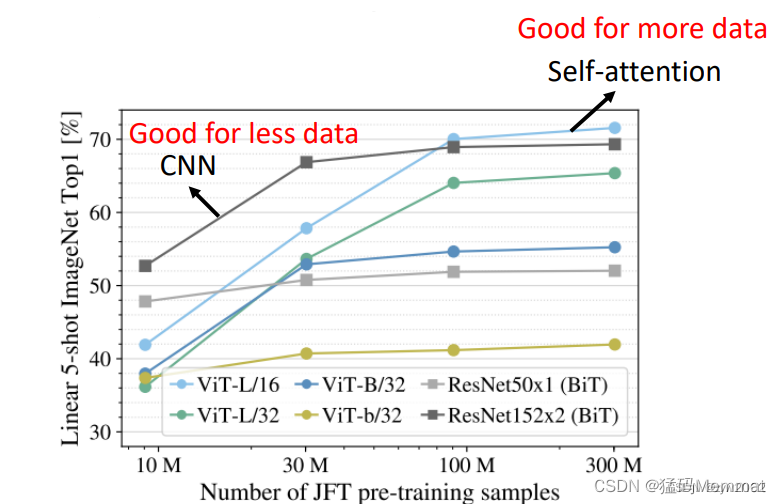
Self-attention 🆚 RNN
1）对于RNN而言，在序列开始的的元素，随着序列的增加，很难影响到靠后的元素；而对于Self-Attention而言，考虑了全局的注意力信息，序列中靠前的元素依然可能对靠后的元素产生较大的影响。
2）对于RNN而言，当前时间点元素的输出都依赖于前一个时间点元素的输出。是顺序操作的，无法并行；而对于Self-Attention而言，是可以并行操作的，提升了计算效率。

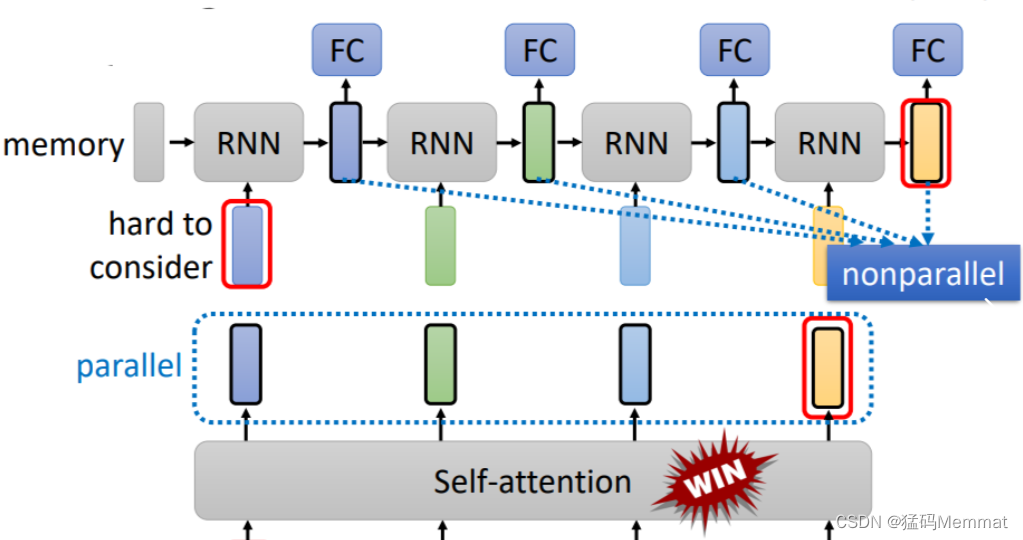
《Transformers are RNNs:Fast Autoregressive Transformers with Linear Attention》 这篇文章进一步介绍了Transformer和RNN之间的关系

---

Self-Attention 🆚 CNN 🆚 RNN
接下来比较下面几个架构，目标都是将由n个词元组成的序列映射到另一个长度相等的序列，其中的每个输入词元或输出词元都由d维向量表示。具体来说，将比较的是卷积神经网络、循环神经网络和自注意力这几个架构的计算复杂性、顺序操作和最大路径长度。请注意，顺序操作会妨碍并行计算，而任意的序列位置组合之间的路径越短，则能更轻松地学习序列中的远距离依赖关系


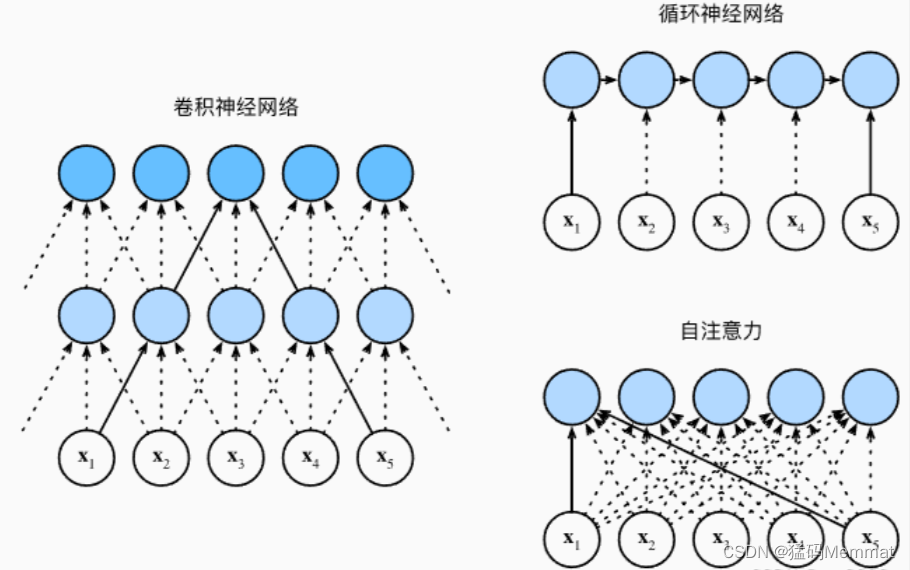
总而言之，卷积神经网络和自注意力都拥有并行计算的优势， 而且自注意力的最大路径长度最短。 但是因为其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢。

1.4 多头自注意力 (Multihead Attention)

在实践中，当给定相同的查询、键和值的集合时， 我们希望模型可以基于相同的注意力机制学习到不同的行为， 然后将不同的行为作为知识组合起来， 捕获序列内各种范围的依赖关系 （例如，短距离依赖和长距离依赖关系）。 因此，允许注意力机制组合使用查询、键和值的不同子空间表示（representation subspaces）可能是有益的。

#@save
class MultiHeadAttention(nn.Module):
    """多头注意力"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = d2l.DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)

    def forward(self, queries, keys, values, valid_lens):
        # queries，keys，values的形状:
        # (batch_size，查询或者“键－值”对的个数，num_hiddens)
        # valid_lens　的形状:
        # (batch_size，)或(batch_size，查询的个数)
        # 经过变换后，输出的queries，keys，values　的形状:
        # (batch_size*num_heads，查询或者“键－值”对的个数，
        # num_hiddens/num_heads)
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)

        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)

        # output的形状:(batch_size*num_heads，查询的个数，
        # num_hiddens/num_heads)
        output = self.attention(queries, keys, values, valid_lens)

        # output_concat的形状:(batch_size，查询的个数，num_hiddens)
        output_concat = transpose_output(output, self.num_heads)
        return self.W_o(output_concat)

为了能够使多个头并行计算， 上面的MultiHeadAttention类将使用下面定义的两个转置函数。 具体来说，transpose_output函数反转了transpose_qkv函数的操作。

#@save
def transpose_qkv(X, num_heads):
    """为了多注意力头的并行计算而变换形状"""
    # 输入X的形状:(batch_size，查询或者“键－值”对的个数，num_hiddens)
    # 输出X的形状:(batch_size，查询或者“键－值”对的个数，num_heads，
    # num_hiddens/num_heads)
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)

    # 输出X的形状:(batch_size，num_heads，查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    X = X.permute(0, 2, 1, 3)

    # 最终输出的形状:(batch_size*num_heads,查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    return X.reshape(-1, X.shape[2], X.shape[3])

#@save
def transpose_output(X, num_heads):
    """逆转transpose_qkv函数的操作"""
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    X = X.permute(0, 2, 1, 3)
    return X.reshape(X.shape[0], X.shape[1], -1)

下面我们使用键和值相同的小例子来测试我们编写的MultiHeadAttention类。 多头注意力输出的形状是（batch_size，num_queries，num_hiddens）。

num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
                               num_hiddens, num_heads, 0.5)
attention.eval()

MultiHeadAttention(
  (attention): DotProductAttention(
    (dropout): Dropout(p=0.5, inplace=False)
  )
  (W_q): Linear(in_features=100, out_features=100, bias=False)
  (W_k): Linear(in_features=100, out_features=100, bias=False)
  (W_v): Linear(in_features=100, out_features=100, bias=False)
  (W_o): Linear(in_features=100, out_features=100, bias=False)
)

batch_size, num_queries = 2, 4
num_kvpairs, valid_lens =  6, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))
attention(X, Y, Y, valid_lens).shape
# torch.Size([2, 4, 100])

2. Transformer

论文《Attention is all you need》 是Transformer模型的开山之作

Transformer 的整体结构主要由三部分组成：Input 、Encoder-Decoder 、Output

可见之前文章：略

2.1 Transformer的整体结构

略

2.2 Transformer的输入

Transformer 中单词的输入表示 x由Input Embeddings(单词向量)和Poditional Encoding(位置编码)相加得到。

2.2.1 单词Embedding

单词的 Embedding 有很多种方式可以获取，例如可以采用 Word2Vec、Glove， one-hot 等算法预训练得到，也可以在 Transformer 中训练得到。

2.2.2 位置Encoding

Transformer 中除了单词的 Embedding，还需要使用位置Embedding 表示单词出现在句子中的位置。因为 Transformer 不采用 RNN 的结构，而是使用全局信息，不能利用单词的顺序信息，而这部分信息对于 NLP 来说非常重要。所以 Transformer 中使用位置 Embedding 保存单词在序列中的相对或绝对位置。

在处理词元序列时，循环神经网络是逐个的重复地处理词元的， 而自注意力则因为并行计算而放弃了顺序操作。
为了使用序列的顺序信息，通过在输入表示中添加位置编码（positional encoding）来注入绝对的或相对的位置信息。
位置编码可以通过学习得到也可以直接固定得到。

Transformer中采用的是基于正弦函数和余弦函数的固定位置编码；BERT中的位置编码是通过训练得到的。

---

基于正弦函数和余弦函数的固定位置编码

《Attention Is All You Need》论文中Transformer使用的是正余弦位置编码。位置编码通过使用不同频率的正弦、余弦函数生成，然后和对应的位置的词向量相加，位置向量维度必须和词向量的维度一致。

#@save
class PositionalEncoding(nn.Module):
    """位置编码"""
    def __init__(self, num_hiddens, dropout, max_len=1000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros((1, max_len, num_hiddens))
        X = torch.arange(max_len, dtype=torch.float32).reshape(
            -1, 1) / torch.pow(10000, torch.arange(
            0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)

---

绝对位置信息
为了明白沿着编码维度单调降低的频率与绝对位置信息的关系， 让我们打印出0,1,…,7的二进制表示形式。 正如所看到的，每个数字、每两个数字和每四个数字上的比特值 在第一个最低位、第二个最低位和第三个最低位上分别交替。

for i in range(8):
    print(f'{i}的二进制是：{i:>03b}')

0的二进制是：000
1的二进制是：001
2的二进制是：010
3的二进制是：011
4的二进制是：100
5的二进制是：101
6的二进制是：110
7的二进制是：111

2.3 Transformer的Encoder-Decoder

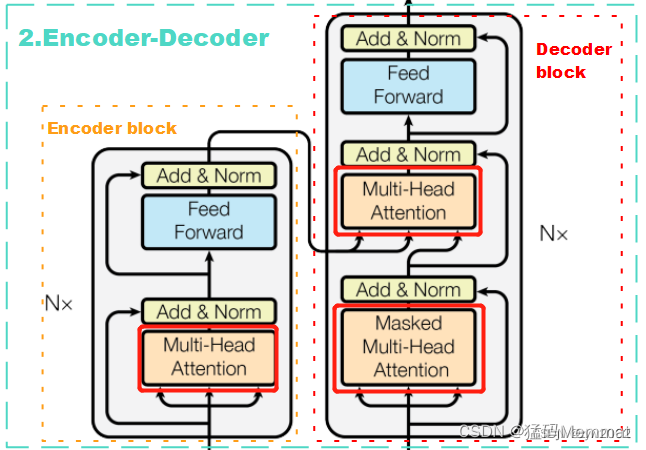
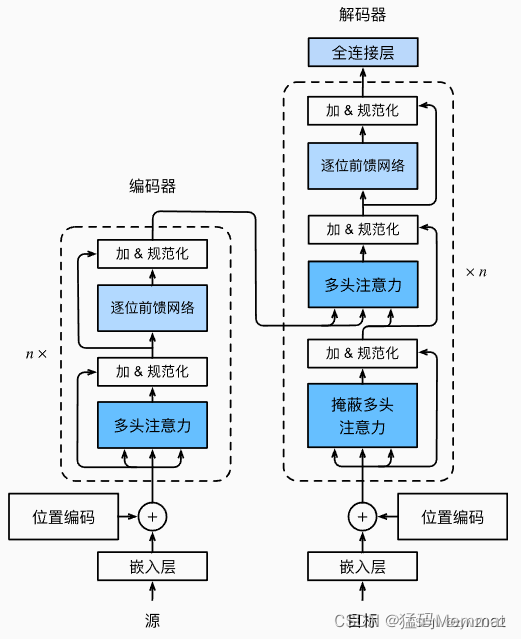
论文中 Transformer 的内部结构图，左侧为 Encoder block，右侧为 Decoder block。红色圈中的部分为 Multi-Head Attention，是由多个 Self-Attention组成的，可以看到 Encoder block 包含一个 Multi-Head Attention，而 Decoder block 包含两个 Multi-Head Attention (其中有一个用到 Masked)。Multi-Head Attention 上方还包括一个 Add & Norm 层，Add 表示残差连接 (Residual Connection) 用于防止网络退化，Norm 表示 Layer Normalization，用于对每一层的激活值进行归一化。

2.3.1 Encoder block

Encoder block 中包括N个Encoder, 每个Encoder的结构相同，但是权重不共享。
每个Encoder主要由Multi-Head Attention、Add&Norm、Feed Forward 三种结构。接下来，我们将依次讲解这三种结构。

---

Multi-Head Attention

---

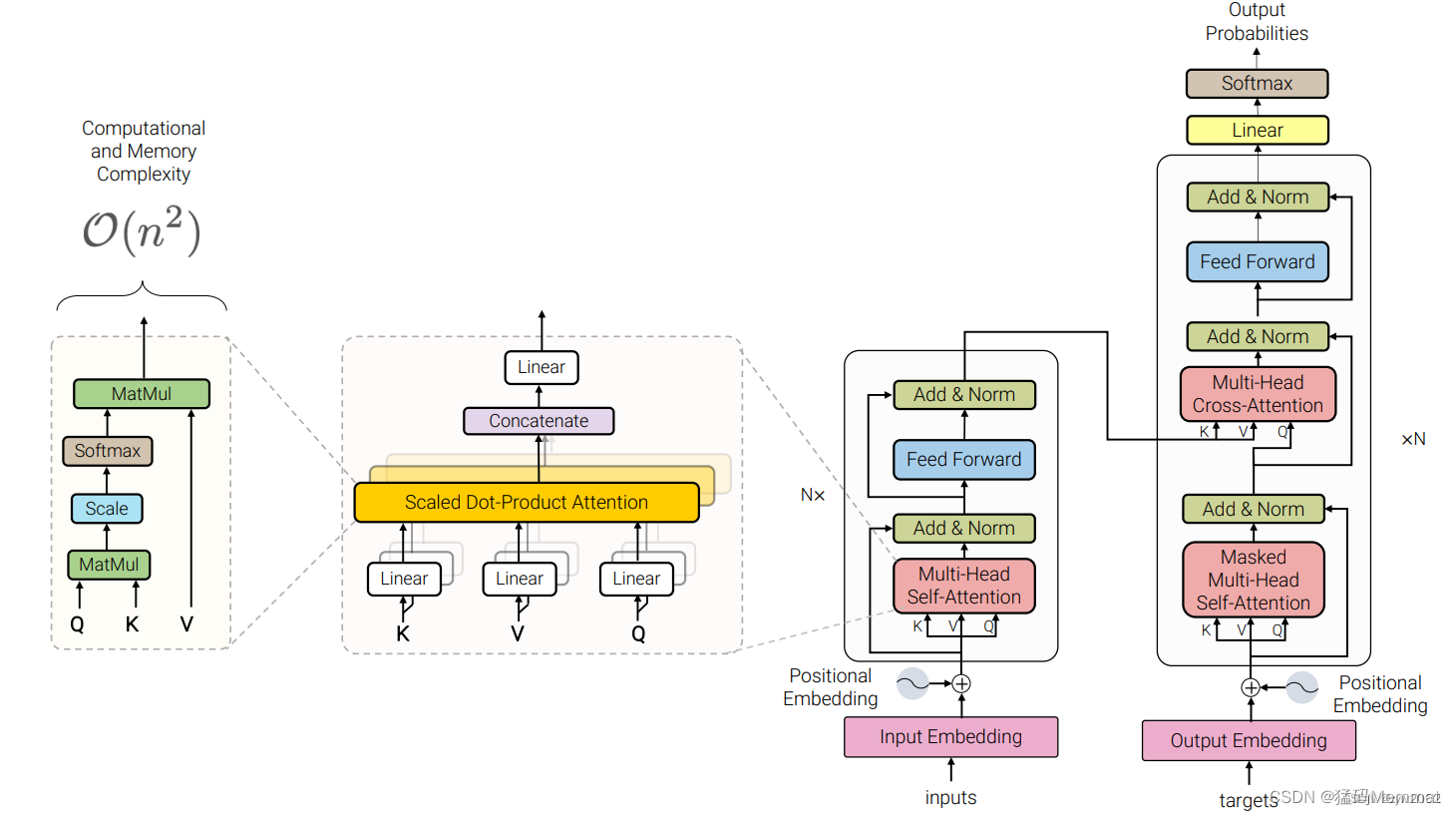
Add＆Normalize

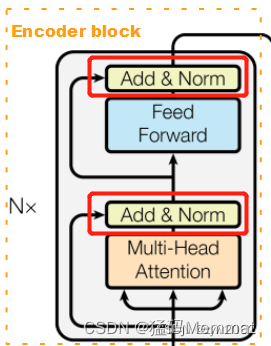
每个编码器中的每个子层（自注意力层、前馈神经网络）都有一个残差连接(Add)，之后是做了一个层归一化（layer-normalization）。

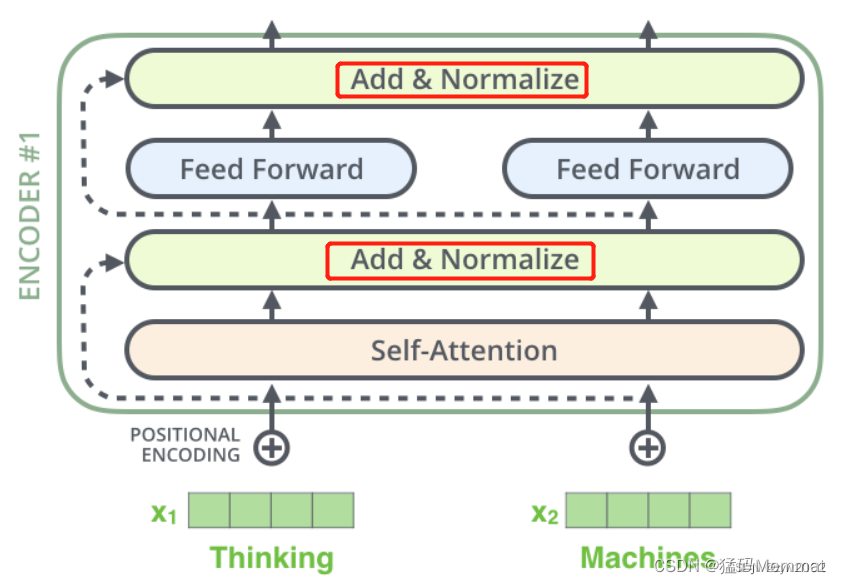
将过程中的向量相加和layer-norm可视化如下所示：

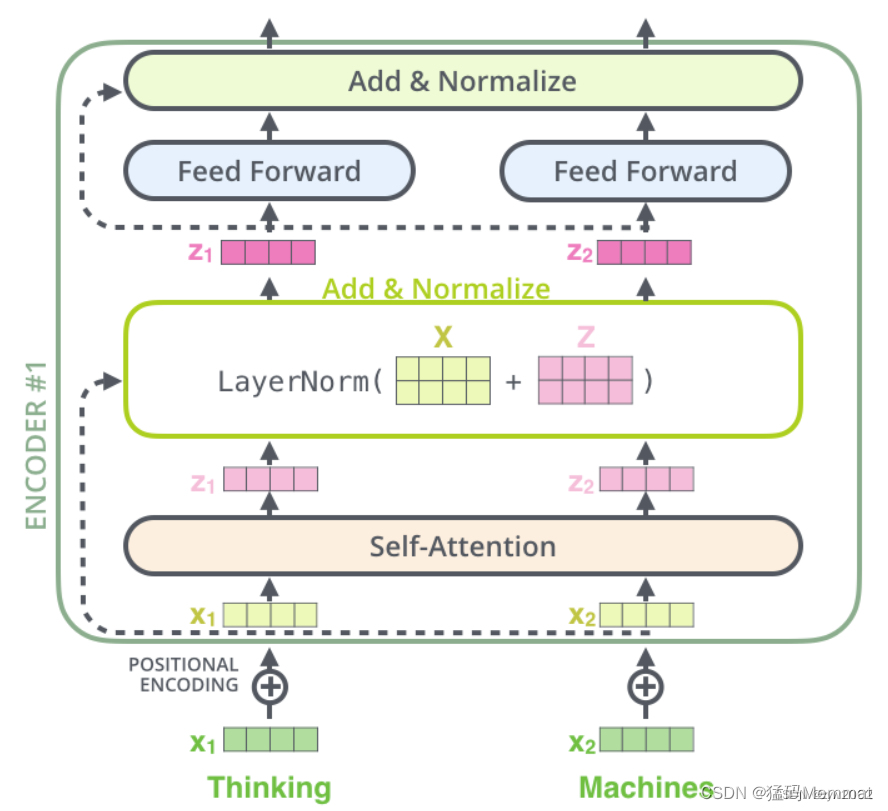
• Add
  Add，就是在Z的基础上加了一个残差块X，加入残差块X的目的是为了防止在深度神经网络训练中发生退化问题。
  退化的意思就是深度神经网络通过增加网络的层数，Loss逐渐减小，然后趋于稳定达到饱和，然后再继续增加网络层数，Loss反而增大。

为什么深度神经网络会发生退化?

举个例子：假如某个神经网络的最优网络层数是18层，但是我们在设计的时候并不知道到底多少层是最优解，本着层数越深越好的理念，我们设计了32层，那么32层神经网络中有14层其实是多余地，我们要想达到18层神经网络的最优效果，必须保证这多出来的14层网络必须进行恒等映射，恒等映射的意思就是说，输入什么，输出就是什么，可以理解成F(x)=x这样的函数，因为只有进行了这样的恒等映射咱们才能保证这多出来的14层神经网络不会影响我们最优的效果。

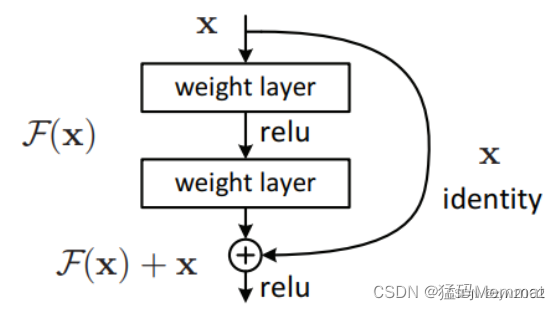
残差块又是什么？

上图就是构造的一个残差块，可以看到X是这一层残差块的输入，也称作F(X)为残差，X为输入值，F(X)是经过第一层线性变化并激活后的输出，该图表示在残差网络中，第二层进行线性变化之后激活之前，F(X)加入了这一层输入值X，然后再进行激活后输出。在第二层输出值激活前加入X，这条路径称作shortcut连接。

为什么添加了残差块能防止神经网络退化问题呢？

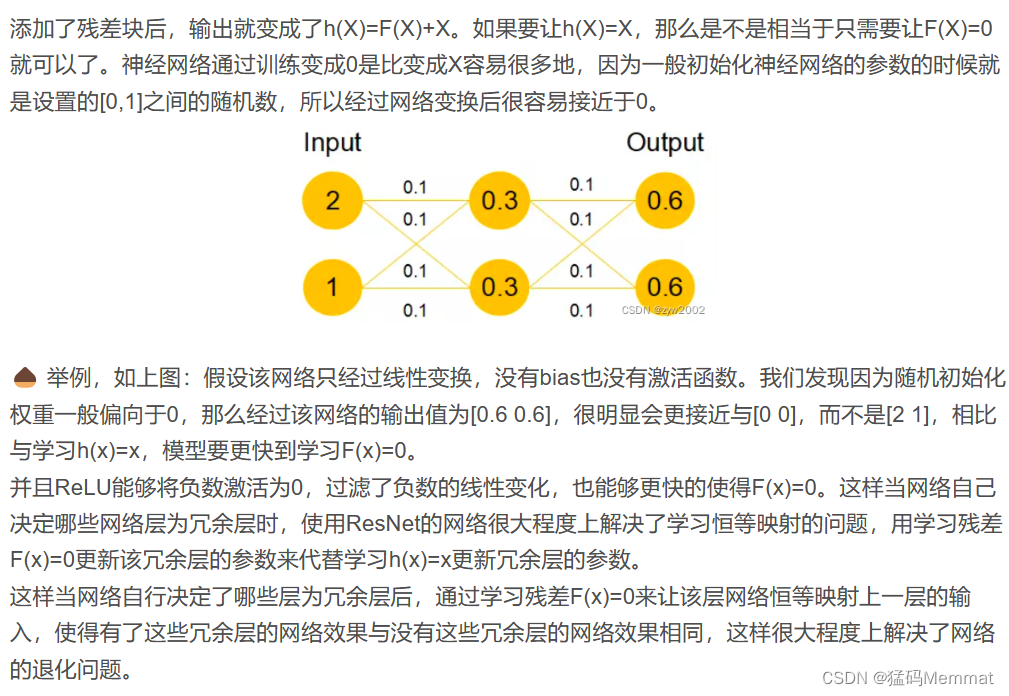
Transformer中加上的X也就是Multi-Head Attention的输入，X矩阵。

为什么要进行Normalize呢？

在神经网络进行训练之前，都需要对于输入数据进行Normalize归一化，目的有二：1，能够加快训练的速度。2.提高训练的稳定性。

什么是Layer Normalization，什么是Batch Normalization

《Layer Normalization》 首次提出了层规范化。
《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》 首次提出了批量规范化
Batch Normalization 的处理对象是对一批样本， Layer Normalization 的处理对象是单个样本。Batch Normalization 是对这批样本的同一维度特征做归一化， Layer Normalization 是对这单个样本的所有维度特征做归一化。

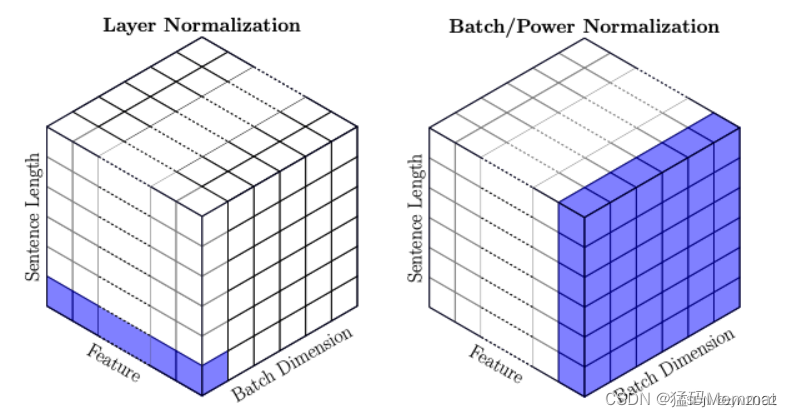
为什么使用Layer Normalization（LN）而不使用Batch Normalization（BN）呢？

1. 论文《PowerNorm: Rethinking Batch Normalization in Transformers》指出，Transformer中BN表现不太好的原因可能在于CV和NLP数据特性的不同，对于NLP数据，前向和反向传播中，batch统计量及其梯度都不太稳定。

2. 论文《Understanding and Improving Layer Normalization》主要研究LN的优点，除了一般意义上认为可以稳定前向输入分布，加快收敛快，还有没有啥原因。最后的结论有：
   a）相比于稳定前向输入分布，反向传播时mean和variance计算引入的梯度更有用，可以稳定反向传播的梯度
   b) 去掉 gain和bias这两个参数可以在很多数据集上有提升，可能是因为这两个参数会带来过拟合，因为这两个参数是在训练集上学出来的

3. 论文《Leveraging Batch Normalization for Vision Transformers》研究对于CV data，能不能使用BN。主要提出了如下观点：
   1）LN特别适合处理变长数据，因为是对channel维度做操作(这里指NLP中的hidden维度)，和句子长度和batch大小无关
   2）BN比LN在inference的时候快，因为不需要计算mean和variance，直接用running mean和running variance就行
   3）直接把VIT中的LN替换成BN，容易训练不收敛，原因是FFN没有被Normalized，所以还要在FFN block里面的两层之间插一个BN层。（可以加速20% VIT的训练）

Layer Normalization 的位置可以改变吗？

论文《On Layer Normalization in the Transformer Architecture》研究了为什么学习率预热阶段在训练Transformer中很重要，并表明层归一化的位置很重要。原始的Transformer，LN位于残差块之外(如下图a)，在初始化时输出层附近参数的期望梯度很大。当使用大的学习率时，这会导致训练的不稳定；在残差块中使用LN的Transformer(如下图b)，可以在没有预热阶段的情况下进行训练，并且收敛得更快。

---

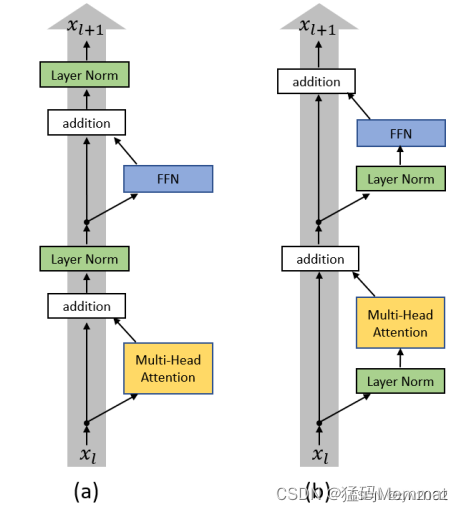
Feed-Forward Networks

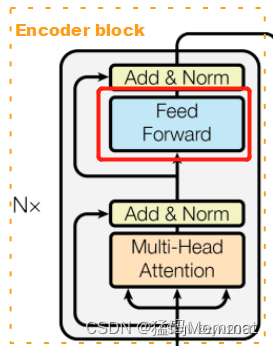
全连接层公式如下：

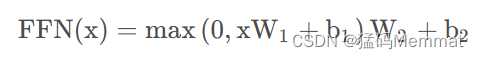
这里的全连接层是一个两层的神经网络，先线性变换，然后ReLU非线性，再线性变换。
这里的x就是我们Multi-Head Attention的输出Z，还是引用上面的例子，那么Z是(2,512)维的矩阵，假设W1是(512,1024)，其中W2与W1维度相反(1024,612)，那么按照上面的公式：FFN(Z)=(2,512)x(512,1024)x(1024,512)=(2,512)，我们发现维度没有发生变化，这两层网络就是为了将输入的Z映射到更加高维的空间中(2,64)x(64,1024)=(2,1024)，然后通过非线性函数ReLU进行筛选，筛选完后再变回原来的维度。

然后经过Add＆Normalize，输入下一个encoder中，经过6个encoder后输入到decoder中，至此Transformer的Encoder部分就全部介绍完了。

2.3.2 Decoder block

解码器有两种类型，自回归的Decoder（AT）和非自回归的解码器（NAT

2.4 Transformer的输出

Decoder输出的是一个浮点型向量，如何把它变成一个词？这就是最后一个线性层和softmax要做的事情。

2.5 Transformer的训练过程和损失函数

2.5.1 训练过程

2.5.2 损失函数

2.6 Transformer的代码实现

首先，先导入需要的包

import math
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l

2.6.1 基于位置的前馈神经网络

基于位置的前馈网络对序列中的所有位置的表示进行变换时使用的是同一个多层感知机（MLP），这就是称前馈网络是基于位置的（positionwise）的原因。在下面的实现中，输入X的形状（批量大小，时间步数或序列长度，隐单元数或特征维度）将被一个两层的感知机转换成形状为（批量大小，时间步数，ffn_num_outputs）的输出张量。

#@save
class PositionWiseFFN(nn.Module):
    """基于位置的前馈网络"""
    def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs,
                 **kwargs):
        super(PositionWiseFFN, self).__init__(**kwargs)
        self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
        self.relu = nn.ReLU()
        self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)

    def forward(self, X):
        return self.dense2(self.relu(self.dense1(X)))

下面的例子显示，改变张量的最里层维度的尺寸，会改变成基于位置的前馈网络的输出尺寸。因为用同一个多层感知机对所有位置上的输入进行变换，所以当所有这些位置的输入相同时，它们的输出也是相同的。

ffn = PositionWiseFFN(4, 4, 8)
ffn.eval()
ffn(torch.ones((2, 3, 4)))[0]

2.6.2 残差连接和层规范化

在一个小批量的样本内基于批量规范化对数据进行重新中心化和重新缩放的调整。层规范化和批量规范化的目标相同，但层规范化是基于特征维度进行规范化。尽管批量规范化在计算机视觉中被广泛应用，但在自然语言处理任务中（输入通常是变长序列）批量规范化通常不如层规范化的效果好。

以下代码对比不同维度的层规范化和批量规范化的效果。

ln = nn.LayerNorm(2)
bn = nn.BatchNorm1d(2)
X = torch.tensor([[1, 2], [2, 3]], dtype=torch.float32)
# 在训练模式下计算X的均值和方差
print('layer norm:', ln(X), '\nbatch norm:', bn(X))

layer norm: tensor([[-1.0000,  1.0000],
        [-1.0000,  1.0000]], grad_fn=<NativeLayerNormBackward0>)
batch norm: tensor([[-1.0000, -1.0000],
        [ 1.0000,  1.0000]], grad_fn=<NativeBatchNormBackward0>)

现在可以使用残差连接和层规范化来实现AddNorm类。暂退法也被作为正则化方法使用。

#@save
class AddNorm(nn.Module):
    """残差连接后进行层规范化"""
    def __init__(self, normalized_shape, dropout, **kwargs):
        super(AddNorm, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)
        self.ln = nn.LayerNorm(normalized_shape)

    def forward(self, X, Y):
        return self.ln(self.dropout(Y) + X)

残差连接要求两个输入的形状相同，以便加法操作后输出张量的形状相同。

add_norm = AddNorm([3, 4], 0.5)
add_norm.eval()
add_norm(torch.ones((2, 3, 4)), torch.ones((2, 3, 4))).shape
# torch.Size([2, 3, 4])

2.6.3 编码器

有了组成Transformer编码器的基础组件，现在可以先实现编码器中的一个层。下面的EncoderBlock类包含两个子层：多头自注意力和基于位置的前馈网络，这两个子层都使用了残差连接和紧随的层规范化。

#@save
class EncoderBlock(nn.Module):
    """Transformer编码器块"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
                 dropout, use_bias=False, **kwargs):
        super(EncoderBlock, self).__init__(**kwargs)
        self.attention = d2l.MultiHeadAttention(
            key_size, query_size, value_size, num_hiddens, num_heads, dropout,
            use_bias)
        self.addnorm1 = AddNorm(norm_shape, dropout)
        self.ffn = PositionWiseFFN(
            ffn_num_input, ffn_num_hiddens, num_hiddens)
        self.addnorm2 = AddNorm(norm_shape, dropout)

    def forward(self, X, valid_lens):
        Y = self.addnorm1(X, self.attention(X, X, X, valid_lens))
        return self.addnorm2(Y, self.ffn(Y))

正如从代码中所看到的，Transformer编码器中的任何层都不会改变其输入的形状。

X = torch.ones((2, 100, 24))
valid_lens = torch.tensor([3, 2])
encoder_blk = EncoderBlock(24, 24, 24, 24, [100, 24], 24, 48, 8, 0.5)
encoder_blk.eval()
encoder_blk(X, valid_lens).shape
# torch.Size([2, 100, 24])

下面实现的Transformer编码器的代码中，堆叠了num_layers个EncoderBlock类的实例。由于这里使用的是值范围在−1和1之间的固定位置编码，因此通过学习得到的输入的嵌入表示的值需要先乘以嵌入维度的平方根进行重新缩放，然后再与位置编码相加。

#@save
class TransformerEncoder(d2l.Encoder):
    """Transformer编码器"""
    def __init__(self, vocab_size, key_size, query_size, value_size,
                 num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
                 num_heads, num_layers, dropout, use_bias=False, **kwargs):
        super(TransformerEncoder, self).__init__(**kwargs)
        self.num_hiddens = num_hiddens
        self.embedding = nn.Embedding(vocab_size, num_hiddens)
        self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
        self.blks = nn.Sequential()
        for i in range(num_layers):
            self.blks.add_module("block"+str(i),
                EncoderBlock(key_size, query_size, value_size, num_hiddens,
                             norm_shape, ffn_num_input, ffn_num_hiddens,
                             num_heads, dropout, use_bias))

    def forward(self, X, valid_lens, *args):
        # 因为位置编码值在-1和1之间，
        # 因此嵌入值乘以嵌入维度的平方根进行缩放，
        # 然后再与位置编码相加。
        X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
        self.attention_weights = [None] * len(self.blks)
        for i, blk in enumerate(self.blks):
            X = blk(X, valid_lens)
            self.attention_weights[
                i] = blk.attention.attention.attention_weights
        return X

下面我们指定了超参数来创建一个两层的Transformer编码器。 Transformer编码器输出的形状是（批量大小，时间步数目，num_hiddens）。

encoder = TransformerEncoder(
    200, 24, 24, 24, 24, [100, 24], 24, 48, 8, 2, 0.5)
encoder.eval()
encoder(torch.ones((2, 100), dtype=torch.long), valid_lens).shape
# torch.Size([2, 100, 24])

2.6.4 解码器

Transformer解码器也是由多个相同的层组成。在DecoderBlock类中实现的每个层包含了三个子层：解码器自注意力、“编码器-解码器”注意力和基于位置的前馈网络。这些子层也都被残差连接和紧随的层规范化围绕。

正如在本节前面所述，在掩蔽多头解码器自注意力层（第一个子层）中，查询、键和值都来自上一个解码器层的输出。关于序列到序列模型（sequence-to-sequence model），在训练阶段，其输出序列的所有位置（时间步）的词元都是已知的；然而，在预测阶段，其输出序列的词元是逐个生成的。因此，在任何解码器时间步中，只有生成的词元才能用于解码器的自注意力计算中。为了在解码器中保留自回归的属性，其掩蔽自注意力设定了参数dec_valid_lens，以便任何查询都只会与解码器中所有已经生成词元的位置（即直到该查询位置为止）进行注意力计算。

class DecoderBlock(nn.Module):
    """解码器中第i个块"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
                 dropout, i, **kwargs):
        super(DecoderBlock, self).__init__(**kwargs)
        self.i = i
        self.attention1 = d2l.MultiHeadAttention(
            key_size, query_size, value_size, num_hiddens, num_heads, dropout)
        self.addnorm1 = AddNorm(norm_shape, dropout)
        self.attention2 = d2l.MultiHeadAttention(
            key_size, query_size, value_size, num_hiddens, num_heads, dropout)
        self.addnorm2 = AddNorm(norm_shape, dropout)
        self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens,
                                   num_hiddens)
        self.addnorm3 = AddNorm(norm_shape, dropout)

    def forward(self, X, state):
        enc_outputs, enc_valid_lens = state[0], state[1]
        # 训练阶段，输出序列的所有词元都在同一时间处理，
        # 因此state[2][self.i]初始化为None。
        # 预测阶段，输出序列是通过词元一个接着一个解码的，
        # 因此state[2][self.i]包含着直到当前时间步第i个块解码的输出表示
        if state[2][self.i] is None:
            key_values = X
        else:
            key_values = torch.cat((state[2][self.i], X), axis=1)
        state[2][self.i] = key_values
        if self.training:
            batch_size, num_steps, _ = X.shape
            # dec_valid_lens的开头:(batch_size,num_steps),
            # 其中每一行是[1,2,...,num_steps]
            dec_valid_lens = torch.arange(
                1, num_steps + 1, device=X.device).repeat(batch_size, 1)
        else:
            dec_valid_lens = None

        # 自注意力
        X2 = self.attention1(X, key_values, key_values, dec_valid_lens)
        Y = self.addnorm1(X, X2)
        # 编码器－解码器注意力。
        # enc_outputs的开头:(batch_size,num_steps,num_hiddens)
        Y2 = self.attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)
        Z = self.addnorm2(Y, Y2)
        return self.addnorm3(Z, self.ffn(Z)), state

为了便于在“编码器－解码器”注意力中进行缩放点积计算和残差连接中进行加法计算，编码器和解码器的特征维度都是num_hiddens。

decoder_blk = DecoderBlock(24, 24, 24, 24, [100, 24], 24, 48, 8, 0.5, 0)
decoder_blk.eval()
X = torch.ones((2, 100, 24))
state = [encoder_blk(X, valid_lens), valid_lens, [None]]
decoder_blk(X, state)[0].shape
# torch.Size([2, 100, 24])

现在我们构建了由num_layers个DecoderBlock实例组成的完整的Transformer解码器。最后，通过一个全连接层计算所有vocab_size个可能的输出词元的预测值。解码器的自注意力权重和编码器解码器注意力权重都被存储下来，方便日后可视化的需要。

class TransformerDecoder(d2l.AttentionDecoder):
    def __init__(self, vocab_size, key_size, query_size, value_size,
                 num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
                 num_heads, num_layers, dropout, **kwargs):
        super(TransformerDecoder, self).__init__(**kwargs)
        self.num_hiddens = num_hiddens
        self.num_layers = num_layers
        self.embedding = nn.Embedding(vocab_size, num_hiddens)
        self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
        self.blks = nn.Sequential()
        for i in range(num_layers):
            self.blks.add_module("block"+str(i),
                DecoderBlock(key_size, query_size, value_size, num_hiddens,
                             norm_shape, ffn_num_input, ffn_num_hiddens,
                             num_heads, dropout, i))
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, enc_valid_lens, *args):
        return [enc_outputs, enc_valid_lens, [None] * self.num_layers]

    def forward(self, X, state):
        X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
        self._attention_weights = [[None] * len(self.blks) for _ in range (2)]
        for i, blk in enumerate(self.blks):
            X, state = blk(X, state)
            # 解码器自注意力权重
            self._attention_weights[0][
                i] = blk.attention1.attention.attention_weights
            # “编码器－解码器”自注意力权重
            self._attention_weights[1][
                i] = blk.attention2.attention.attention_weights
        return self.dense(X), state

    @property
    def attention_weights(self):
        return self._attention_weights

2.6.5 训练

依照Transformer架构来实例化编码器－解码器模型。在这里，指定Transformer的编码器和解码器都是2层，都使用4头注意力。

为了进行序列到序列的学习，下面在“英语－法语”机器翻译数据集上训练Transformer模型。

num_hiddens, num_layers, dropout, batch_size, num_steps = 32, 2, 0.1, 64, 10
lr, num_epochs, device = 0.005, 200, d2l.try_gpu()
ffn_num_input, ffn_num_hiddens, num_heads = 32, 64, 4
key_size, query_size, value_size = 32, 32, 32
norm_shape = [32]

train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)

encoder = TransformerEncoder(
    len(src_vocab), key_size, query_size, value_size, num_hiddens,
    norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
    num_layers, dropout)
decoder = TransformerDecoder(
    len(tgt_vocab), key_size, query_size, value_size, num_hiddens,
    norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
    num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
# loss 0.032, 5679.3 tokens/sec on cuda:0

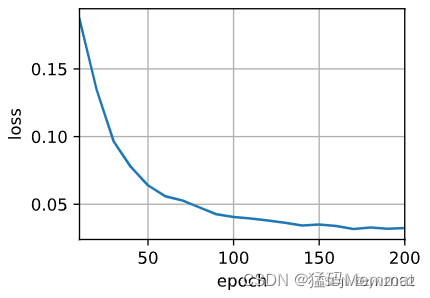
训练结束后，使用Transformer模型将一些英语句子翻译成法语，并且计算它们的BLEU分数。

engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
    translation, dec_attention_weight_seq = d2l.predict_seq2seq(
        net, eng, src_vocab, tgt_vocab, num_steps, device, True)
    print(f'{eng} => {translation}, ',
          f'bleu {d2l.bleu(translation, fra, k=2):.3f}')

go . => va !,  bleu 1.000
i lost . => j'ai perdu .,  bleu 1.000
he's calm . => il est calme .,  bleu 1.000
i'm home . => je suis chez moi .,  bleu 1.000

当进行最后一个英语到法语的句子翻译工作时，让我们可视化Transformer的注意力权重。编码器自注意力权重的形状为（编码器层数，注意力头数，num_steps或查询的数目，num_steps或“键－值”对的数目）。

enc_attention_weights = torch.cat(net.encoder.attention_weights, 0).reshape((num_layers, num_heads,
    -1, num_steps))
enc_attention_weights.shape
# torch.Size([2, 4, 10, 10])

在编码器的自注意力中，查询和键都来自相同的输入序列。因为填充词元是不携带信息的，因此通过指定输入序列的有效长度可以避免查询与使用填充词元的位置计算注意力。接下来，将逐行呈现两层多头注意力的权重。每个注意力头都根据查询、键和值的不同的表示子空间来表示不同的注意力。

d2l.show_heatmaps(
    enc_attention_weights.cpu(), xlabel='Key positions',
    ylabel='Query positions', titles=['Head %d' % i for i in range(1, 5)],
    figsize=(7, 3.5))

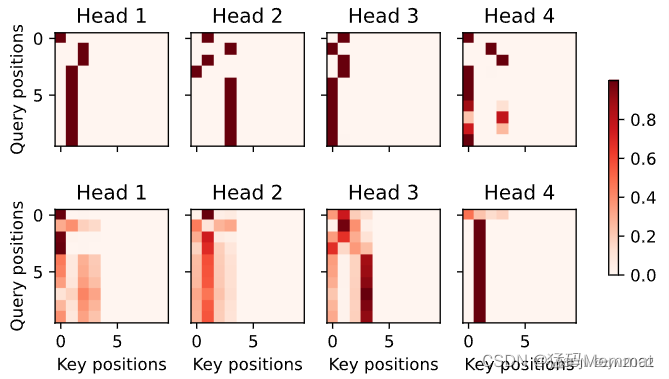
为了可视化解码器的自注意力权重和“编码器－解码器”的注意力权重，我们需要完成更多的数据操作工作。例如用零填充被掩蔽住的注意力权重。值得注意的是，解码器的自注意力权重和“编码器－解码器”的注意力权重都有相同的查询：即以序列开始词元（beginning-of-sequence,BOS）打头，再与后续输出的词元共同组成序列。

dec_attention_weights_2d = [head[0].tolist()
                            for step in dec_attention_weight_seq
                            for attn in step for blk in attn for head in blk]
dec_attention_weights_filled = torch.tensor(
    pd.DataFrame(dec_attention_weights_2d).fillna(0.0).values)
dec_attention_weights = dec_attention_weights_filled.reshape((-1, 2, num_layers, num_heads, num_steps))
dec_self_attention_weights, dec_inter_attention_weights = \
    dec_attention_weights.permute(1, 2, 3, 0, 4)
dec_self_attention_weights.shape, dec_inter_attention_weights.shape
# (torch.Size([2, 4, 6, 10]), torch.Size([2, 4, 6, 10]))

由于解码器自注意力的自回归属性，查询不会对当前位置之后的“键－值”对进行注意力计算。

# Plusonetoincludethebeginning-of-sequencetoken
d2l.show_heatmaps(
    dec_self_attention_weights[:, :, :, :len(translation.split()) + 1],
    xlabel='Key positions', ylabel='Query positions',
    titles=['Head %d' % i for i in range(1, 5)], figsize=(7, 3.5))

与编码器的自注意力的情况类似，通过指定输入序列的有效长度，输出序列的查询不会与输入序列中填充位置的词元进行注意力计算。

d2l.show_heatmaps(
    dec_inter_attention_weights, xlabel='Key positions',
    ylabel='Query positions', titles=['Head %d' % i for i in range(1, 5)],
    figsize=(7, 3.5))

尽管Transformer架构是为了序列到序列的学习而提出的，但Transformer编码器或Transformer解码器通常被单独用于不同的深度学习任务中。

• 小结

1. Transformer是编码器－解码器架构的一个实践，尽管在实际情况中编码器或解码器可以单独使用。
2. 在Transformer中，多头自注意力用于表示输入序列和输出序列，不过解码器必须通过掩蔽机制来保留自回归属性。
3. Transformer中的残差连接和层规范化是训练非常深度模型的重要工具。
4. Transformer模型中基于位置的前馈网络使用同一个多层感知机，作用是对所有序列位置的表示进行转换。

3. pytorch中的注意力机制类

3.1 torch.nn.MultiheadAttention

Class:
torch.nn.MultiheadAttention(embed_dim, num_heads, dropout=0.0, bias=True, add_bias_kv=False, add_zero_attn=False, kdim=None, vdim=None, batch_first=False, device=None, dtype=None)

4. Transformer 在计算机视觉领域的应用

4.1 Vision Transformer

4.1.1 ViT的总体结构

下图是原论文中给出的关于Vision Transformer(ViT)的模型框架。简单而言，模型由三个模块组成：

• Linear Projection of Flattened Patches(Embedding层)
• Transformer Encoder(图右侧有给出更加详细的结构)
• MLP Head（最终用于分类的层结构）
  

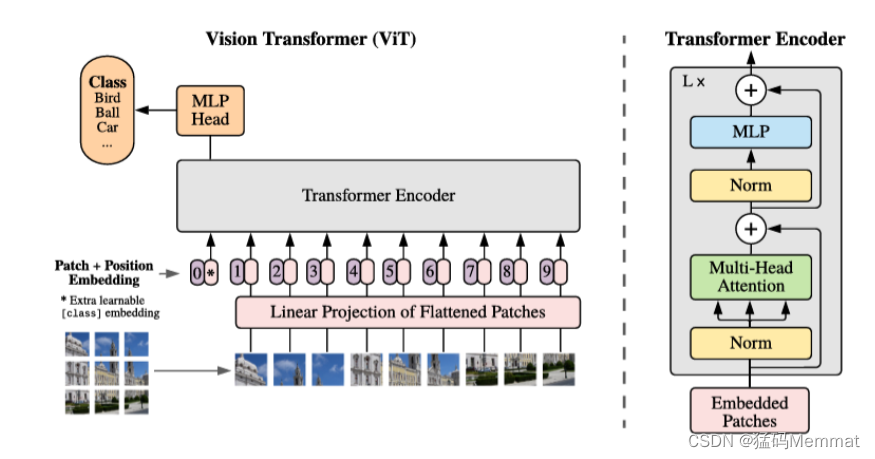
4.1.2 Embedding层结构详解

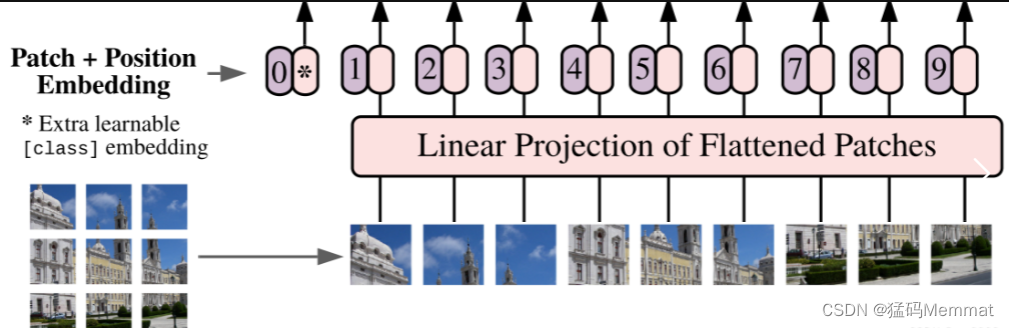
4.1.3 Transformer Encoder详解

4.1.4 MLP Head详解

上面通过Transformer Encoder后输出的shape和输入的shape是保持不变的，以ViT-B/16为例，输入的是[197, 768]输出的还是[197, 768]。注意，在Transformer Encoder后其实还有一个Layer Norm没有画出来。这里我们只是需要分类的信息，所以我们只需要提取出[class]token生成的对应结果就行，即[197, 768]中抽取出[class]token对应的[1, 768]。接着我们通过MLP Head得到我们最终的分类结果。MLP Head原论文中说在训练ImageNet21K时是由Linear+tanh激活函数+Linear组成。但是迁移到ImageNet1K上或者你自己的数据上时，只用一个Linear即可。

4.2 Swin Transformer

论文：《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》
代码：https://github.com/microsoft/Swin-Transformer

4.2.1 网络的整体框架

首先，先来简单对比下Swin Transformer和之前的Vision Transformer。

• Swin Transformer使用了类似卷积神经网络中的层次化构建方法（Hierarchical feature maps），比如特征图尺寸中有对图像下采样4倍的，8倍的以及16倍的，这样的backbone有助于在此基础上构建目标检测，实例分割等任务。而在之前的Vision Transformer中是一开始就直接下采样16倍，后面的特征图也是维持这个下采样率不变。
• 在Swin Transformer中使用了Windows Multi-Head Self-Attention(W-MSA)的概念，比如在下图的4倍下采样和8倍下采样中，将特征图划分成了多个不相交的区域（Window），并且Multi-Head Self-Attention只在每个窗口（Window）内进行。相对于Vision Transformer中直接对整个（Global）特征图进行Multi-Head Self-Attention，这样做的目的是能够减少计算量的，尤其是在浅层特征图很大的时候。这样做虽然减少了计算量但也会隔绝不同窗口之间的信息传递，所以在论文中作者又提出了 Shifted Windows Multi-Head Self-Attention(SW-MSA)的概念，通过此方法能够让信息在相邻的窗口中进行传递，后面会细讲。
  
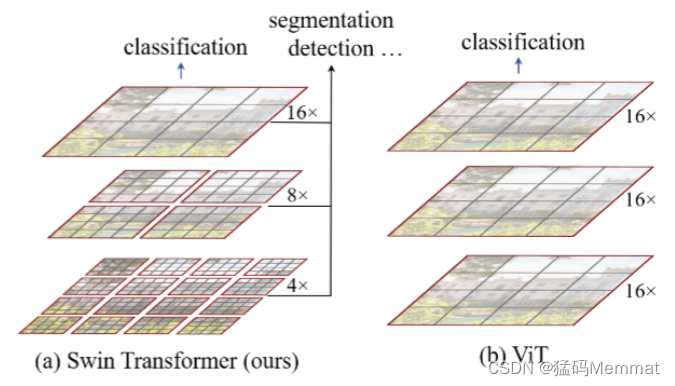
  接下来，简单看下原论文中给出的关于Swin Transformer（Swin-T）网络的架构图。通过图(a)可以看出整个框架的基本流程如下：
  
  

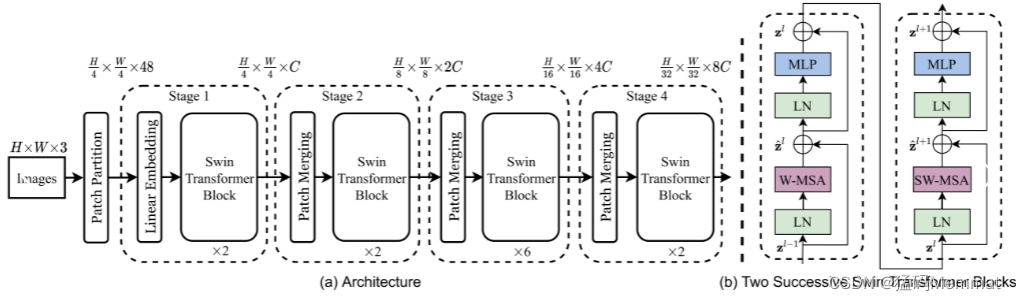
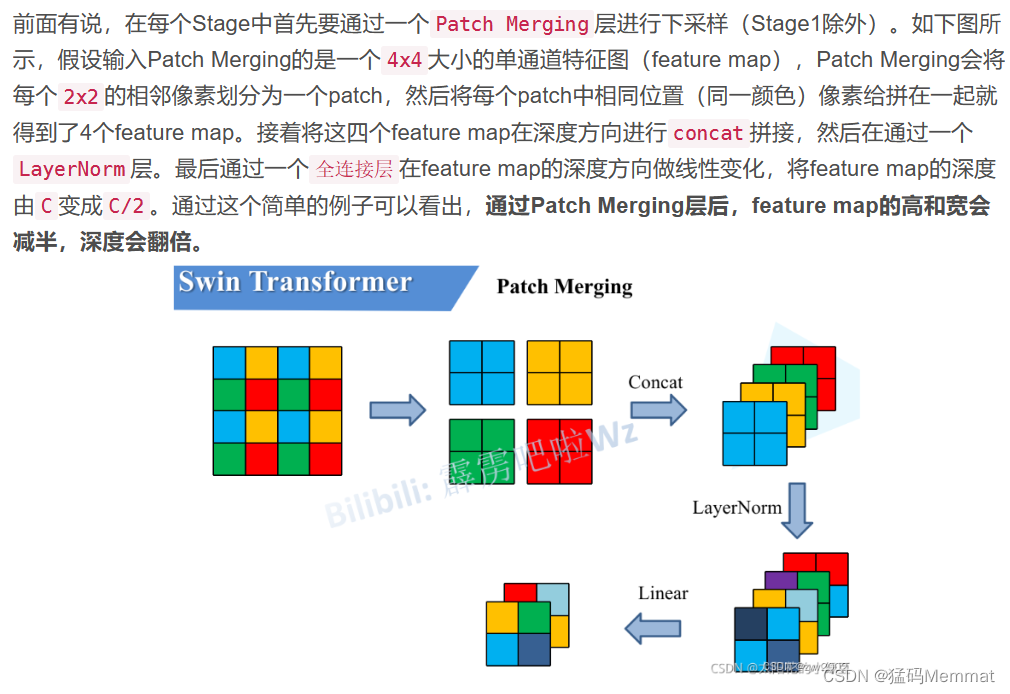
4.2.2 Patch Mering

4.2.3 W-MSA

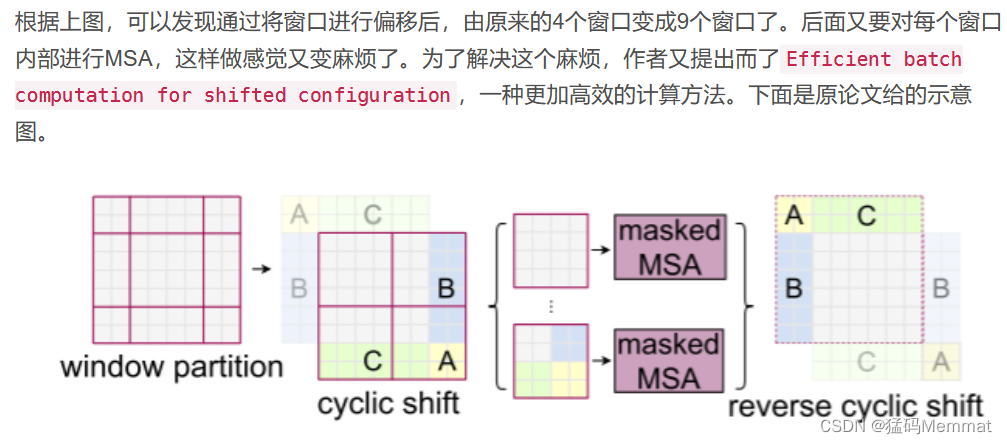
4.2.4 SW-MSA

参考文献

转载自原文：https://blog.csdn.net/zyw2002/article/details/128788680

---

本文代码主要参考了李沐老师的《Dive into Deep Learning》书中的两节内容
现代循环神经网络：https://zh.d2l.ai/chapter_recurrent-modern/index.html
注意力机制：https://zh.d2l.ai/chapter_attention-mechanisms/index.html

---

本文中的讲解和图片部分源自李宏毅老师的机器学习课程
【機器學習2021】自注意力機制 (Self-attention) (上)：https://www.youtube.com/watch?v=hYdO9CscNes&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index=10
【機器學習2021】自注意力機制 (Self-attention) (下)
【機器學習2021】Transformer (上)
【機器學習2021】Transformer (下)

---

本文中的图解部分源自：Jay Alammar 的两篇文章
《The Illustrated Transformer》：https://jalammar.github.io/illustrated-transformer/

《Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention)》：https://jalammar.github.io/visualizing-neural-machine-translation-mechanics-of-seq2seq-models-with-attention/

---

其他关于Transformer的讲解，参考的有如下文章
Transformer模型详解（图解最完整版）：https://zhuanlan.zhihu.com/p/338817680

史上最小白之Transformer详解：https://blog.csdn.net/Tink1995/article/details/105080033

---

pytorch 文档-torch.nn.MultiheadAttention：https://pytorch.org/docs/stable/generated/torch.nn.MultiheadAttention.html#torch.nn.MultiheadAttention

---

Transformer在计算机视觉中的应用参考：
《Vision Transformer 详解》：https://blog.csdn.net/qq_37541097/article/details/118242600

《Swin Transformer 详解》：https://blog.csdn.net/qq_37541097/article/details/121119988