知识储备

无监督聚类缺点

聚类不同于其他常见机器学习有监督方法，聚类为一种无监督学习方法，原理为随机选取K个质心（K为确定聚类的数目），计算距离质心最近的样本点，不断迭代更新质心。不断地将样本点划分为K种类别。
但常见无监督聚类会为0-1聚类，即为并未对聚类边缘样本点进行再判断。
常见聚类算法如K-means需要确定簇类数目。因此如果制定了错误的簇数量，实验结果以及正确识别率会比较差。因此无监督聚类算法最重要的是确定合适的簇类数目K。

无监督聚类的评价指标

聚类的目的是对样本点进行正确分类。因此所需要达到的目的如下所示。

1. 聚类中同一类别的点尽可能接近该聚类质心。
2. 属于不同类别的点尽可能远离其他聚类质心。

在理想情况下，聚类结果为簇内变化较小，簇间变化较大。因此，无监督聚类的质量评价指标如下所示。

• inertia（惯性)，用于计算数据点与所属聚类中心之间的平方距离之和，主要呈现的是簇内之间的变化。
• silhouette coefficient 轮廓系数，轮廓系数主要用于体现簇内和簇间的变化

1. 数据点到所属聚类中心的距离，假设为$d_{near}$
2. 数据点到次优聚类中心的距离（个人认为是当前数据点距离聚类中心最近，且不为所属聚类中心的其他点），假设为$d_{next}$
   计算公式轮廓$S=\frac{d_{next}-d_{near}}{max(d_{near},d_{next})}$，max()方法为求取最大值。若S接近1，证明该聚类算法能够较好的将数据分离为良好的聚类。

常见确定簇数K的方法

1. 尝试不同数量的簇的r聚类算法，寻找最优的聚类效果，并将设置的簇数K参数确定为正确的簇类数目。
2. 肘部法则 （The elbow method）
3. 轮廓系数 （the optimization of the silhouette coefficient）

肘部法则

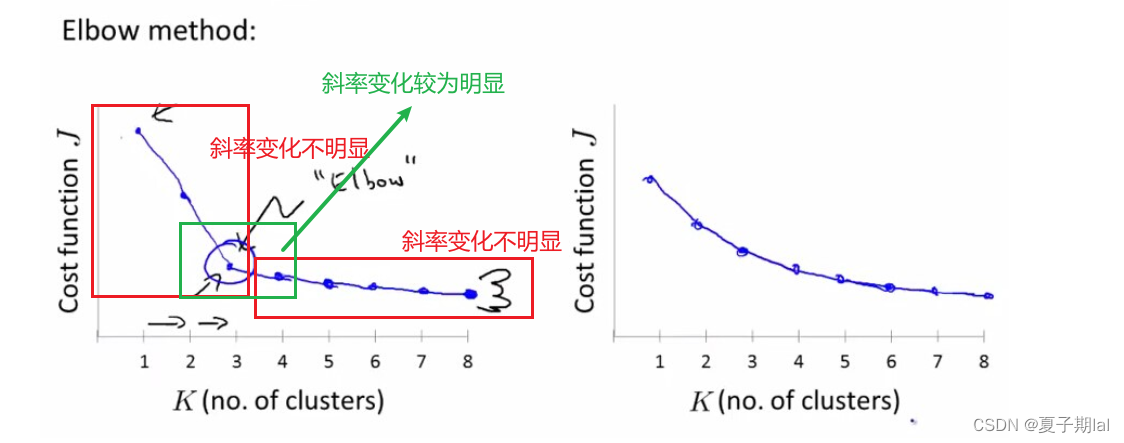
我们主要通过计算在不同情况下的K值的平均cost function（损失函数）变化从而得出明显变化拐点（inertia点）。
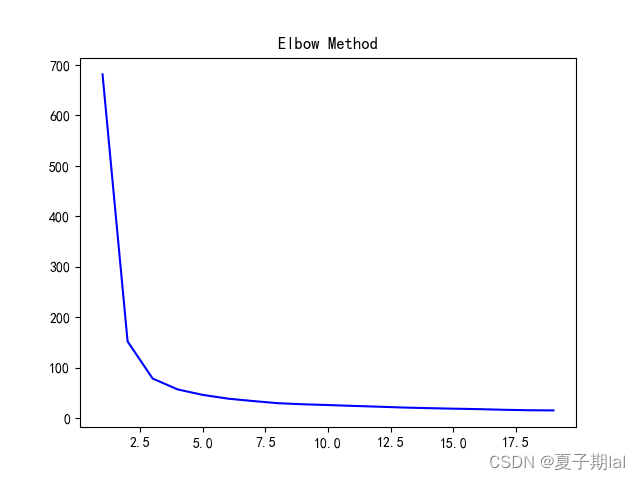
cost function的大小主要与簇数K有关，不同的K之间，inertia曲线的斜率是不同的。具体如图所示。但拐点寻找较为主观。因此肘部法则只能解决部分的确定最有的簇类数目。

代码实现

from sklearn.cluster import KMeans, AgglomerativeClustering,DBSCAN
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import matplotlib
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.decomposition import PCA
iris = load_iris()
# 获取数据集中的特征向量
data = iris.data
elbow = []
for i in range(1, 20):  # 创建遍历，找到最合适的k值
   kmeans = KMeans(n_clusters=i, init='k-means++', random_state=101)
   kmeans.fit(data)
   elbow.append(kmeans.inertia_)
# 通过画图找出最合适的K值
k_num = [i for i in range(1, 20)]
plt.plot(k_num, elbow, color='blue')
plt.rcParams.update({'figure.figsize': (16, 10), 'figure.dpi': 100})
plt.title('Elbow Method')
plt.show()

具体的结果如图所示。

轮廓系数

silhouette coefficient 轮廓系数，轮廓系数主要用于体现簇内和簇间的变化。具体公式以及原理如下所示。若S接近1，证明该聚类算法能够较好的将数据分离为良好的聚类。

1. 数据点到所属聚类中心的距离，假设为$d_{near}$
2. 数据点到次优聚类中心的距离（个人认为是当前数据点距离聚类中心最近，且不为所属聚类中心的其他点），假设为$d_{next}$
   计算公式轮廓$S=\frac{d_{next}-d_{near}}{max(d_{near},d_{next})}$，max()方法为求取最大值。

代码实现

from sklearn.cluster import KMeans, AgglomerativeClustering,DBSCAN
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import matplotlib
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.decomposition import PCA
iris = load_iris()
# 获取数据集中的特征向量
data = iris.data
 from sklearn import metrics
 # 创建遍历，找到最合适的k值
 scores = []
 for k in range(2, 20):
     labels = KMeans(n_clusters=k).fit(data).labels_
     score = metrics.silhouette_score(data, labels)
     scores.append(score)
 # 通过画图找出最合适的K值
 k_num = list(range(2, 20))
 plt.plot(k_num, scores)
 plt.xlabel('Number of Clusters Initialized')
 # 设置坐标轴的的呈现形式
 plt.xticks(np.arange(0, 20, 1))
 plt.ylabel('Sihouette Score')
 plt.show()

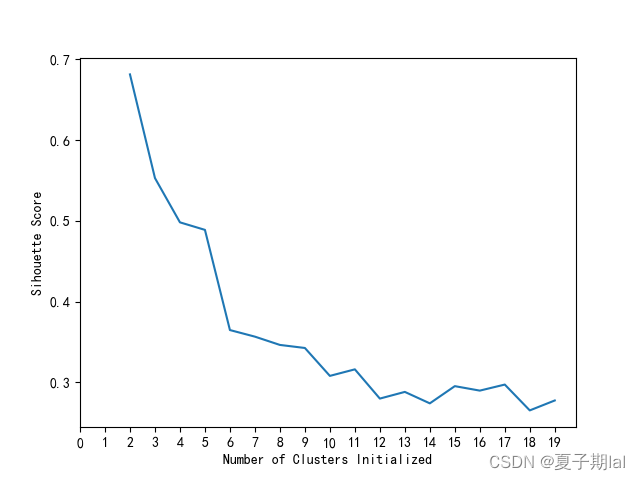
具体代码效果如下所示。

参考

python实现肘部法则和轮廓系数可视化
如何确定多少个簇？聚类算法中选择正确簇数量的三种方法
K-Means算法之K值的选择