ResNet (Residual Network)
此网络于2015年,国人何先生提出,用于解决随着深度学习的层数加深造成的网络退化现象和梯度消失、梯度爆炸。
问题1 退化现象
当深度学习的各项指标能够随着训练轮数收敛的情况下,网络的层数增强未能像理论一样:"抽象出更具有语义的特征,从而比层数少的网络准确率高。"反而准确率是下降的。
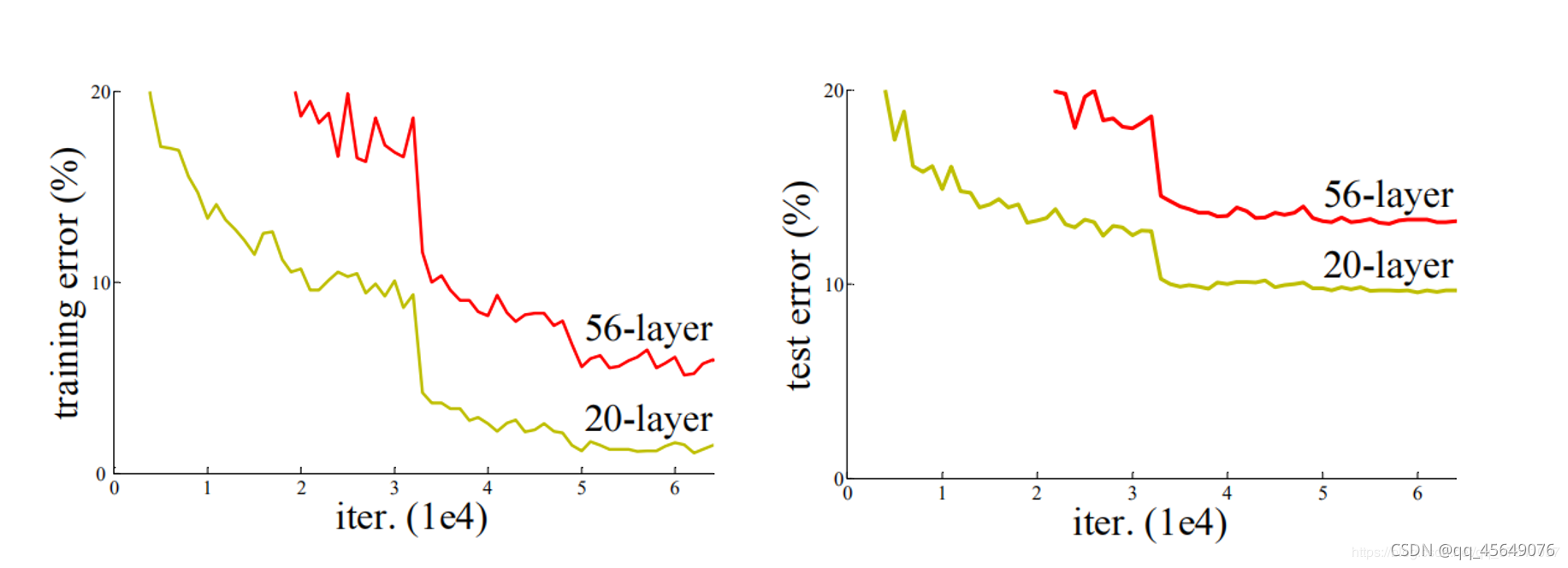
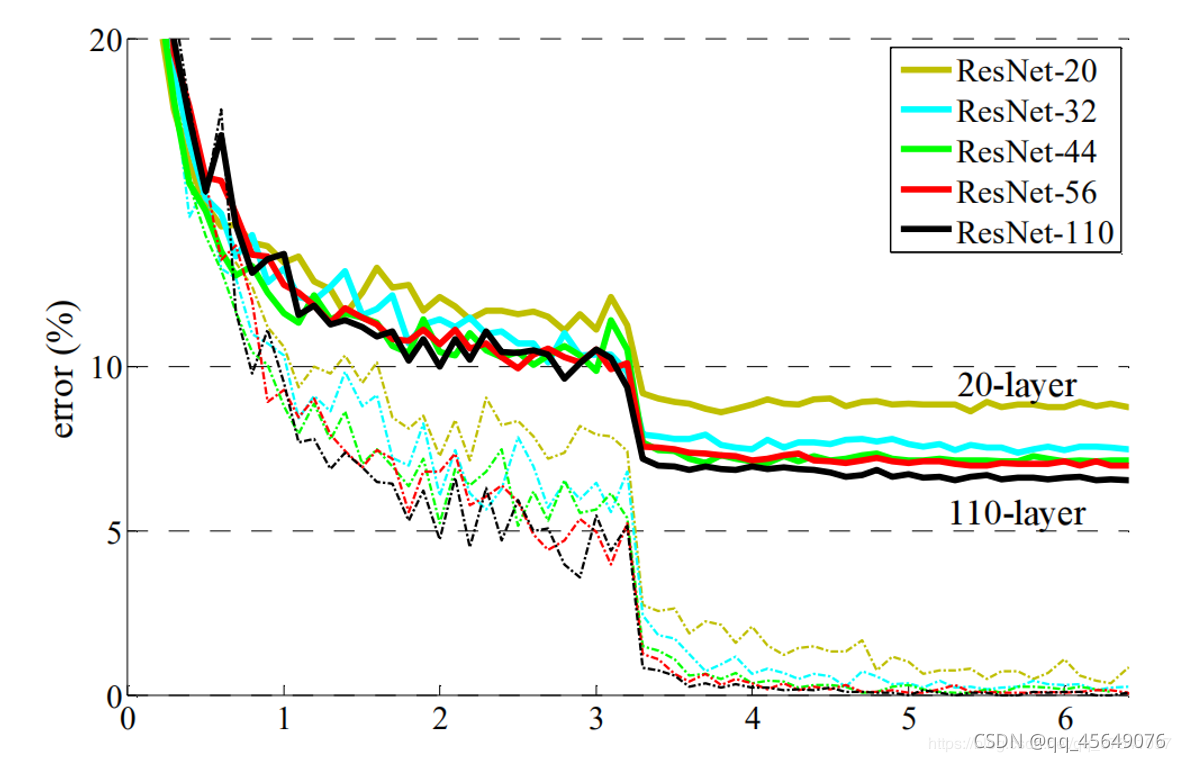
可以看到这并不是因为过拟合引起的测试准确率下降,因为训练时同样效果不佳。
解决方案:采用两种residual网络结构来加强数据原始数据与最终输出特征的关联度,弱化层之间的强联系,允许跳跃链接。
下图中虚线代表采用了residual的深度学习网络,可以看到,良好的解决了网络退化的问题。
BasicBlock和Bottleneck
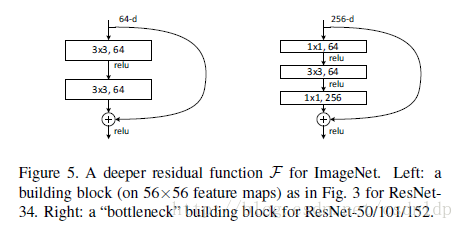
左侧残差结构称为 BasicBlock,右侧残差结构称为 Bottleneck。
从参数量的对比上来看,假设我们都是输入256通道的数据,那么
CNN参数个数 = 卷积核尺寸×卷积核深度 × 卷积核组数 = 卷积核尺寸 × 输入特征矩阵深度 × 输出特征矩阵深度
BasicBlock,参数的个数是:256×256×3×3+256×256×3×3=1179648
Bottleneck,参数的个数是:1×1×256×64+3×3×64×64+1×1×256×64=69632
考虑参数量,通常在深层时会采用三层的resnet结构
Shortcut connection
上图中的“跨层链接”称为短路链接:Shortcut connection。
短路连接 H(x) = F(x) + x 这里需要逐元素加和,如果 F(x) 与 x 的通道数相同,则可以直接相加(对应实线),如果 F(x) 与 x 的通道数不同,则需要进行维度匹配。
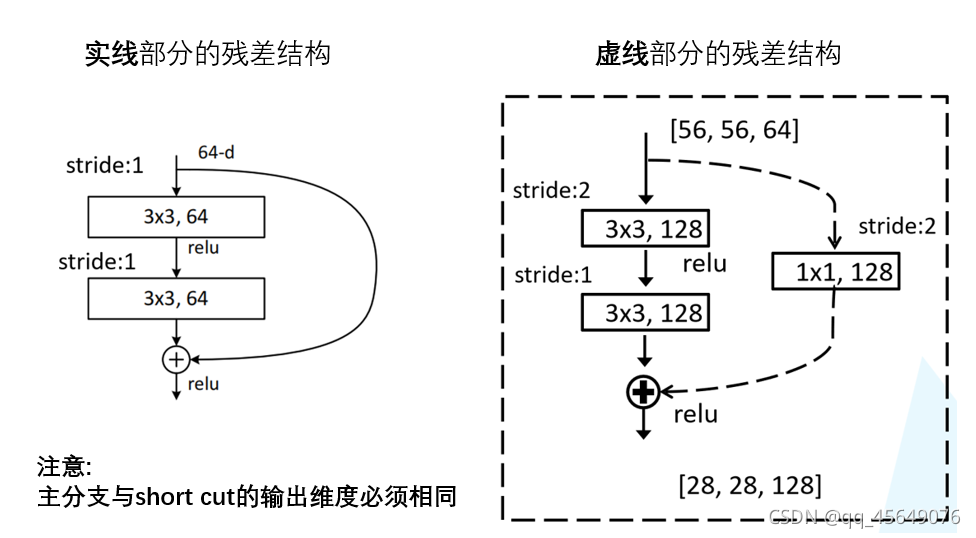
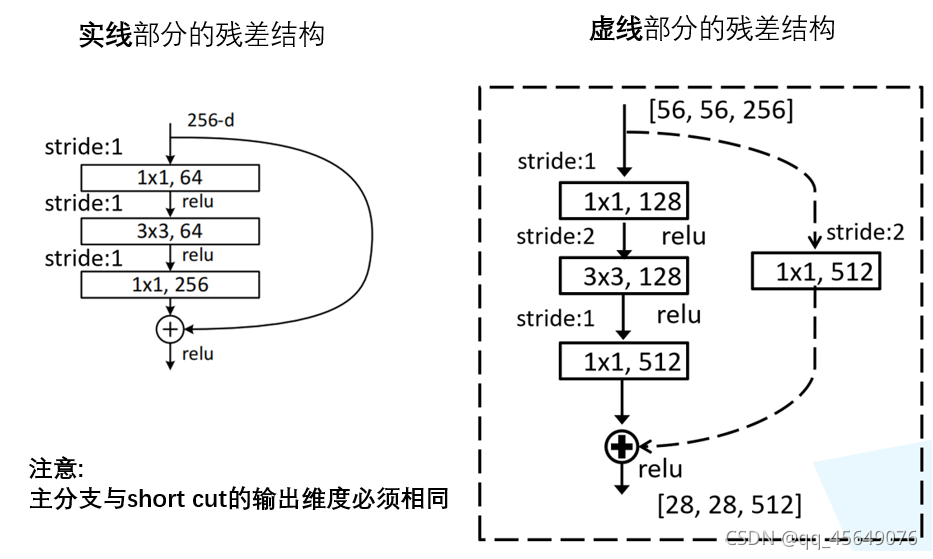
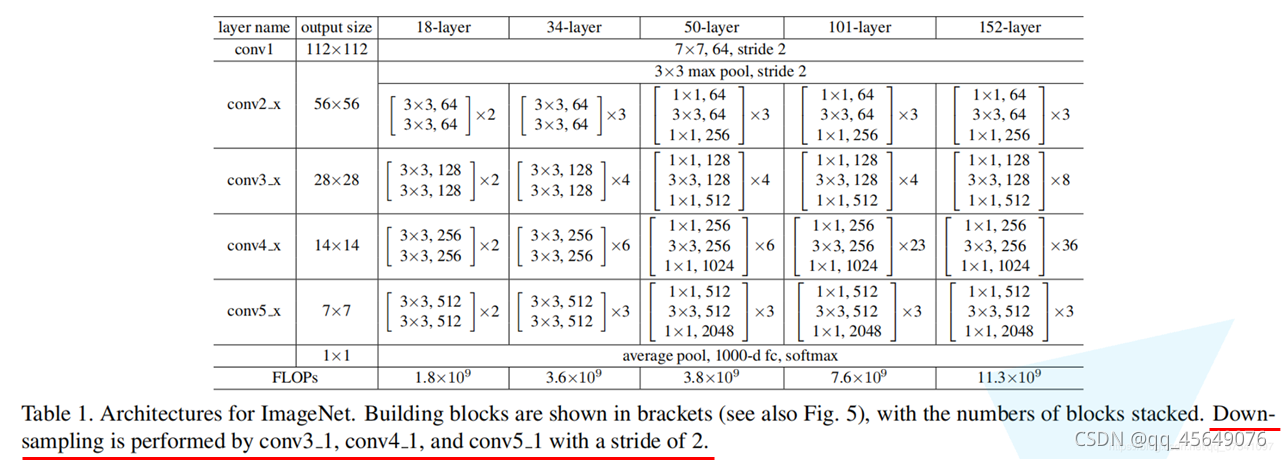
原文的标注中已说明,conv3_x, conv4_x, conv5_x所对应的一系列残差结构的第一层残差结构都是虚线残差结构。因为这一系列残差结构的第一层都有调整输入特征矩阵shape的使命(将特征矩阵的高和宽缩减为原来的一半,将深度channel调整成下一层残差结构所需要的channel)
原文中的shortcut三种实现方案。
(A)“zero-padding shortcuts are used for increasing dimensions, and all shortcuts are parameterfree”
两者维度(通道数)不同,可对增加的维度使用零填充(使用全0填充缺少的维度, 然后concat低维数据从而升到高维)。
(B)“projection shortcuts are used for increasing dimensions, and other shortcuts are identity”
两者维度(通道数)不同,可采用论文中提到的公式H(x) = F(x) + Wx来匹配维度,其中 W 代表线性投影(使用 1x1 卷积),其他shortcuts则为恒等映射(维度相同时)。
(C)“all shortcuts are projections”
无论维度是否相同,对于所有的shortcuts,都使用 1x1 卷积来匹配维度。
问题2 梯度消失、梯度爆炸
梯度消失:若每一层的误差梯度小于1,反向传播时,网络越深,梯度越趋近于0
梯度爆炸:若每一层的误差梯度大于1,反向传播时,网络越深,梯度越来越大
解决方案:Batch normalization(批(数据)归一化)
Batch Normalization是指批标准化处理,将一批数据的所有的feature map满足均值为0,方差为1的分布规律。它不仅可以加快了模型的收敛速度,而且更重要的是在一定程度缓解了深层网络中“梯度弥散(特征分布较散)”的问题。
在BN出现之前,数据归一化一般都在数据输入层,对输入数据进行求均值以及求方差做归一化。
BN的出现使我们可以在网络中任意一层对数据归一化处理。我们现在所用的优化方法大多都是min-batch SGD,所以我们的归一化操作就成为Batch Normalization。
BN中的数据归一化是在正态分布式的归一化的基础上进行的修改,步骤如下:

1.求每一个训练批次数据的均值
2.求每一个训练批次数据的方差
3.使用均值和方差对该批次的训练数据做归一化,获得(0,1)正态分布。其中ε是为了避免除数为0时所使用的微小正数。
由于归一化后的xi基本会被限制在正态分布下,使得网络的表达能力下降。为解决该问题,我们引入两个新的参数:γ,β。
γ是尺度因子,β是平移因子,在训练时网络学习得到。
4.尺度变换和偏移:将xi乘以γ调整数值大小,再加上β增加偏移后得到yi。
1-3步如下

左图是没有经过任何处理的输入数据,曲线是sigmoid函数,如果数据在梯度很小的区域,那么学习率就会很慢甚至陷入长时间的停滞。若是使用均值和方差进行归一化,则如右图所示,这会让数据总是在中心一片梯度最大的区域,这是对抗梯度消失的一种有效手段(ReLU),如果对于多层数据做归一化,则可将数据分布忽略提高收敛速度。
BN方法的第四步

为什么要有第四步尺度变换与偏移?
减均值除方差得到的分布是正态分布,不能认为这样得到的正太分布就是最符合我们训练样本特征的分布的函数曲线。比如数据本身就很不对称,或者激活函数未必是对方差为1的数据最好的效果,比如Sigmoid激活函数,在-1~1之间的梯度变化不大,那么非线性变换的作用就不能很好的体现。也就是说,减均值除方差操作后可能会削弱网络的性能。因此要引入第四步,改变方差大小和均值位置,使得新的分布更切合数据的真实分布,保证模型的非线性表达能力。
BN的本质,第四步操作和均值方差的关系是什么?
而第四步的本质或者说BN的本质是利用优化,改变方差大小和均值位置,使得新的分布更切合数据的真实分布,保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差,那么经过batch normalization之后的数据和输入完全一样,当然一般的情况是不同的。
预测时BN所使用的均值和方差来源于那里?
在训练时,我们会对同一批的数据的均值和方差进行求解,进而进行归一化操作。对于预测阶段时所使用的均值和方差,也是来源于训练集。在模型训练时我们记录下每个batch的均值和方差,训练完毕后,求整个训练样本的均值和方差期望值作为进行预测时,进行BN的的均值和方差。