寻找重复数-快慢指针

news2025/1/12 13:45:48

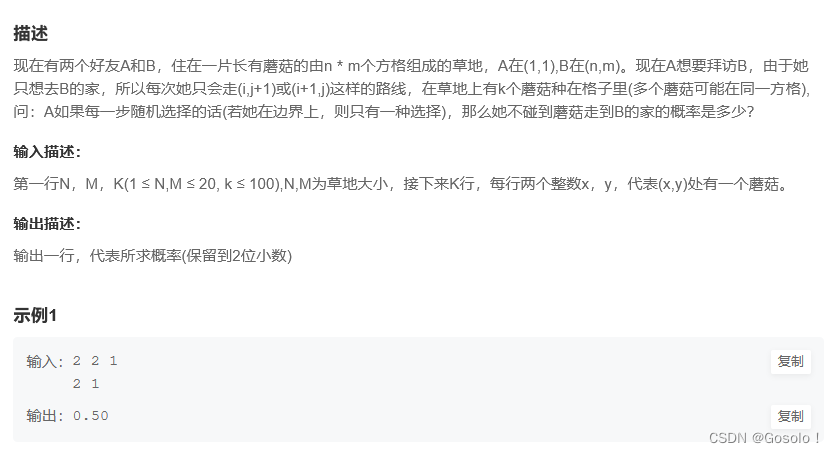
给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有一个重复的整数，返回这个重复的数。

你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

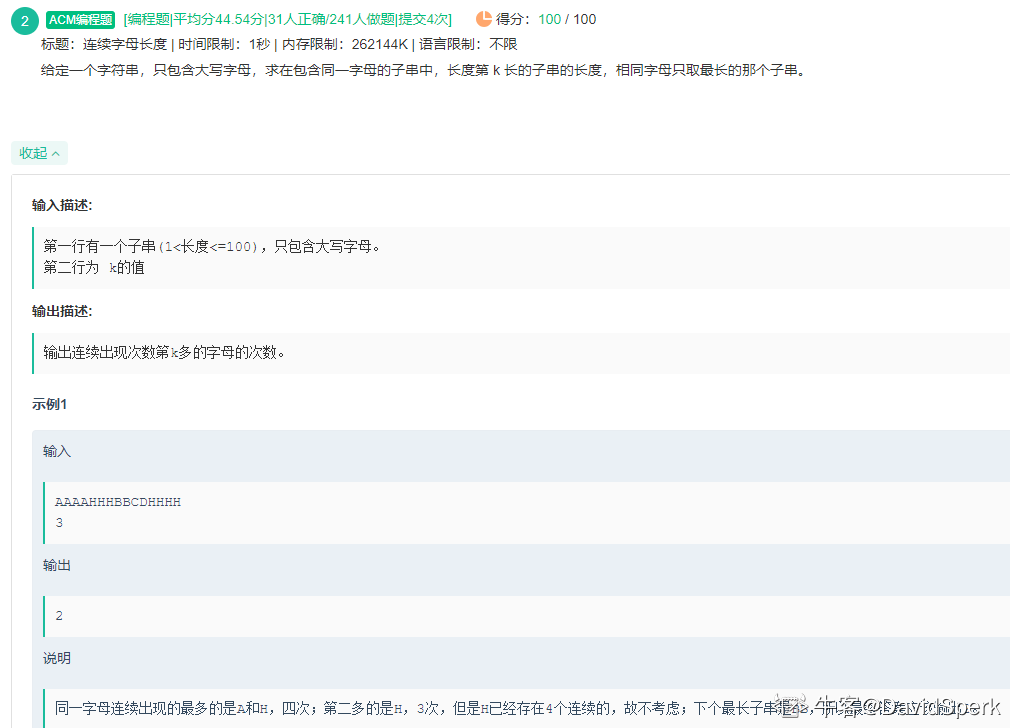
示例 1：

输入：nums = [1,3,4,2,2]
输出：2
示例 2：

输入：nums = [3,1,3,4,2]
输出：3

提示：

1 <= n <= $10^5$
nums.length == n + 1
1 <= nums[i] <= n
nums 中只有一个整数出现两次或多次，其余整数均只出现一次

进阶：

如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

数组形式的链表

题目设定的问题是 N+1 个元素都在 [1,n] 这个范围内。这样我们可以用那个类似于 ‘缺失的第一个正数’ 这种解法来做，但是题意限制了我们不能修改原数组，我们只能另寻他法。也就是本编题解讲的方法，将这个题目给的特殊的数组当作一个链表来看，数组的下标就是指向元素的指针，把数组的元素也看作指针。如 0 是指针，指向 nums[0]，而 nums[0] 也是指针，指向 nums[nums[0]].
这样我们就可以有这样的操作

int point = 0;
while(true){
    point = nums[point]; // 等同于 next = next->next; 
}

链表中的环

假设有这样一个样例：[1,2,3,4,5,6,7,8,9,5]。如果我们按照上面的循环下去就会得到这样一个路径: 1 2 3 4 5 [6 7 8 9] [6 7 8 9] [6 7 8 9] . . .这样就有了一个环，也就是6 7 8 9。point 会一直在环中循环的前进。
这时我们设置两个一快(fast)一慢(slow)两个指针，一个每次走两步，一个每次走一步，这样让他们一直走下去，直到他们在重复的序列中相遇

在这里插入图片描述

int fast = 0, slow = 0;
while(true){
    fast = nums[nums[fast]];
    slow = nums[slow];
    if(fast == slow)
        break;
}

如上图，slow和fast会在环中相遇，先假设一些量：起点到环的入口长度为m，环的周长为c，在fast和slow相遇时slow走了n步，则fast走了2n步，fast比slow多走了n步，而这n步全用在了在环里循环（n%c==0）。当fast和last相遇之后，我们设置第三个指针finder，它从起点开始和slow(在fast和slow相遇处)同步前进，当finder和slow相遇时，就是在环的入口处相遇，也就是重复的那个数字相遇。

为什么 finder 和 slow 相遇在入口
fast 和 slow 相遇时，slow 在环中行进的距离是n-m，其中 n%c0。这时我们再让 slow 前进 m 步——也就是在环中走了 n 步了。而 n%c0 即 slow 在环里面走的距离是环的周长的整数倍，就回到了环的入口了，而入口就是重复的数字。
我们不知道起点到入口的长度m，所以弄个 finder 和 slow 一起走，他们必定会在入口处相遇。

class Solution:
    def findDuplicate(self, nums: list) -> int:
        slow, fast = 0, 0
        while True:
            slow = nums[slow]
            fast = nums[nums[fast]]
            if slow == fast:
                break
        finder = 0
        while True:
            finder = nums[finder]
            slow = nums[slow]
            if finder == slow:
                break
        return finder