文章目录
- 前言
- 向量
- 矩阵
- 行列式
- 线性方程
- 非方阵
- 点积
- 叉积
前言
最近在复习线代,李永乐的基础课我刷了一下,感觉讲的不够透彻,和我当年学线代的感觉一样,就是不够形象。
比如,行列式为什么那么重要,它的含义究竟是什么?特征值到底代表了什么?等等。说白了,我需要几何直观的理解。
几何直观解决的问题是,我为什么要用这个,有什么用,而数值计算只是让我们能应用罢了,可惜我们只是学了数值计算。
于是我开始刷3b1b的《线性代数的本质》
这篇文章是观看视频后我的个人感悟,可以结合视频一起食用,有解释的不清楚的地方,以视频为准。
线性代数的本质
向量
在线性代数中,向量是以原点为起点的箭头,终点坐标和向量的值是一样的。
因此,向量之间的空间上的运算也可以变成向量值的运算,比如向量和(移动),向量数乘(缩放)。
之所以能够用向量对应向量值,是因为有一个i和j的基底。说白了,就是坐标系。如果基底变了,要保持向量不变的话,向量值就要改变。
总之,用数值(向量值)描述向量,要依赖于基底。
如果两个基底不共线(线性无关),则可以张成一个面,否则只能是一条线
如果是三个线性无关的向量,则可以张成一个三维空间,如果是n个线性无关的向量,则可以张成n维空间,但是这个就是无法想象的了。
如何理解线性相关呢?所谓线性相关,就是说某一个向量落在了其他向量张成的空间内,不需要这个向量了,可以移除这个向量而不影响向量组张成的空间。
假设给定3个向量的向量组,假设两个向量共线,那么必然线性相关(充分条件),但是如果三个向量都不共线,就能说明线性无关了吗?不能。
下面4条等价:
- 线性相关
- 有一个向量落在其他两个向量张成的平面内
- 该向量可以被其他向量线性表出
- 存在不全为0的k,使得
k 1 α 1 + ⋯ + k n α n = 0 k_1\alpha_1+\cdots+k_n\alpha_n=0 k1α1+⋯+knαn=0
前面的都好理解,第4条可以这么理解,基于3,可以得到第i个向量=其他向量的线性组合,那么令 k i = − 1 k_i=-1 ki=−1,不就是一组不全为0的系数,让这个向量组的计算结果=0吗?
矩阵
矩阵有两种含义
- 向量组
- 对向量的线性变换
给定一个向量,乘一个矩阵,就可以变成新向量,这就是矩阵的几何意义。
当一个矩阵里面的所有向量被同时变换,那就是矩阵的线性变换。
但是无论是向量,还是矩阵,其变换都是通过乘以矩阵实现的。
实际上任何函数都可以变换空间,只是线性变换后,曾经的直线还是直线,原点也没有变化。本质在于,线性变换是均匀的,保持网格线平行且等距均匀分布的变换。
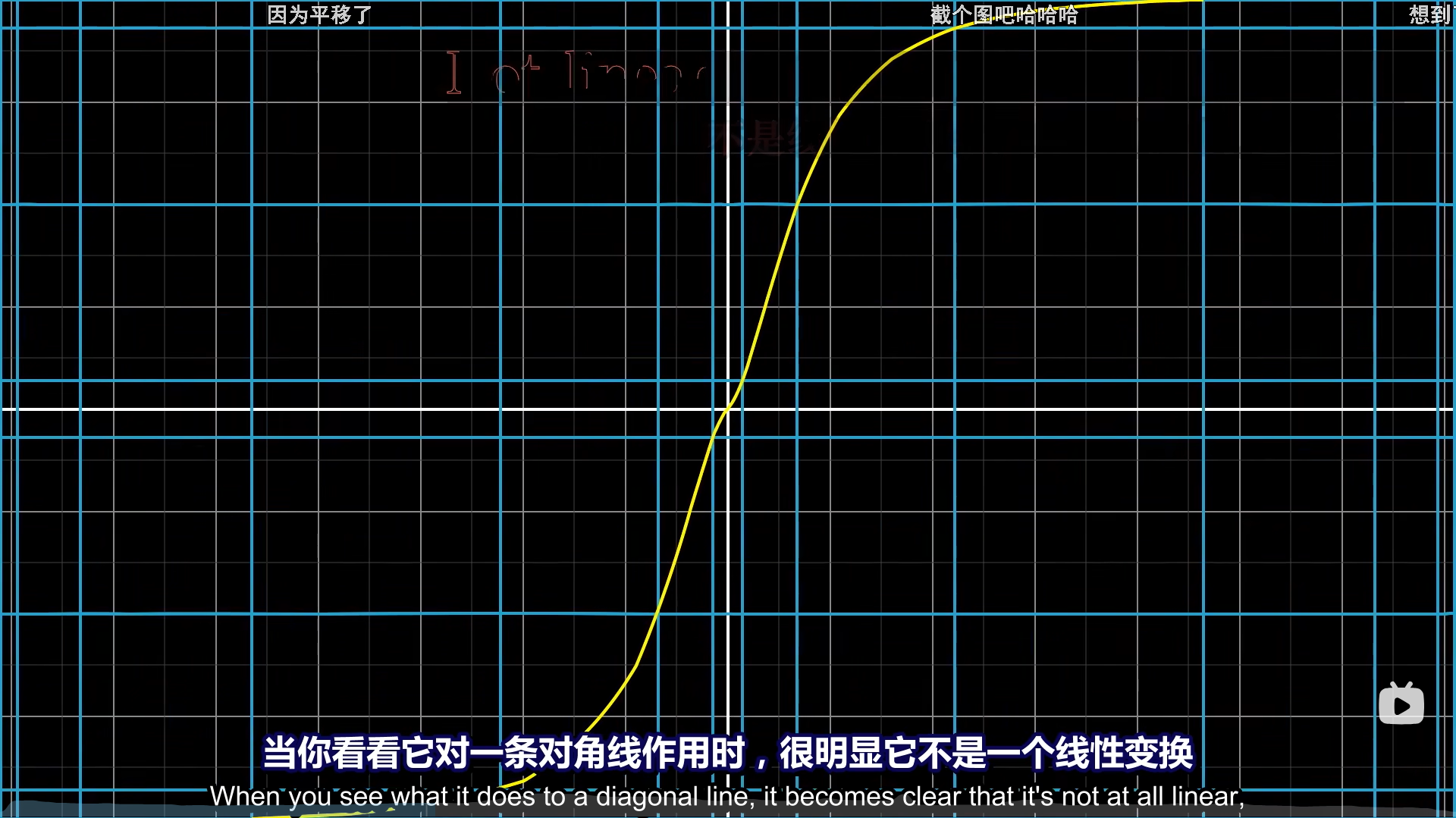
用另一个说法去说,就是基底是线性变换的,而曾经的所有向量与基底的关系保持不变,变的,只是向量本身的值,而不是向量和基底的关系。
所以考虑线性变换,我们其实只需要记住两个事情:
- 原始向量和原始基底的关系,这个关系会保持不变
- 基底的情况,这会随着线性变换而变
这两点注意好,无论你怎么变基底,都可以迅速推断出新向量的位置
实际上,对于二维来说,一个向量本身就是 ( i ^ , j ^ ) [ k 1 k 2 ] = k 1 i ^ + k 2 j ^ (\hat{i},\hat{j}) \begin{bmatrix} k_1\\k_2\end{bmatrix}=k_1\hat{i}+k_2\hat{j} (i^,j^)[k1k2]=k1i^+k2j^
而 ( i ^ , j ^ ) (\hat{i},\hat{j}) (i^,j^)本身就是一个矩阵, [ 1 0 0 1 ] \begin{bmatrix} 1\ 0\\ 0\ 1 \end{bmatrix} [1 00 1]
可以直观地理解:
- 左边的矩阵,从左到右是n个基底
- 右边的向量代表向量和基底的关系,就是线性标出的系数
- 新的向量就是新的基底的线性组合,最后算出来的值,就是新的基底下,向量的值。
- 新向量按照维度理解,则每一个维度,都是基底按照系数线性组合的结果
进一步总结:任何一个向量都等于基底乘以系数向量,包括最开始的i,j基底。

通过这个思路,就可以理解,旋转和剪切是如何实现的了。
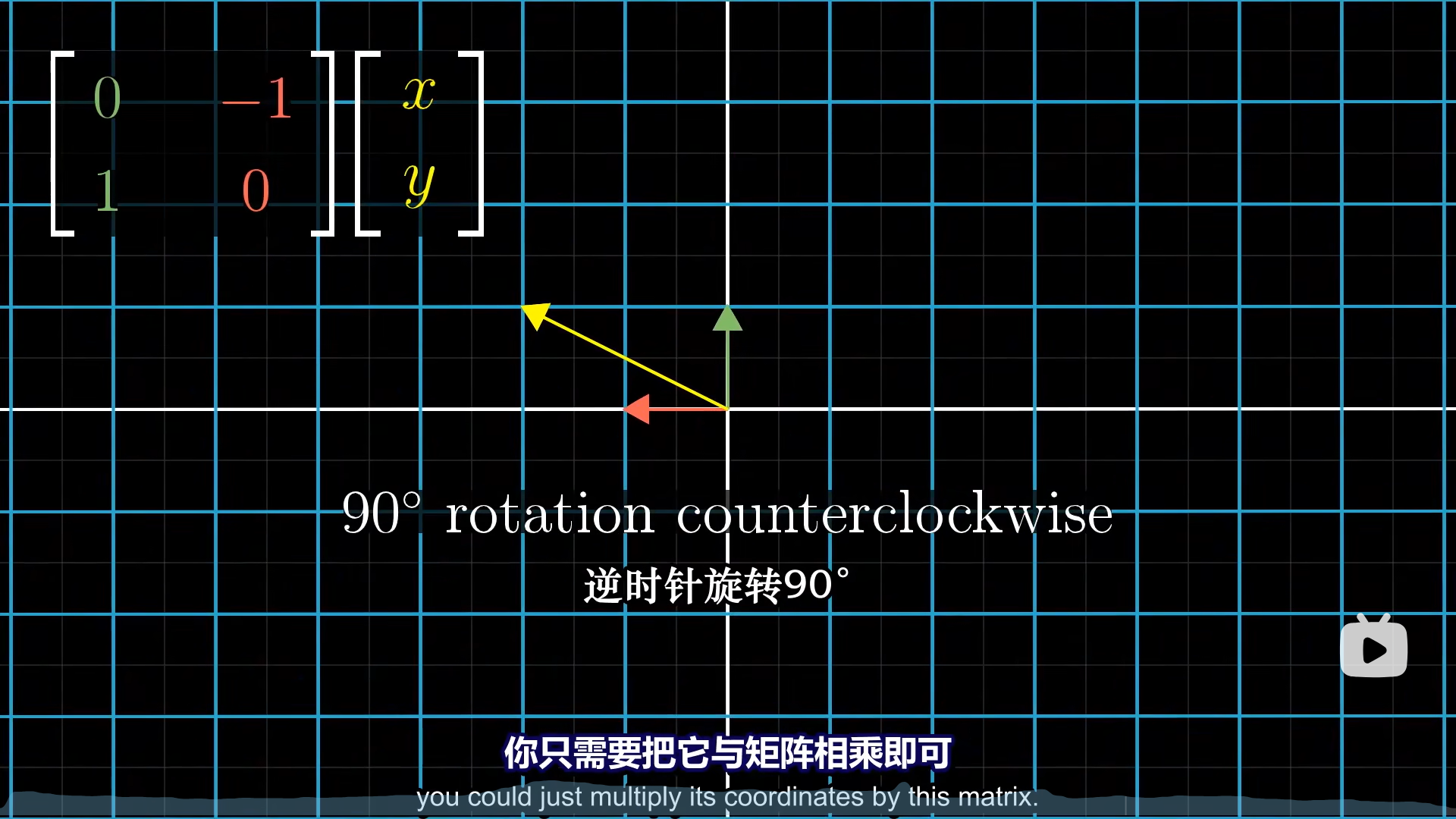
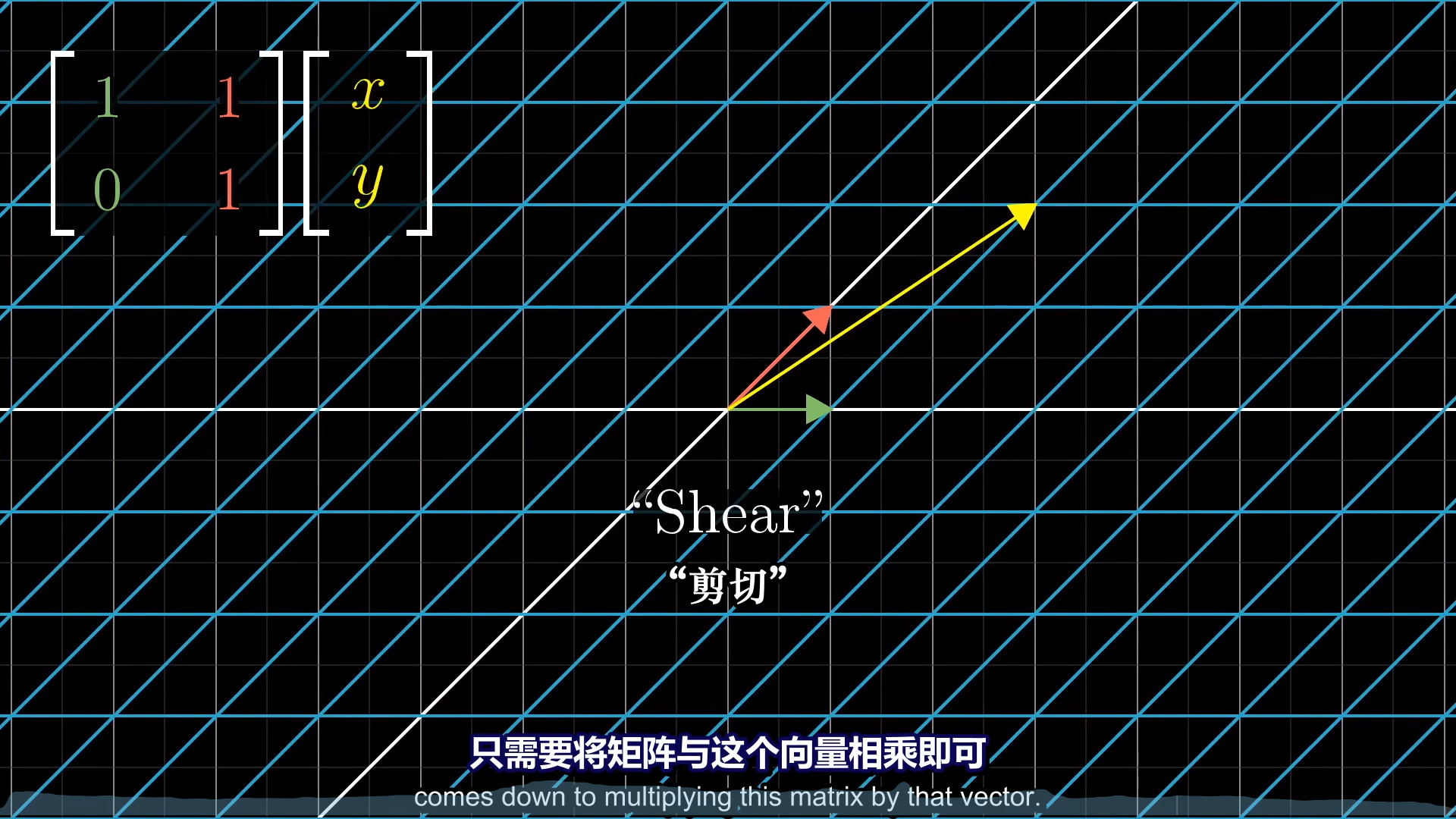
如果新的基底在一条直线上,那么原有的二维空间就会被挤压到一维空间上,这就是降维了。
进一步理解矩阵和矩阵相乘。
如果说一个矩阵描述了新基底,那么另一个矩阵就是把基底再进行一次变换,两次基底的变换可以复合成一次性的线性变换。
所以矩阵乘,有两种理解:
- 把一个空间的每一个向量都变成新的向量,形成新的空间
- 把两个线性变换复合为一个线性变换
按照这个思路去理解,只要不影响从右到左的变换顺序,那么就不影响最终结果,所以矩阵乘具有结合和分配,但是没有交换运算。

行列式
因为是线性变换,所以对于基底向量构成的方格的面积变换,这个比例对于任何方格都是一样的。
即使一个形状不是方格,也可以用方格近似,所以任意面积,在经过线性变换以后,变换的比例是恒定的。


这个面积变换的比例,就是行列式。
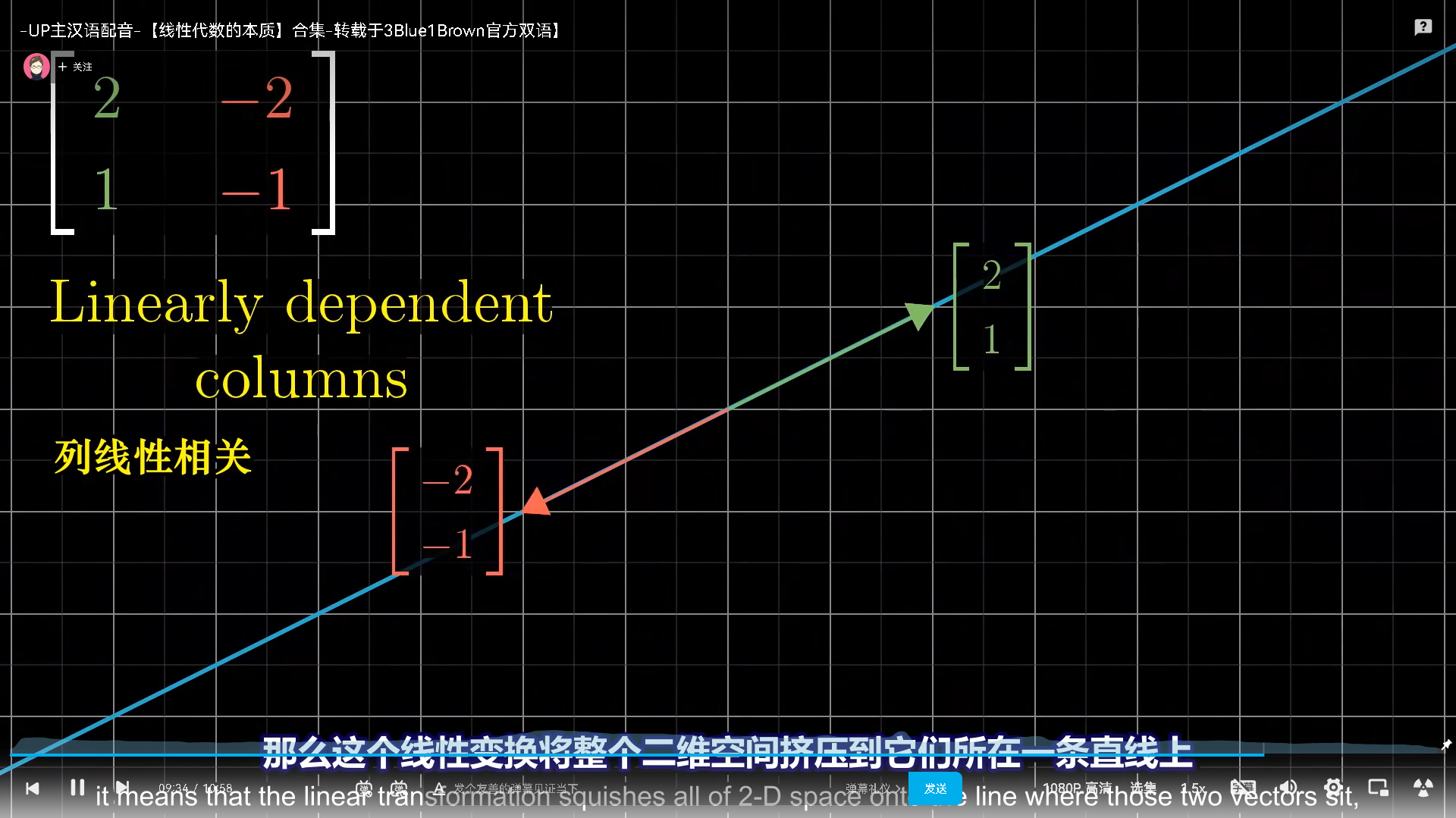
为什么存在线性相关向量的矩阵,行列式=0呢?就是因为降维了,导致体积被压缩为0.1
当然,行列式也是有可能出现负值的,那代表什么呢?对于二维空间来说就是翻了个面,学术点就是改变了空间的定向,所谓定向,就是基底的相对位置(比如二维中,正定向是i永远在j左边,三维中,符合右手定则)
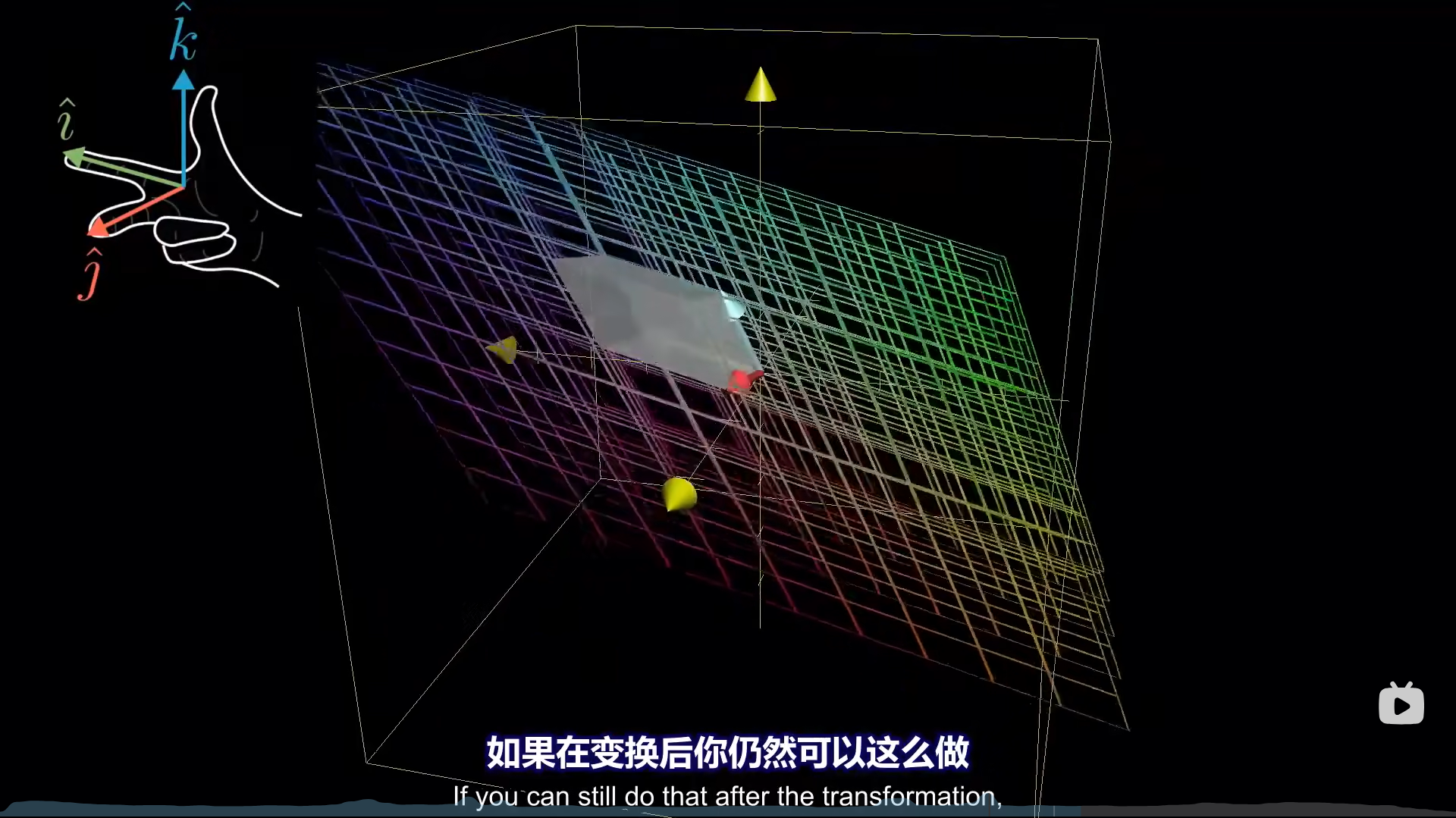
为什么把行列式的两行/两列交换后取值要加负号呢?就是因为交换会改变定向,相当于翻了个面。

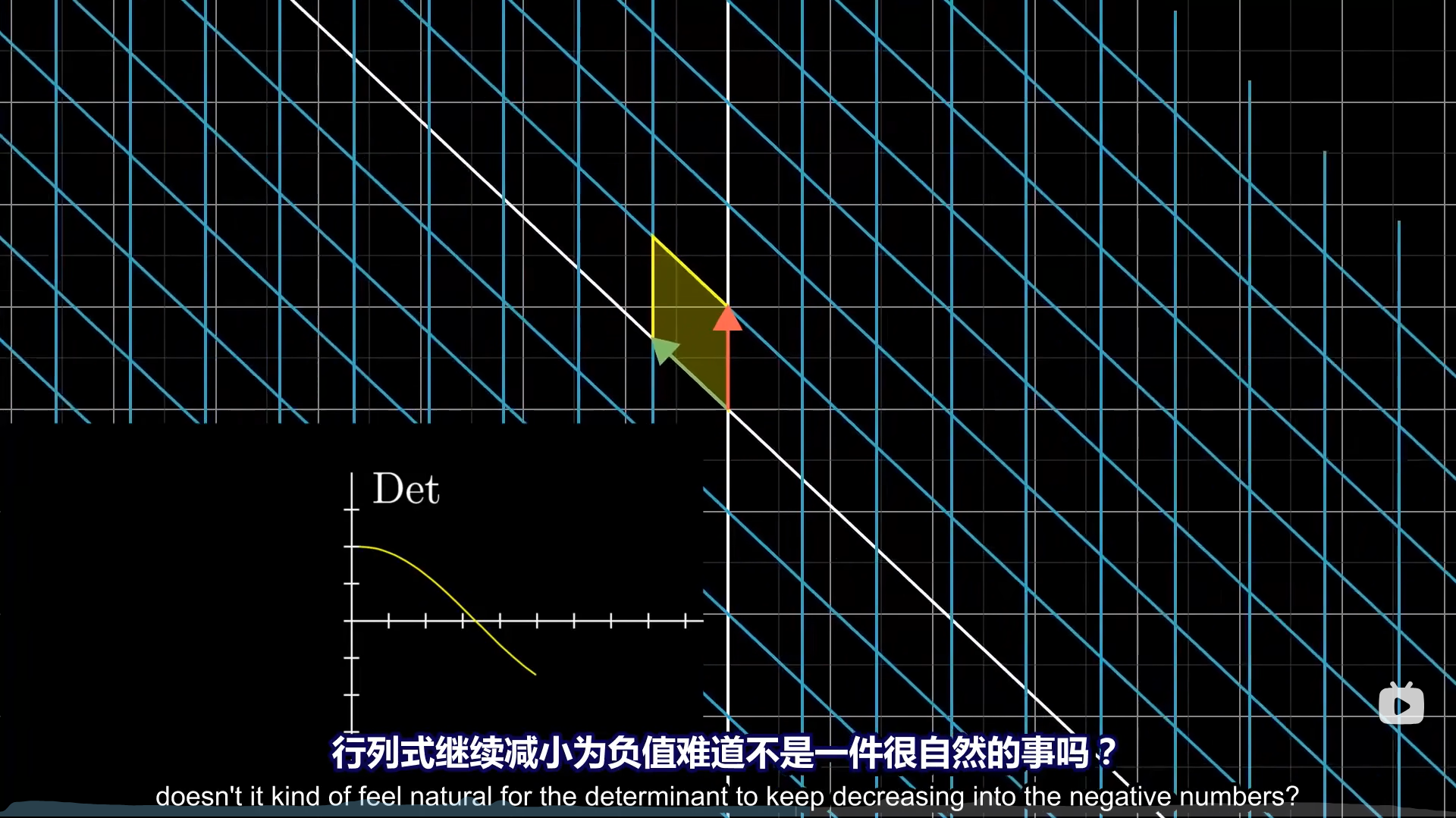
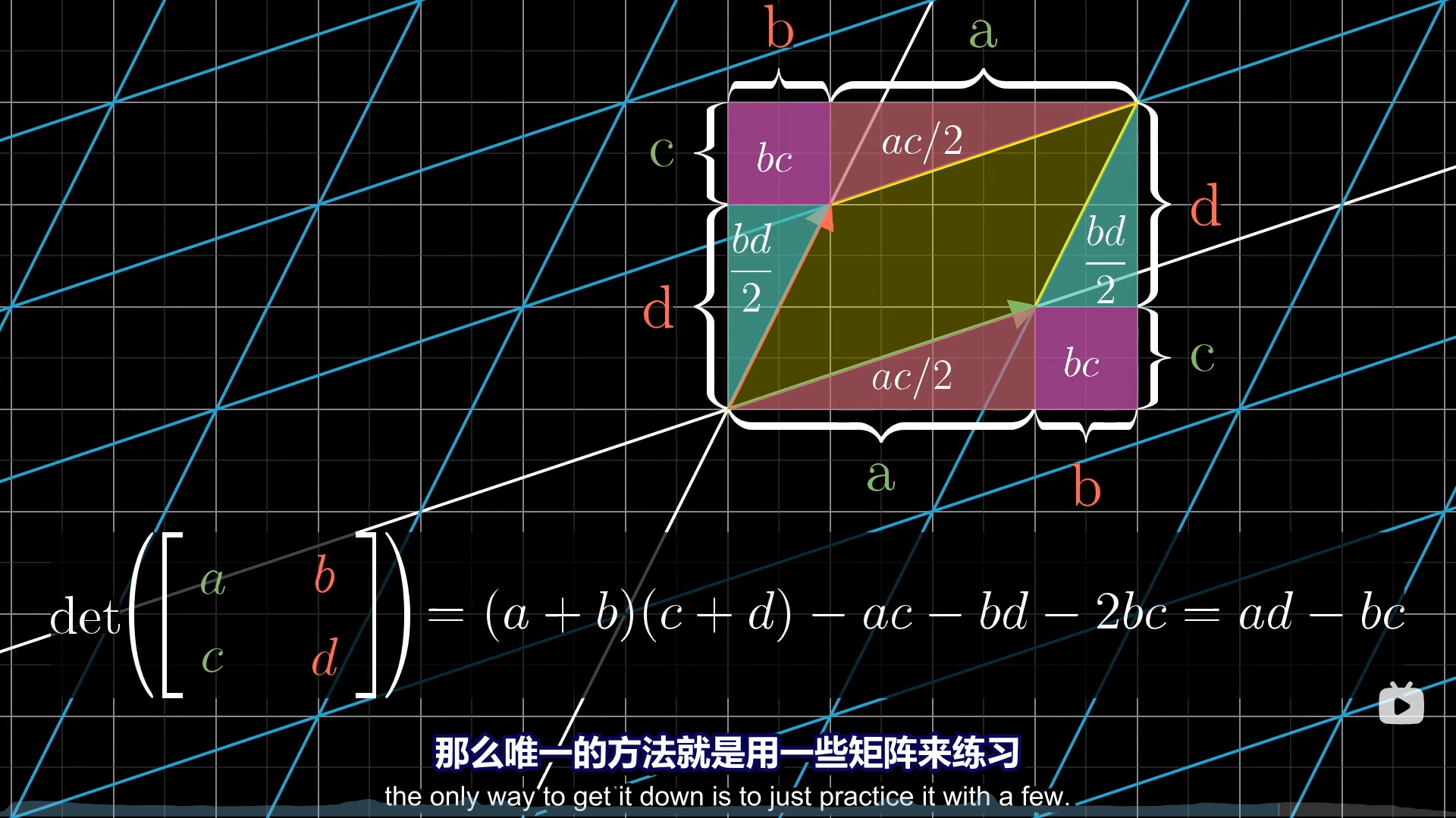
具体要问行列式怎么计算,下图是二维情况。当然,这就是图一乐,实际上你不会这么去算的,就是理解一下,确实是面积的放大比例。
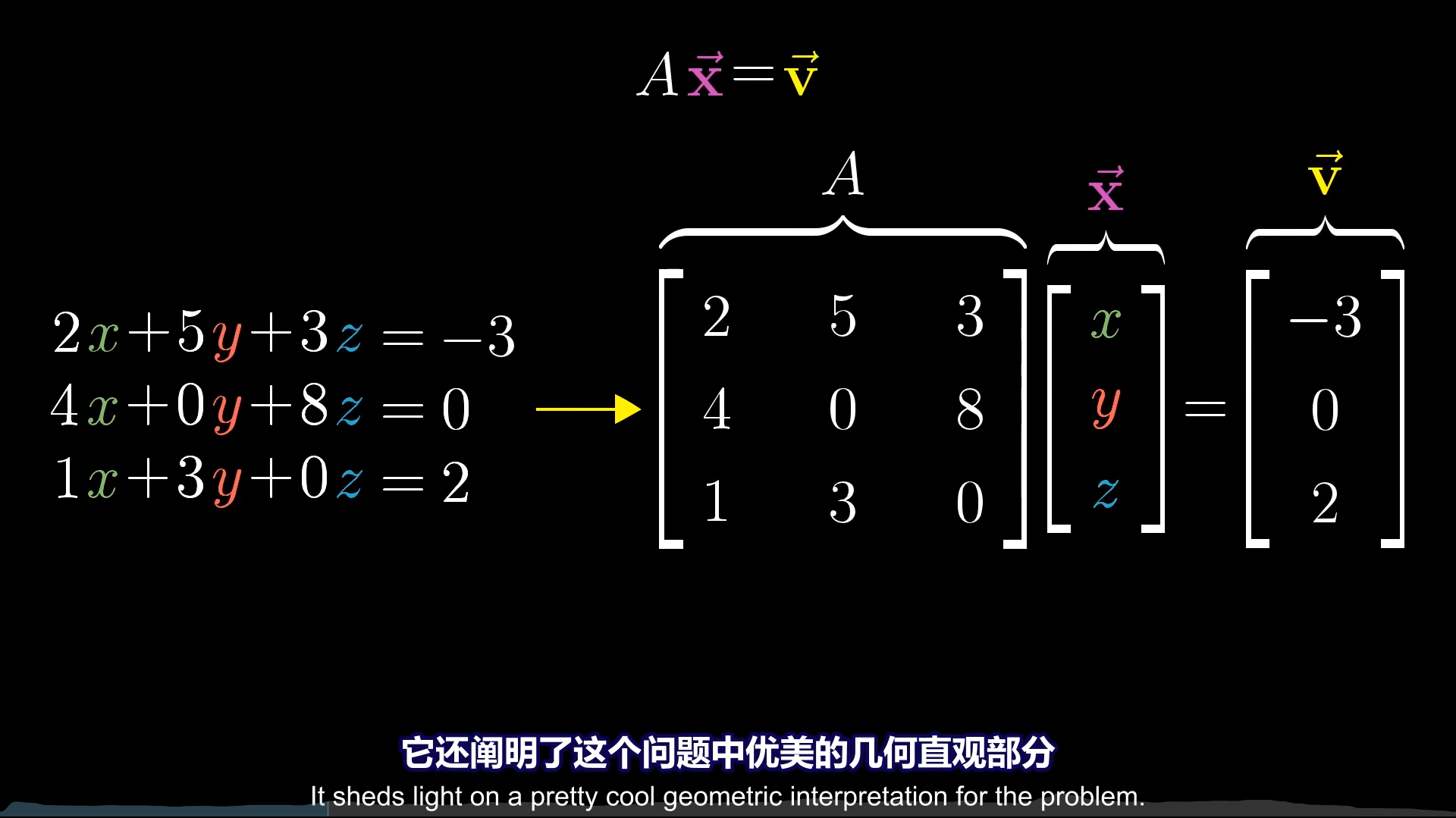
线性方程
我们先讨论非齐次线性方程。
其几何意义在于,寻找一个线性组合x,让这个向量经过基底A变换后,与v对齐
当然,这种情况是复杂的,线性变换后到底降没降维,可以用秩来描述。秩就是A张成的列空间的维度
如果r(A)<n,就代表降维了,自然det(A)=0
如果A的行列式不为0,也就是说A张成的空间可以把v覆盖,那么就有且只有一个x在变换后能和v重合。
这就是唯一解的条件:r(A)=n(或者行列式≠0),代表满秩,r(A,v)=r(A),代表A可以线性表出v。其实后一个条件压根没必要,只要满秩,A的空间维度一定可以覆盖v。
而且,因为是唯一解,具有一一映射的特性,所以可以通过逆映射,即一个逆向线性变换把v倒回x,这就是逆矩阵。
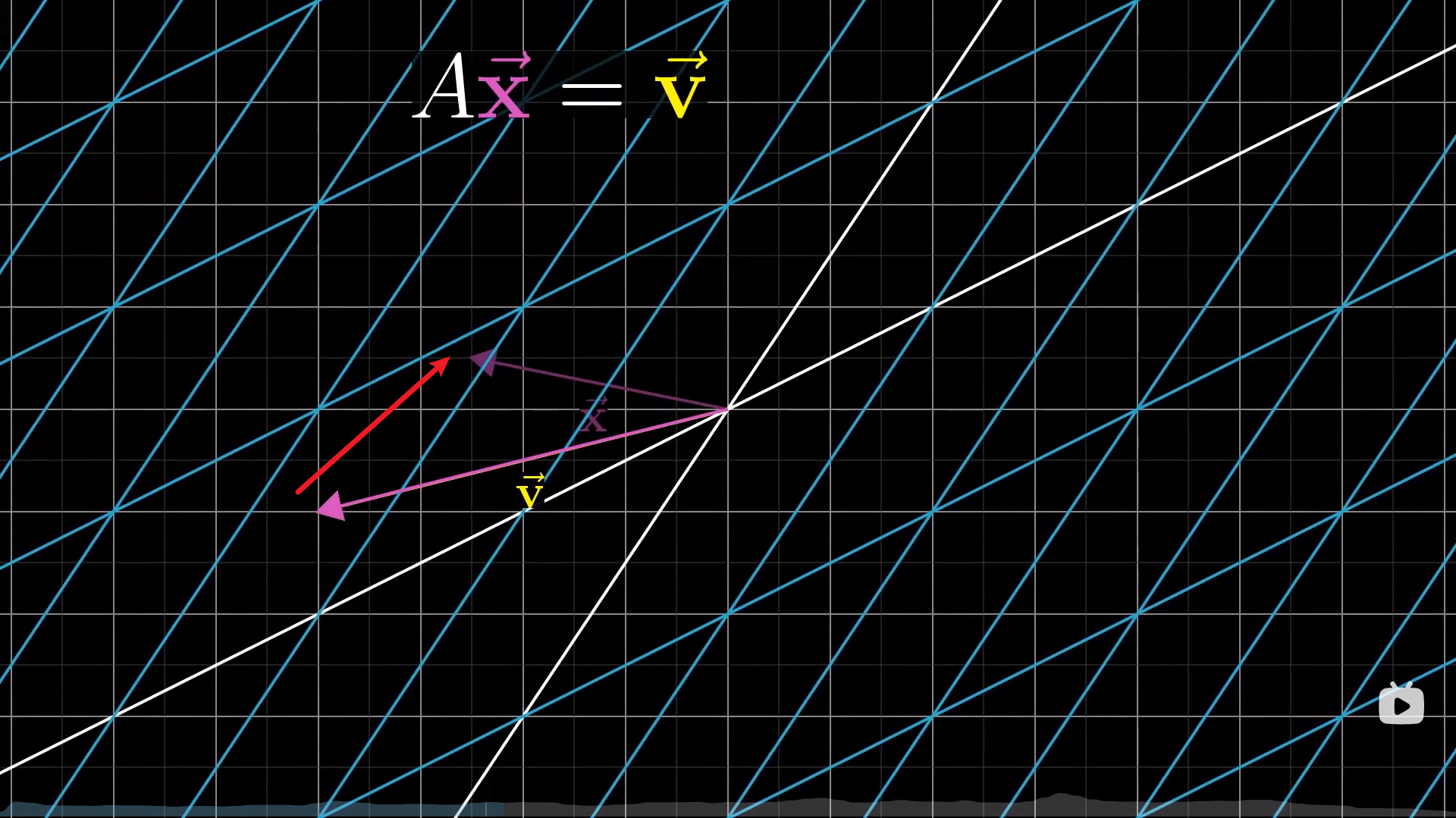
如果行列式=0,即r(A)< n,那么正向变换是降维的,也就是说会把空间压缩,但是你要知道,v是没有被压缩的,还是高维的,那么就有两种可能:
- v恰好落在降维后空间内,即v可以被A线性表出,即r(A)=r(A,b)
- v落在降维后空间外,即r(A)< r(A,b),此刻无解
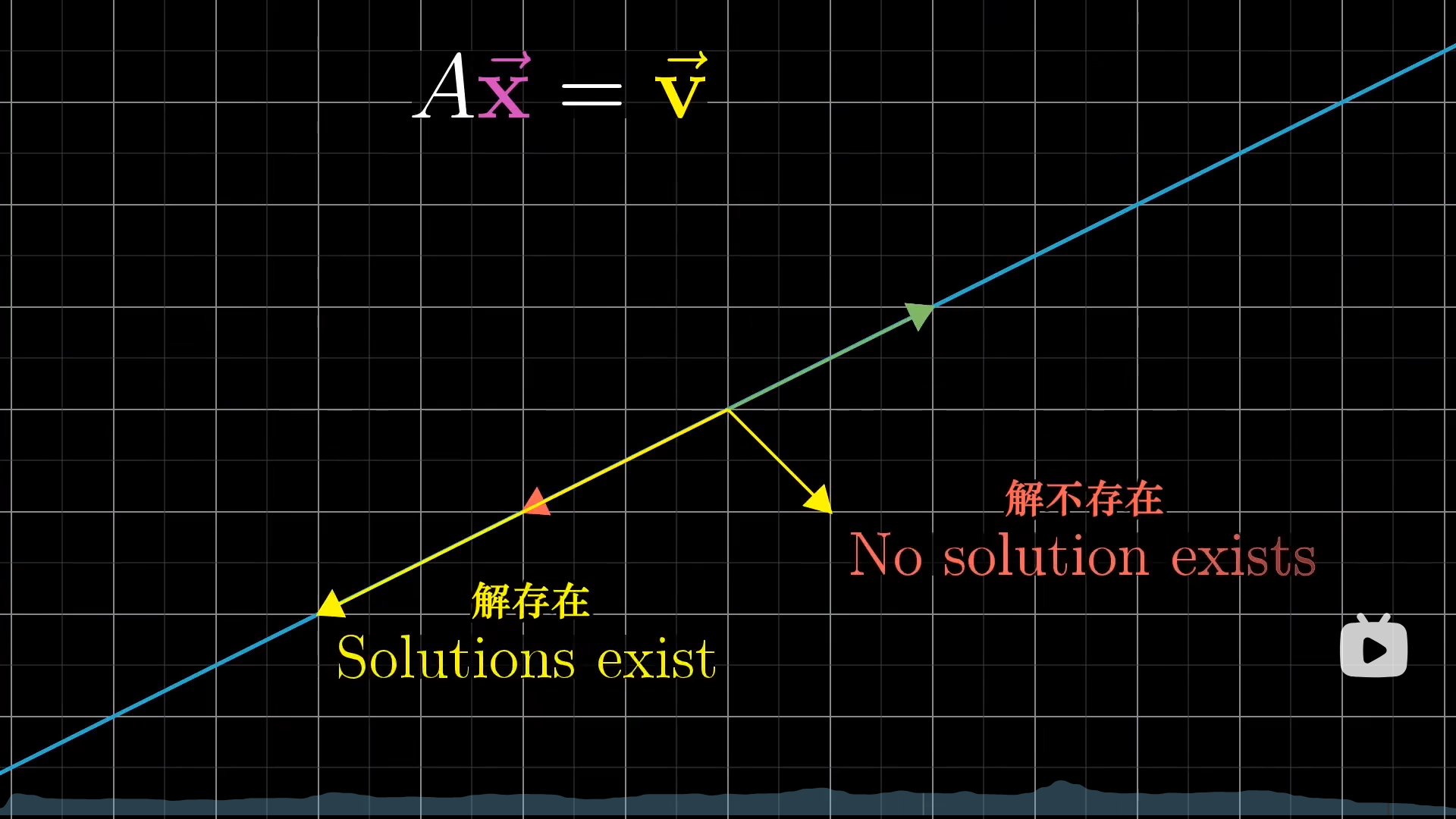
如果在降维后,还有解的话,那么v这个位置其实是被压缩了无数个向量的
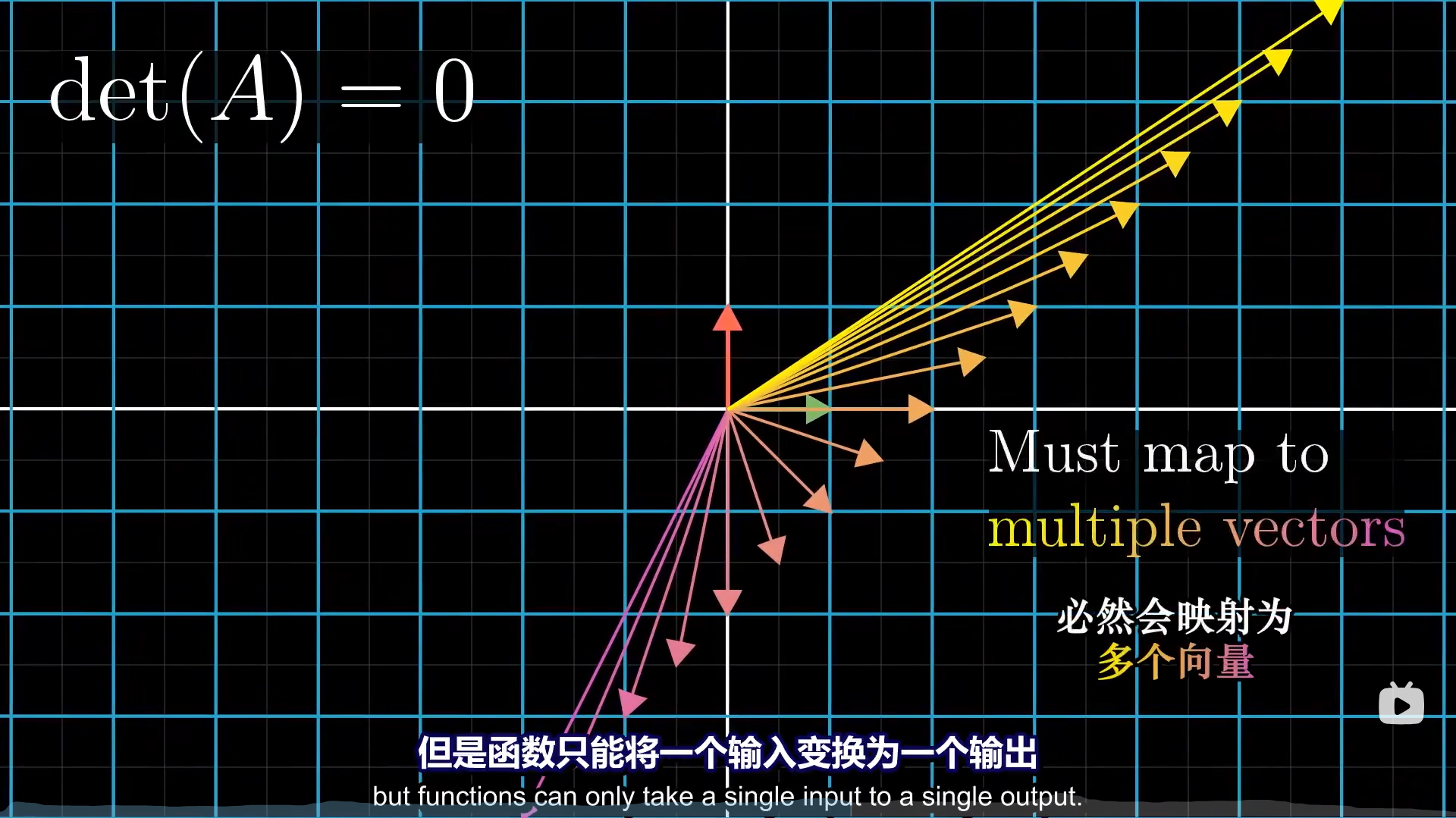
这不是一一映射,你自然无法把一条线逆向变回一个平面,所以det(A)=0时,没有逆矩阵。
从空间角度理解可逆变换的几何意义,就是不降维的变换。
非齐次说完了,说一下齐次吧。
其次就是v=0的特殊情况,0向量,无论被如何压缩,都可以落在空间之中,所以一定有解。
那么有一个解,还是无穷解,就取决于空间是否被压缩了,比如下面这条线被压缩为一个点的时候,无数个非零向量都被压缩为了0向量。
这就是齐次方程无穷非零解的情况,降维必无穷非零。
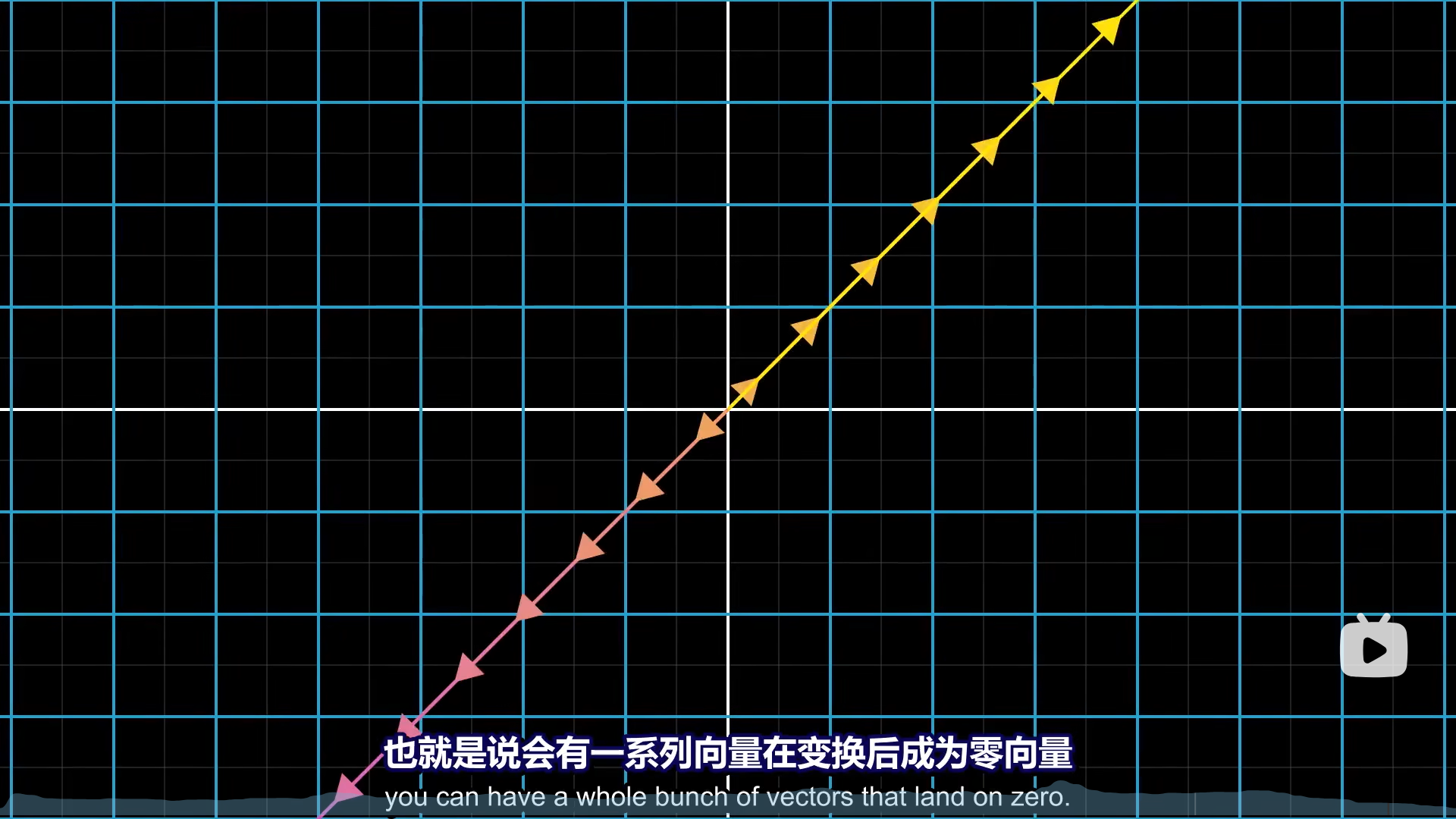
我们再来思考一下基础解系。你有想过为什么基础解系基底的数量是n-r(A)个吗?
以三维举例,如果只压缩1个维度,那么从空间上来说,就是沿着一条线把一个三维空间压扁。因此,只压缩一个维度,就会有一条线上的所有向量压缩为0向量,此时只需要1个基底就可以表示所有线性变换前的向量(解)
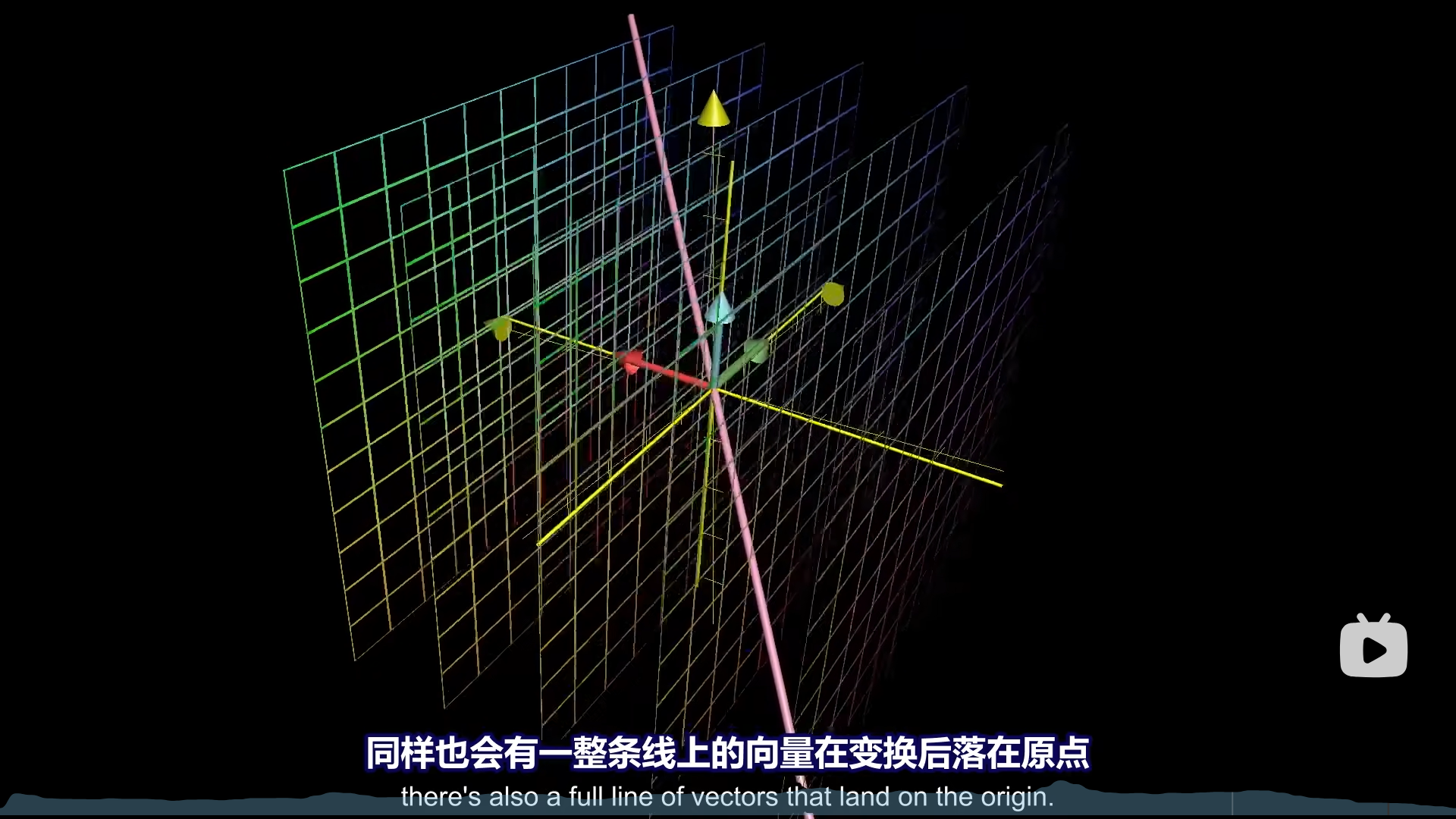

如果压缩2个维度呢?从空间来想象,就是沿着一个面的方向,把三维空间收缩成一束,想象一下你用拇指和食指套成一个圈儿,把很多线捏成一束的过程。
既然是沿着面,那么这整个面上的向量就都会被压缩为0向量,此时就需要用2个基底去表示这一个面上的解向量了。


最后,因为基础解系张成的子空间比较特殊,专门给起了个名字叫矩阵的“零空间”,或者“核”,还是比较形象的,压缩以后只剩一个点了,压缩前那不就是核心嘛。
基础解系就是零空间的基底。
非方阵
方阵代表同一个维度的空间之间的线性变换(不考虑降维情况)
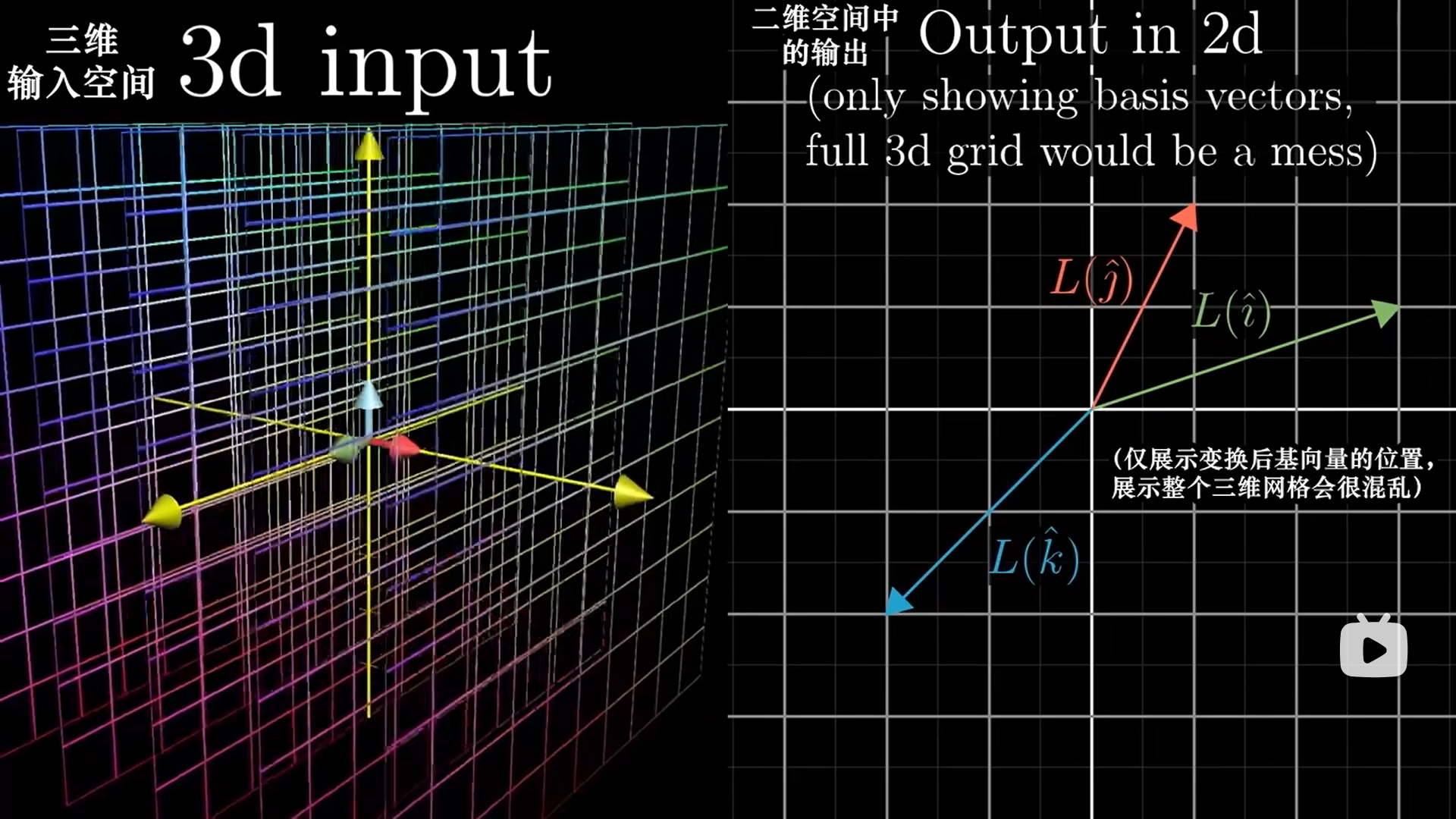
如果是非方阵,就要考虑m和n了。n列代表输入空间是n维的,m代表输出空间是m维的。
什么意思呢?比如在二维空间中,向量在一个平面上,经过了3×2矩阵,变成了3维向量后,向量存在于空间。
然而这并不代表这个升维后的向量,就能脱离原有的平面,非方阵只是把原有平面抬升到更高维的空间,但是平面还是平面,只是倾斜了,正如一张纸上的线,放到空间中,还是一条线。
说白了,m>n的情况下,矩阵只是把原来n个低维基底,转移到了高维的空间中,基底仍然是n个

如果是2×3矩阵呢?代表了把3维空间压缩到2维空间,这个变换是很不舒服的,因为把3个基底放到了2维空间,很明显有一个基底就是冗余的了。

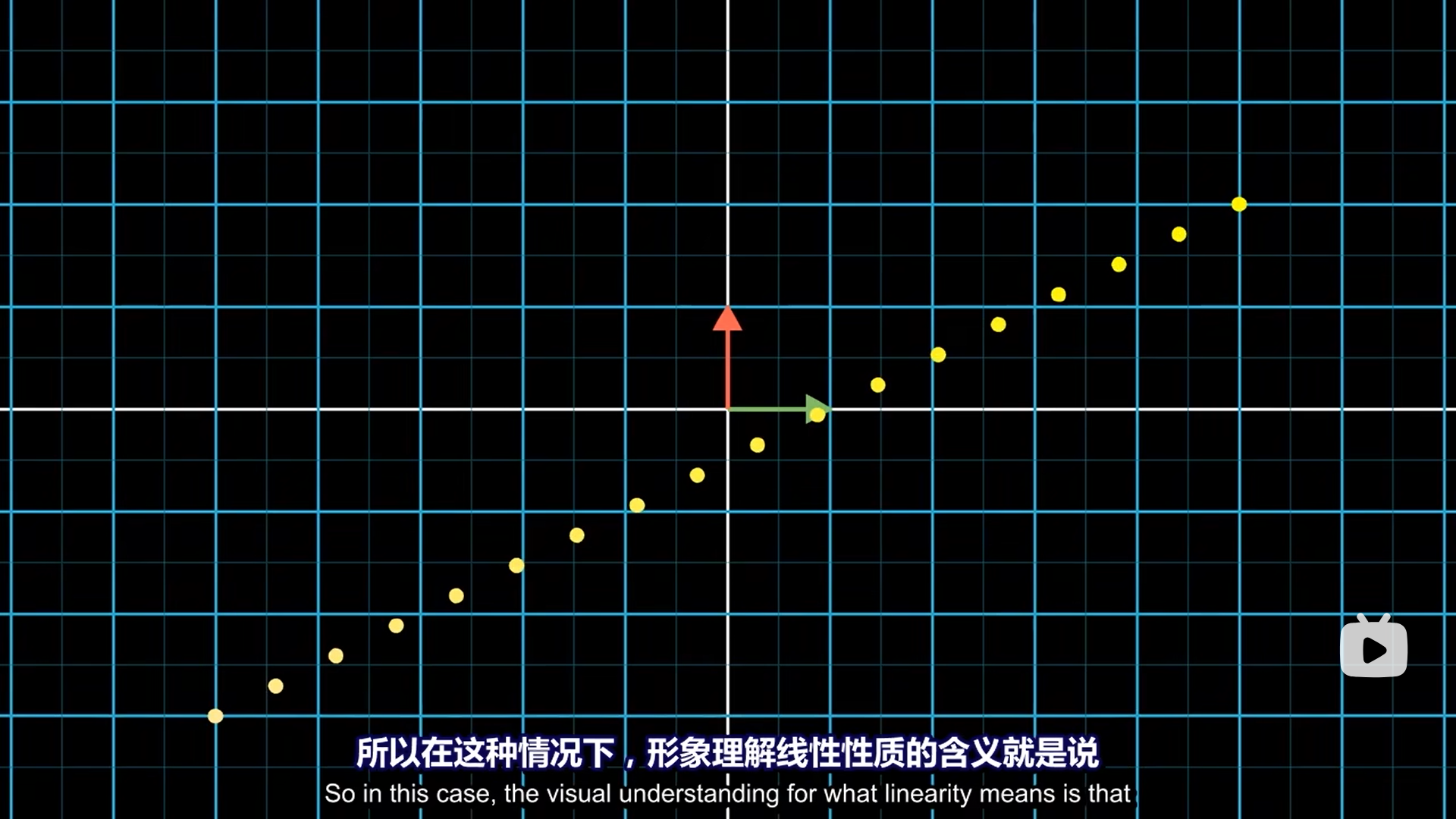
二维也可以压缩到一维,根据线性性质,平面上等距的点,压缩成数后,仍然等距。

点积
这一节比较难,我上来没听懂,关键在于那个对偶性,对偶性容易和对称混淆,其实完全没关系,要是我说的话,对偶性就是一种一一映射,是唯一的等价关系。
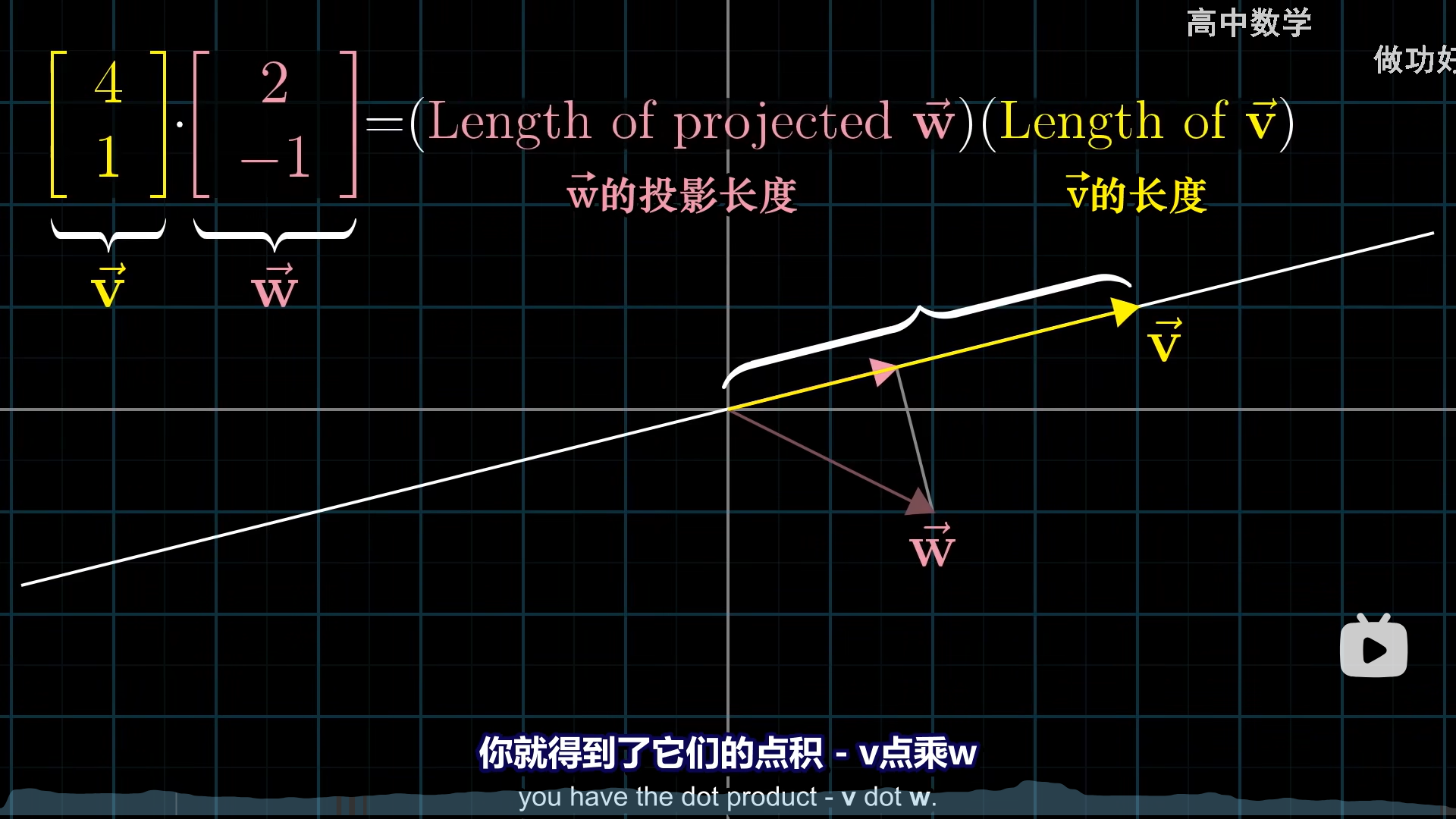
点积的计算公式是把对应的坐标相乘,并把结果相加。另一种计算方法是,把一个向量投影到另一个向量上,模之积就是点积。这两个计算方法看起来毫无关系,他们的联系是什么呢?
记住,我们的目标是发现点积,线性变换,投影的联系,现在讲引理。
我们前面说,线性变换可以把线性的空间变成线性的空间。
那么反过来,只要是把线性空间变成另一个线性空间,就一定有一个,且只有一个唯一的线性变换与之对应。
注意这个唯一性,即使是把二维空间压缩为数轴,不同的压缩方法,其放缩倍数都是不一样的,所以是新的线性空间对应唯一的线性变换。
引理说完了,先来寻找一下和单位向量点积是如何与投影联系起来的。
首先,投影是一个线性变换。把二维空间的向量,投影到一条直线上,很明显这是个线性过程,而且还是二维到一维的。
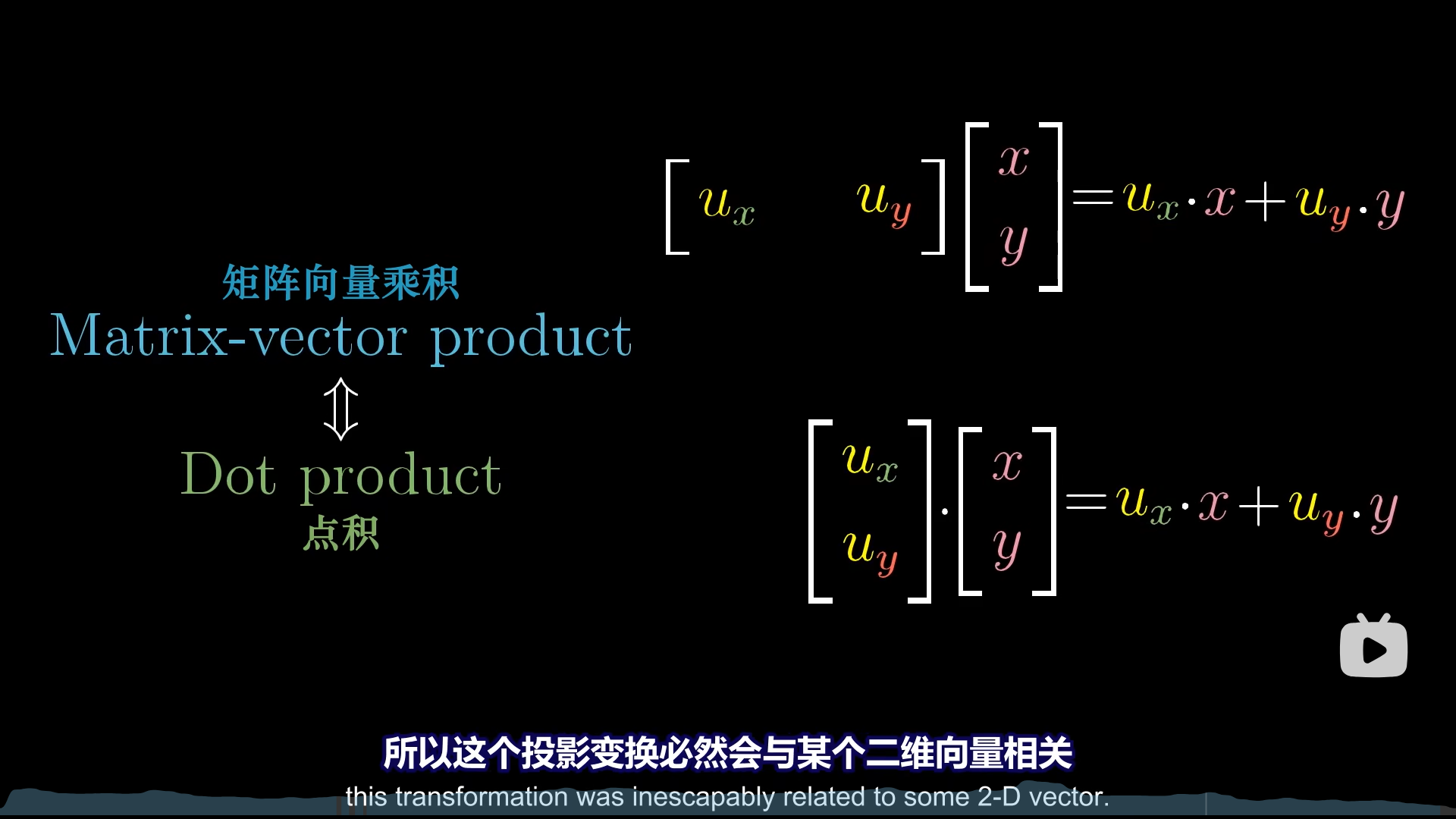
根据对偶性,只要是线性变换,就一定有一个1×2的矩阵与之对应,即投影矩阵。
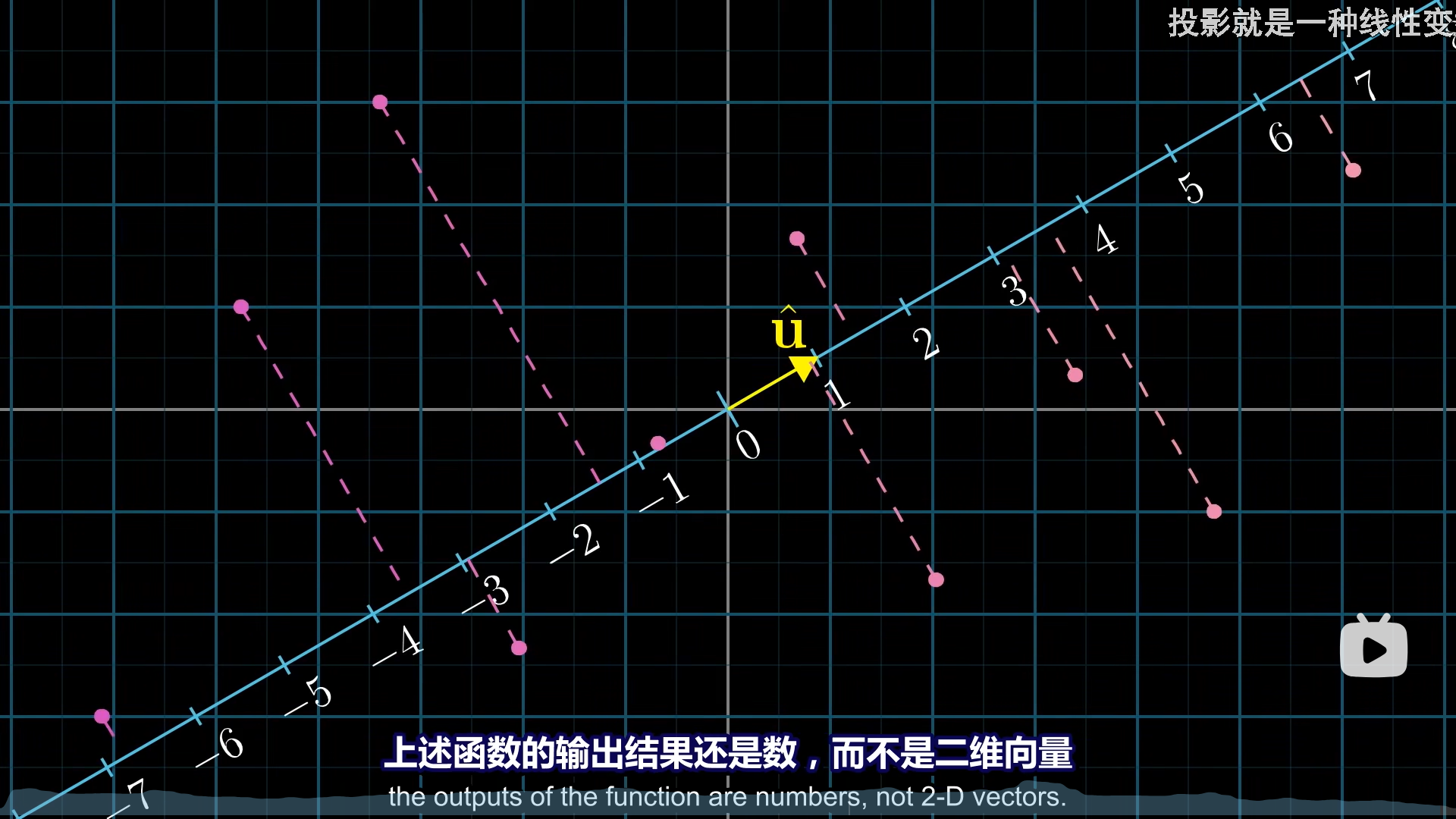
投影矩阵到底是多少呢?按照线性变换的几何意义,我们只需要找到i,j两个向量在目标直线上的位置,也就是他们的值就行。
此时引入一个单位向量 u ^ \hat{u} u^,根据对称性,i在直线上的投影值(新基底),恰好等于u的x轴
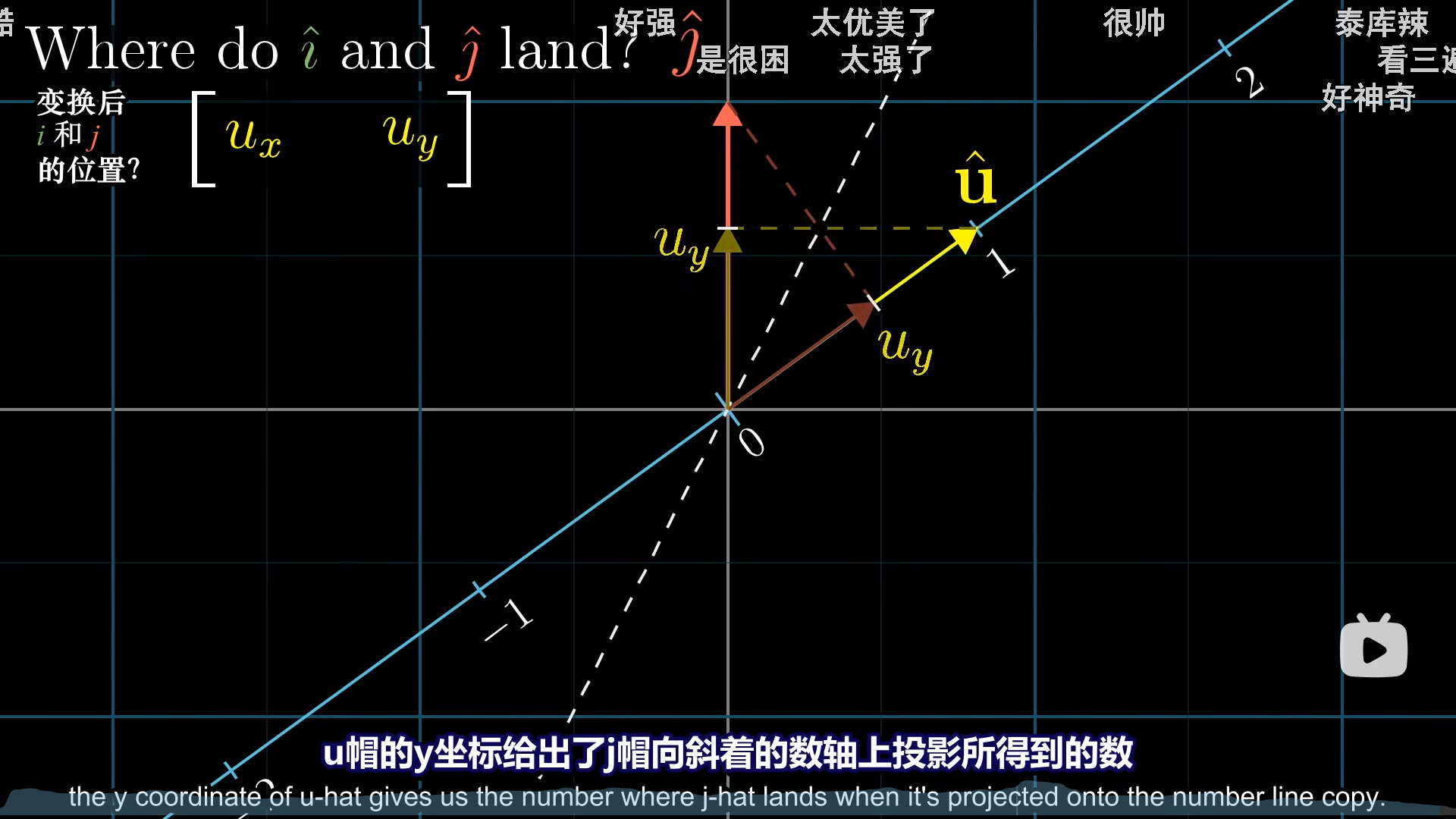
这样,我们就用线性变换表示出了投影运算,这是几何上的联系。
从数值上来看,向量通过投影矩阵进行线性变换,投影到单位向量所在直线上的值,恰好等于向量和单位向量的点积。
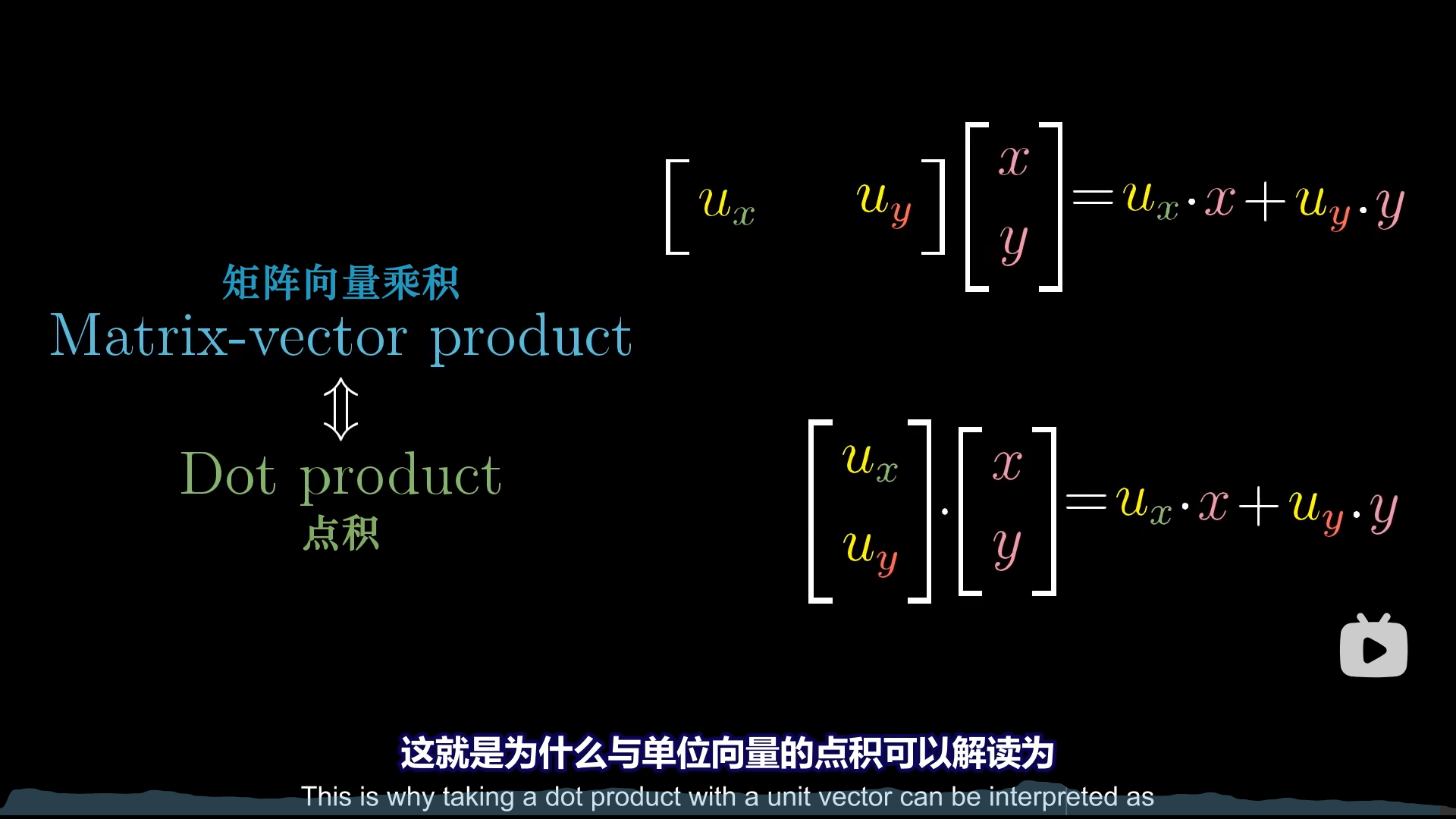
投影——(几何)——线性变换——(数值)——点积
整个对于单位向量,证明思路就是这样。
非单位向量呢?
非单位向量只是单位向量的放缩,计算点积的结果仍然是数,整个过程仍然是从二维到一维,所以仍然对应一个投影矩阵。
只不过因为投影后基底要放缩,所以投影矩阵整体是要比单位向量情况放缩k倍的,这个矩阵可以理解为先投影,再缩放(乘以向量的模)。
至于点积和线性变换,仍然是数值上的联系。如此,投影和点积就彻底联系起来了。
总的来说,这个证明过程用到了线性变换与矩阵的唯一对应性,也就是对偶性。
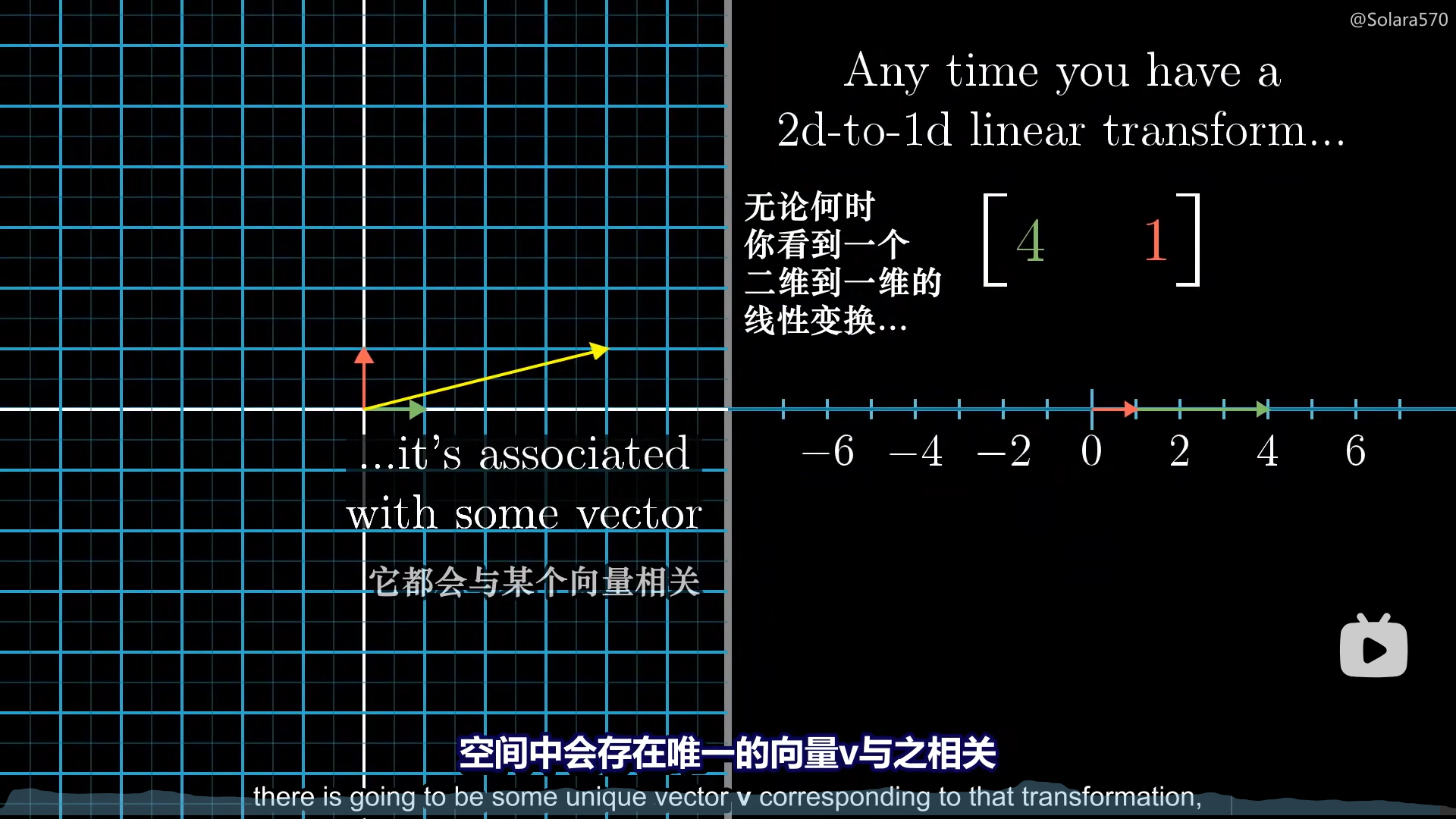
对于n维变1维的情况,必然有一个n×1的矩阵可以表示这个线性变换,把这个矩阵转置成向量,我们也可以说,任意一个n维变1维的线性变换,一定有一个空间中的向量v与之相关,这就是点积和线性变换的等价性。
叉积
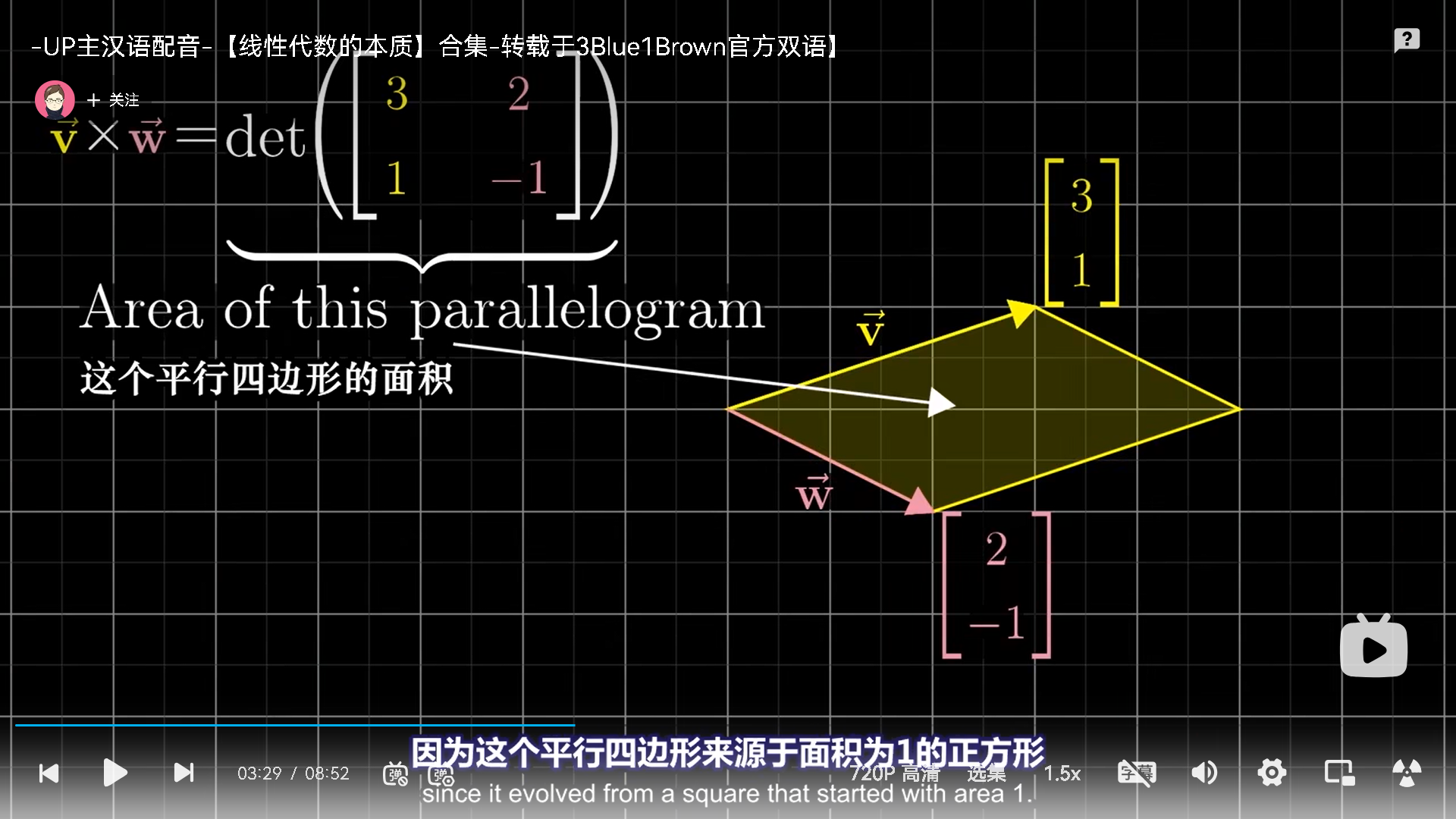
叉积结果的模,平行四边形的面积。
行列式的几何意义,恰好也是线性变换的放大倍数,就用叉积的两个向量当线性变换,计算行列式就等于叉积结果。
当然最后要定向,分正负。
实际上,叉积是一个向量,垂直于底面,模是底面积。叉积可以说是一个代表底面大小和方向的向量。

具体如何计算叉积呢?就是用行列式, 好啦,问题来了,行列式怎么和叉积的几何意义联系起来的呢?还是对偶性。

一个线性变换,可以等价于和对偶向量的点乘。

整体的计划如下:
- 首先通过v和w构造线性变换
- 然后求出对偶向量,这个对偶向量恰好就是叉积
- 而且这个求对偶向量的过程,恰好也就是通过行列式计算叉积的过程。

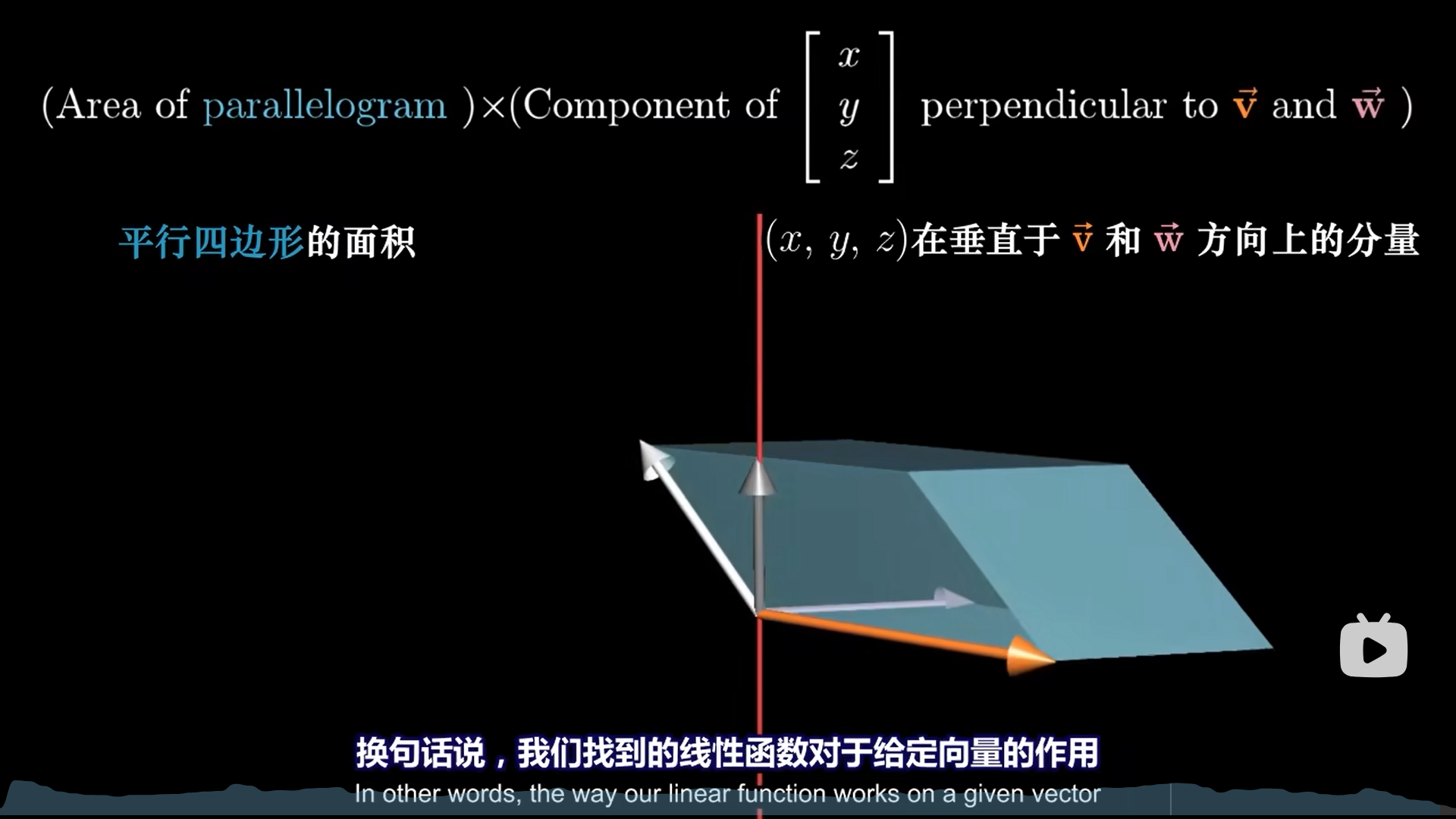
这是一个输入向量,输出值的函数,行列式计算结果代表平行六面体的体积,很明显这是个线性变换(行列式的特点就是这样)。
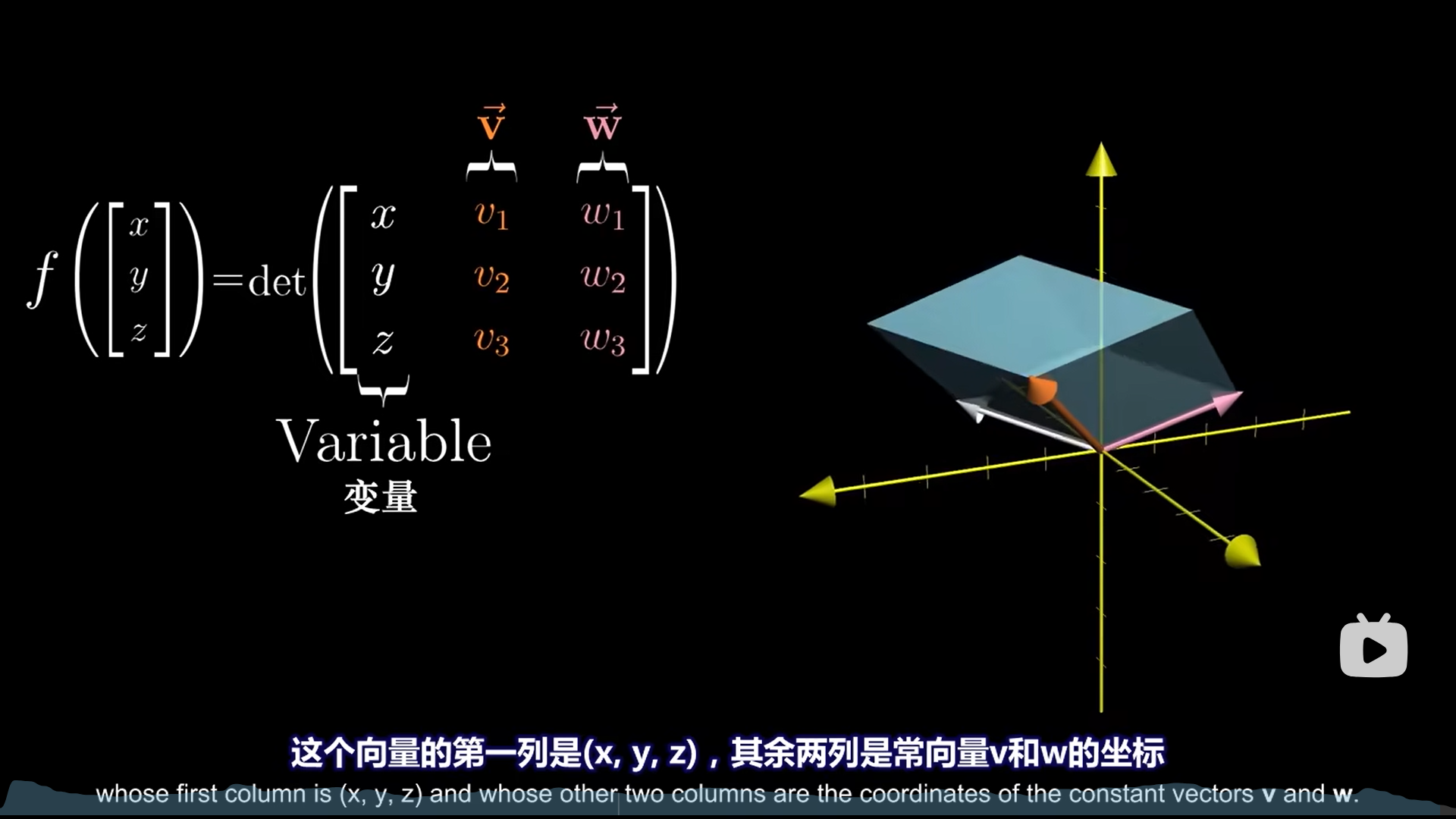
根据对偶性,自然有一个1×3的线性变换,进而根据可以变成和3维向量点积,这个三维向量恰好就是我们要的点积。
之所以叉积要用ijk去代替xyz,写成行列式的样子,其实原理就在于此,ijk只是告诉你,算完以后的p是一个向量。

我们到这里只是给出了p的公式,还没有解释为啥p的模就等于底面积。
还得从最开始,平行六面体的体积来看。设(x,y,z)向量为a。则V=底面积×高=a在p上的投影×p的模
你要注意,高=a在p上的投影,所以底面积就自然等于p的模了。