二叉搜索树的(查找、插入、删除)

news2024/11/25 22:27:42

一、二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

1、若它的左子树不为空，则左子树上所有节点的值都小于根节点的值；

2、若它的右子树不为空，则右子树上所有节点的值都大于根节点的值；

3、它的左右子树也分别为二叉搜索树

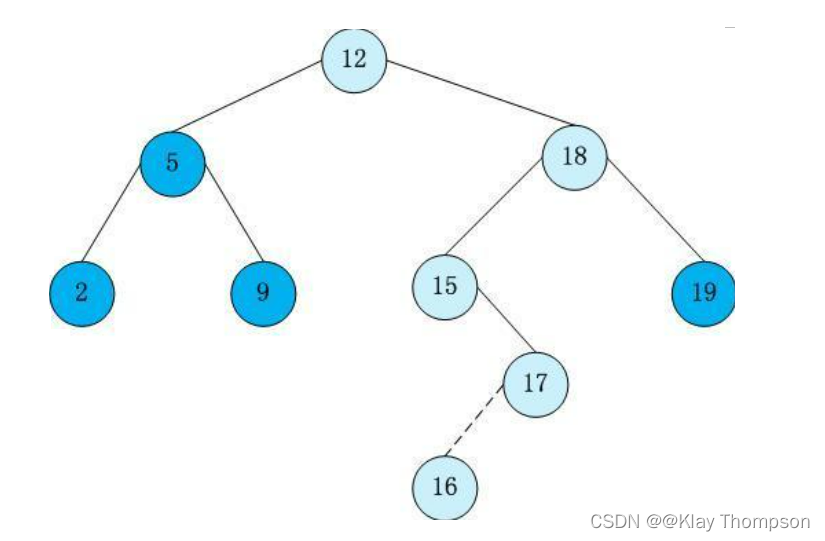
下图就是一个二叉搜索树：

二、二叉树的定义

template<class K>
struct BSTreeNode
{
	BSTreeNode<K>* _right;
	BSTreeNode<K>* _left;
	K _key;

	BSTreeNode(const K& key = K())
		:_right(nullptr)
		,_left(nullptr)
		,_key(key)
	{
	}
};

template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
    bool find(const K& key){}//查找
    bool insert(const K& key){}//插入 
	bool erase(const K& key){}//删除
private：
    Node* _root;
};

三、二叉搜索树的查找节点

非递归写法：

如果root为空，那么查找失败，没有要查找的节点；如果root不为空，比较root->key和要查找的值，如果要查找的值大于root->key，就到右子树接着找，反之，到左子树接着找。找到返回true，没有找到返回false。

    bool find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
		return false;
	}

递归写法：

查找思想还是和非递归一样的，如果root为空，返回false，如果root->key大于要找的值，那么递归到左子树去找（转换成一个子问题），反之，递归到右子树去找。

    
    bool findR(const K& key)
	{
		return _findR(_root, key);
	}


    bool _findR(Node* root, const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key == key)
		{
			return true;
		}
		else if(root->_key < key)
		{
			return _findR(root->_right, key);
		}
		else
		{
			return _findR(root->_left, key);
		}
	}

四、二叉搜索树的插入节点

非递归写法：

要插入一个数据，首先得找到插入的位置，所以插入分为两大步：

1、找到要插入的位置

如果树中存在一个节点的key与要插入的数相同，则不会插入。找位置的时候要同时有一个指针记录父节点，走到空就结束

2、插入数据

判断插入的数据比父节点大还是小，如果小则插在左边，反之则插在右边

    bool insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
		}
		else
		{
			Node* cur = _root;
			Node* parent = cur;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}
			if (key > parent->_key)
			{
				parent->_right = new Node(key);
			}
			else
			{
				parent->_left = new Node(key);
			}
		}
		return true;
	}

递归写法：

    bool insertR(const K& key)
	{
		return _insertR(_root, key);
	}

    //这里要传引用，我们就不需要找父节点了
    bool _insertR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			root = new Node(key);
			return true;
		}

		if (root->_key < key)
		{
			return _insertR(root->_right, key);
		}

		else if (root->_key > key)
		{
			return _insertR(root->_left, key);
		}

		else
		{
			return false;
		}
	}

五、二叉搜索树的删除节点

删除节点大致可分为三种情况：

1、要删除节点左右都为空；

2、要删除节点左为空或右为空；

3、要删除节点左右都不为空。

第一点和第二点又可以看成一点。

要注意特殊情况：要删除的节点是根节点。

非递归写法：

    bool erase(const K& key)
	{
		Node* cur = _root;
		Node* parent = cur;
		while (cur)
		{
			if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			//找到要被删的节点了
			else
			{
				//1、要删除的这个节点是叶子节点或度为1（可直接删除）
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (parent->_right == cur)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}
					}
				}
				else if(cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (parent->_right = cur)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}
					}
				}
				//2、要删除的这个节点度为2（替换法）
				else
				{
					//找左树中的最大值或右树中的最小值与被删节点交换，再删除
					//找左树中的最大值
					Node* leftMax = cur->_left;
					Node* PLeftMax = cur;
					while (leftMax->_right)
					{
						PLeftMax = leftMax;
						leftMax = leftMax->_right;
					}
					
					swap(cur->_key, leftMax->_key);//交换值
					//删除leftMax
					if (PLeftMax->_right == leftMax)
					{
						if (leftMax->_right == nullptr)
						{
							PLeftMax->_right = leftMax->_left;
						}
						else
						{
							PLeftMax->_right = leftMax->_right;
						}
					}
					if (PLeftMax->_left == leftMax)
					{
						if (leftMax->_right == nullptr)
						{
							PLeftMax->_left = leftMax->_left;
						}
						else
						{
							PLeftMax->_left = leftMax->_right;
						}
					}
					cur = leftMax;
				}
				delete cur;
				return true;
			}
		}
		return false;
	}

递归写法：

    bool eraseR(const K& key)
	{
		return _eraseR(_root, key);
	}

    bool _eraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key < key)
		{
			return _eraseR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _eraseR(root->_left, key);
		}
		else
		{
			Node* del = root;
			//找到了被删除节点
			//1、左为空或右为空或左右都为空
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			}
			//2、左右都不为空
			else
			{
				//左树找最大值
				Node* LeftMax = root->_left;
				while (LeftMax->_right)
				{
					LeftMax = LeftMax->_right;
				}
				swap(root->_key, LeftMax->_key);
				

				//删除LeftMax节点
				return _eraseR(root->_left, key);
			}
			delete del;
			return true;
		}
	}

六、二叉搜索树的应用

1、K模型（也就是我们后面学是set）：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。

2、KV模型（也就是我们后面学是map）：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。

七、二叉搜索树的实现

template<class K>
struct BSTreeNode
{
	BSTreeNode<K>* _right;
	BSTreeNode<K>* _left;
	K _key;

	BSTreeNode(const K& key = K())
		:_right(nullptr)
		,_left(nullptr)
		,_key(key)
	{
	}
};

template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	BSTree()
		:_root(nullptr)
	{}

	BSTree(const BSTree<K>& tree)
	{
		_root = Copy(tree._root);
	}

	BSTree<K>& operator=(BSTree<K> tmp)
	{
		swap(_root, tmp._root);
		return *this;
	}

	~BSTree()
	{
		Destory(_root);
	}

	bool insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
		}
		else
		{
			Node* cur = _root;
			Node* parent = cur;
			while (cur)
			{
				if (key > cur->_key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}
			if (key > parent->_key)
			{
				parent->_right = new Node(key);
			}
			else
			{
				parent->_left = new Node(key);
			}
		}
		return true;
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	

	bool find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (key > cur->_key)
			{
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
		return false;
	}

	bool erase(const K& key)
	{
		Node* cur = _root;
		Node* parent = cur;
		while (cur)
		{
			if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			//找到要被删的节点了
			else
			{
				//1、要删除的这个节点是叶子节点或度为1（可直接删除）
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (parent->_right == cur)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}
					}
				}
				else if(cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (parent->_right = cur)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}
					}
				}
				//2、要删除的这个节点度为2（替换法）
				else
				{
					//找左树中的最大值或右树中的最小值与被删节点交换，再删除
					//找左树中的最大值
					Node* leftMax = cur->_left;
					Node* PLeftMax = cur;
					while (leftMax->_right)
					{
						PLeftMax = leftMax;
						leftMax = leftMax->_right;
					}
					
					swap(cur->_key, leftMax->_key);//交换值
					//删除leftMax
					if (PLeftMax->_right == leftMax)
					{
						if (leftMax->_right == nullptr)
						{
							PLeftMax->_right = leftMax->_left;
						}
						else
						{
							PLeftMax->_right = leftMax->_right;
						}
					}
					if (PLeftMax->_left == leftMax)
					{
						if (leftMax->_right == nullptr)
						{
							PLeftMax->_left = leftMax->_left;
						}
						else
						{
							PLeftMax->_left = leftMax->_right;
						}
					}
					cur = leftMax;
				}
				delete cur;
				return true;
			}
		}
		return false;
	}

	//-----------------------------------递归写法---------------------------------------
	bool findR(const K& key)
	{
		return _findR(_root, key);
	}

	bool insertR(const K& key)
	{
		return _insertR(_root, key);
	}

	bool eraseR(const K& key)
	{
		return _eraseR(_root, key);
	}

private:
	bool _eraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key < key)
		{
			return _eraseR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _eraseR(root->_left, key);
		}
		else
		{
			Node* del = root;
			//找到了被删除节点
			//1、左为空或右为空或左右都为空
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			}
			//2、左右都不为空
			else
			{
				//左树找最大值
				Node* LeftMax = root->_left;
				while (LeftMax->_right)
				{
					LeftMax = LeftMax->_right;
				}
				swap(root->_key, LeftMax->_key);
				

				//删除LeftMax节点
				return _eraseR(root->_left, key);
			}
			delete del;
			return true;
		}
	}

	Node* Copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;
		Node* Croot = new Node(root->_key);
		Croot->_left = Copy(root->_left);
		Croot->_right = Copy(root->_right);
		return Croot;
	}

	void Destory(Node*& root)
	{
		if (root == nullptr)
		{
			return;
		}
		/*if (root->_left == nullptr && root->_right == nullptr)
		{
			delete root;
			root = nullptr;
			return;
		}*/
		Destory(root->_left);
		Destory(root->_right);
		delete root;
		root = nullptr;
	}

	bool _insertR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			root = new Node(key);
			return true;
		}
		if (root->_key < key)
		{
			return _insertR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _insertR(root->_left, key);
		}
		else
		{
			return false;
		}
	}


	bool _findR(Node* root, const K& key)
	{
		if (root == nullptr)
			return false;
		if (root->_key == key)
		{
			return true;
		}
		else if(root->_key < key)
		{
			return _findR(root->_right, key);
		}
		else
		{
			return _findR(root->_left, key);
		}
	}

	void _InOrder(Node* root)
	{
		//中序
		if (root == nullptr)
		{
			return;
		}
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}

private:
	Node* _root;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/912647.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

使用rook搭建Ceph集群

使用rook搭建Ceph集群

宿主机&#xff1a; MacBook Pro&#xff08;Apple M2 Max&#xff09; VMware Fusion Player 版本 13.0.2 VM软硬件&#xff1a; ubuntu 22.04.2 4核 CPU&#xff0c;5G 内存&#xff0c;40G硬盘 *每台机器分配硬件资源很重要&#xff0c;可以适当超过宿主机的资源量&am…
阅读更多...
张驰咨询：有效导入精益生产咨询，企业提升竞争力的关键

张驰咨询：有效导入精益生产咨询，企业提升竞争力的关键

精益生产是一种源于日本的先进生产管理理念&#xff0c;旨在通过消除生产过程中的浪费&#xff0c;提高生产效率和质量&#xff0c;降低成本&#xff0c;从而提升企业的竞争力。在我国&#xff0c;越来越多的企业开始尝试导入精益生产咨询&#xff0c;但效果并不尽如人意。为了…
阅读更多...
关于slot-scope已经废弃的问题

关于slot-scope已经废弃的问题

说起来啊&#xff0c;这个问题啊&#xff0c;我之前一直没关注&#xff0c;还是webstorm给我的警告。 因为使用了element-ui的组件库&#xff0c;所以在使用组件的时候往往就cv大法了&#xff0c;直到今天用webstorm写代码是&#xff0c;提示了如下的错误 我这一看&#xff0c…
阅读更多...
伦敦金短线好还是长线好

伦敦金短线好还是长线好

在伦敦金投之中&#xff0c;长期有一个争论很久的问题&#xff0c;那就是伦敦金投资究竟是长线好还是短线好&#xff1f;不同的投资者对这个问题有不同的看法&#xff0c;一般认为&#xff0c;伦敦金投资比较适合短线交易。笔者也将讨论这个问题&#xff0c;看看伦敦金投资是不…
阅读更多...
《网络是怎样连接的》（四）

《网络是怎样连接的》（四）

本文主要取材于 《网络是怎样连接的》 第四章。 目录 4.1 互联网的基本结构 4.2光纤接入网&#xff08;FTTH&#xff09; 4.3 接入网中使用的PPP和隧道 4.4 网络运营商的内部 4.5 跨越运营商的网络包 简述&#xff1a;本文主要内容是解释 网络包是如何通过互联网接入路由…
阅读更多...
svg mask和stroke冲突问题

svg mask和stroke冲突问题

目录 先说结论各种样例首先是水平、垂直的线然后是斜线如果是图形加stroke呢用《g》标签包起来呢 总结 先说结论 实际上svg里&#xff0c;mask对svg内元素起作用的并非元素本身&#xff0c;而是元素几何形状的外包矩形&#xff0c;特别是和stroke有冲突&#xff0c;会产生奇怪…
阅读更多...
opencv 进阶16-基于FAST特征和BRIEF描述符的ORB（图像匹配)

opencv 进阶16-基于FAST特征和BRIEF描述符的ORB（图像匹配)

在计算机视觉领域&#xff0c;从图像中提取和匹配特征的能力对于对象识别、图像拼接和相机定位等任务至关重要。实现这一目标的一种流行方法是 ORB&#xff08;Oriented FAST and Rotated Brief&#xff09;特征检测器和描述符。ORB 由 Ethan Rublee 等人开发&#xff0c;结合了…
阅读更多...
工作7年的测试员，明白了如何正确的“卷“

工作7年的测试员，明白了如何正确的“卷“

背景 近两年&#xff0c;出台和落地的反垄断法&#xff0c;明确指出要防止资本无序扩张。 这也就导致现在的各大互联网公司&#xff0c;不能再去染指其他已有的传统行业&#xff0c;只能专注自己目前存量的这些业务。或者通过技术创新&#xff0c;开辟出新的行业。 但创新这种…
阅读更多...
vmware 虚拟机开机自启动脚本

vmware 虚拟机开机自启动脚本

1、建立一个txt文件 D:\VMware\VMware Workstation\vmrun.exe -T ws start "I:\Documents\Virtual Machines\centos\centos.vmx" nogui 注意&#xff1a;如果路径中有中文需要先转换txt文件编码格式ANSI 2、设置bat开机自启动 winr shell:startup 复制文本文件到…
阅读更多...
【uniapp】微信小程序 ， 海报轮播图弹窗，点击海报保存到本地，长按海报图片分享，收藏或保存

【uniapp】微信小程序 ， 海报轮播图弹窗，点击海报保存到本地，长按海报图片分享，收藏或保存

uivew 2.0 uniapp 海报画板 DCloud 插件市场 第一步&#xff0c;下载插件并导入HbuilderX 第二步&#xff0c;文件内 引入 海报组件 <template><painter ref"haibaorefs"></painter> <template> <script>import painter from /comp…
阅读更多...
Docker关于下载，镜像配置，容器启动，停止，查看等基础操作

Docker关于下载，镜像配置，容器启动，停止，查看等基础操作

系列文章目录 文章目录 系列文章目录前言一、安装Docker并配置镜像加速器二、下载系统镜像&#xff08;Ubuntu、 centos&#xff09;三、基于下载的镜像创建两个容器 &#xff08;容器名一个为自己名字全拼&#xff0c;一个为首名字字母&#xff09;四、容器的启动、 停止及重启…
阅读更多...
汽车检测报告小程序开发制作方案

汽车检测报告小程序开发制作方案

传统的车辆检测流程通常繁琐且耗时&#xff0c;用户对更快速、便捷的检测方式有了更高的期望。基于这一需求&#xff0c;开发一款汽车检测报告小程序将成为现实生活中的实用工具。 产品定位为一款提供汽车检测报告查询的小程序&#xff0c;主要服务于需要进行汽车检测的车主、…
阅读更多...
【Leetcode】移动零

【Leetcode】移动零

移动零 题目描述算法描述编程代码 链接: 移动零 题目描述 算法描述 编程代码 class Solution { public:void moveZeroes(vector<int>& nums) {//题目要求不可以复制数组&#xff0c;开辟额外空间int dest -1,curr 0;for(;curr < nums.size();curr){if(nums[cu…
阅读更多...
正中优配：股票增发对散户有补偿吗？

正中优配：股票增发对散户有补偿吗？

股票增发指的是公司发行新的股票&#xff0c;从而添加公司的股本。这通常是为了筹集资金&#xff0c;以用于公司的扩张或其他出资。可是&#xff0c;这种操刁难散户出资者的影响往往被疏忽或被低估。本文将从多个角度剖析股票增发对散户出资者的影响&#xff0c;包含股票价格、…
阅读更多...
荣耀重返印度市场，代工订单闻泰承接 | 百能云芯

荣耀重返印度市场，代工订单闻泰承接 | 百能云芯

荣耀宣布将重新进军印度市场&#xff0c;最新的消息显示&#xff0c;荣耀已与闻泰科技达成协议&#xff0c;委托其承接印度手机市场的制造订单。此举旨在通过在闻泰科技的印度工厂进行组装&#xff0c;降低关税&#xff0c;从而提升荣耀产品在印度市场的竞争力。 作为备受瞩目的…
阅读更多...
分库分表之拆分键设计 | 京东物流技术团队

分库分表之拆分键设计 | 京东物流技术团队

众所周知&#xff0c;在现实世界中&#xff0c;每一个资源都有其提供能力的最大上限&#xff0c;当单一资源达到最大上限后就得让多个资源同时提供其能力来满足使用方的需求。同理&#xff0c;在计算机世界中&#xff0c;单一数据库资源不能满足使用需求时&#xff0c;我们也会…
阅读更多...
Andorid广播

Andorid广播

以下内容摘自郭霖《第一行代码》第三版 文章目录 一、广播机制简介1.1 广播的类型1.1.1 标准广播1.1.2 有序广播 二、接收系统广播2.1 动态注册监听时间变化2.2 静态注册实现开机启动 三、发送自定义广播3.1 发送标准广播3.2 发送有序广播 一、广播机制简介 1.1 广播的类型 A…
阅读更多...
EPS倾斜摄影模型测图

EPS倾斜摄影模型测图

1、打开EPS软件&#xff0c;新建工程。 2、加载倾斜摄影模型。在三维测图--倾斜摄影--加载本地倾斜模型中&#xff0c;加载模型到工作空间。 3、加载后的结果如下&#xff1a; 4、开始绘制房屋。选择编码--进入加线模式--开始绘图。 开始绘图图形&#xff0c; 5、绘图按键使用 …
阅读更多...
面试题大揭秘！Java中== 与equals的区别？

面试题大揭秘！Java中== 与equals的区别？

大家好&#xff0c;我是你们的小米&#xff01;今天我们要来聊一个在Java面试中经常被问到的问题&#xff1a; 与 equals 的区别。这可是一个重要而且常常令人头疼的问题哦&#xff01;废话不多说&#xff0c;咱们马上开启今天的探索之旅吧&#xff01; 背景知识 在开始深入探…
阅读更多...
什么是雨量气象站？

什么是雨量气象站？

过多的强降水会造成重大自然灾害&#xff0c;给我们的生活带来很大影响&#xff0c;实时监测降雨信息&#xff0c;能够及时发布气象预警&#xff0c;防范可能因强降水引起的山洪、泥石流等自然灾害&#xff0c;保护人民群众生命财产安全&#xff0c;提高防灾减灾能力。 雨量气…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023