实现原理

通常来说，二分查找的使用范围是当数组有序的时候可以使用，可以进行对有序数列的搜索，但其实这样的说法不完全正确

严格来说，二分查找可以适用于有二段性的数组序列中，二段性就是可以把一个数组的区间划分为两个部分，然后通过一定的判断舍弃掉其中一部分，在另外一个区间内继续寻找，这样的数组序列就是有二段性的序列，因此，数组有序是具有二段性的一种情况，但是二段性并非要求一定是要有序的

查找区间左右端点

查找左端点

这个算法原理是朴素二分的一个延伸，它的使用范围通常作用于例如要寻找一段符合二段性序列的子区间的情况，例如现在有序列1，2，3，3，3，3，4，我们要寻找的是包含3的这段区间的下标情况，因此这里就需要进行这段区间左右端点的寻找

首先是进行左端点的寻找：

核心思维不变，依旧是找中间然后进行左右区间的简化，但是和朴素二分查找比起来却也有很多需要进行注意的地方

算法思路：

算法思路和前面相比有一些不同，以上面的例子为例，假设我们要寻找的是3，那么就将这个区间划分为两个部分，小于3的部分和大于等于3的部分

那么我们定义了left和right指针，当两个指针求出mid指针后，就可以进行分类讨论了：

mid对应的下标小于3：此时意味着mid对应的值一定不是我们需要的值，因此这里就可以放心的让left=mid+1
mid对应的下标大于等于3：此时意味着mid已经落到了我们要关注的区间内，那么此时right就不能再和朴素二分查找一样选择right=mid-1了，应该把他改为right=mid，才能符合要求，否则可能会遗漏掉右边区间的数据

细节处理：

循环条件的判断要采用left<right
left == right的情况下，就是最终结果，不需要进行判断了
如果进行判断，就会死循环
求中点的操作：

mid=left+(right-left)/2
mid=left+(right-left+1)/2

对于朴素二分来说，这两种都是可以的，究其本质这两个的区别是，当序列的数量是偶数的时候，查找到的中间元素其实是两个数，上面的式子对应的是这两个数中的左数，下面的式子对应的是这两个数中的右数

而在这里端点寻找的算法中，只能采用上面的式子，原因其实和算法原理中对右区间的处理有分不开的联系，如果这里采用的是下面的式子，那么mid的值更新和right的值更新是相同的，就会陷入死循环，程序跑不下去

查找右端点

和查找左端点的算法相同，查找右端点也是基于二段性，分为小于等于的区间和大于的区间，不同的点在于left和right的处理方式和选中点的形式和前面相反

left=mid
right=mid-1
mid=left+(right-left+1)/2

实现思路

和前面的算法不同，二分查找拥有一定的模板性，但模板并非硬套，需要在实际理解二分算法的本质的前提下，进而利用模板类的语句更方便的解决二分查找的问题

朴素二分查找模板

while (left <= right)
{
    int mid = left + (right - left) / 2;
    if (nums[mid] == target)
    {
        return mid;
    }
    else if (nums[mid] < target)
    {
        left = mid + 1;
    }
    else
    {
        right = mid - 1;
    }
}

查找区间左右端点模板

这个模板也是基于题目总结出的

while (left < right)
{
    int mid = left + (right - left) / 2;
    if (nums[mid] < target)
    {
        left = mid + 1;
    }
    else
    {
        right = mid;
    }
}

while (left < right)
{
    int mid = left + (right - left + 1) / 2;
    if (nums[mid] > target)
    {
        right = mid - 1;
    }
    else
    {
        left = mid;
    }
}

下面出现-1的时候上面就+1

典型例题

二分查找

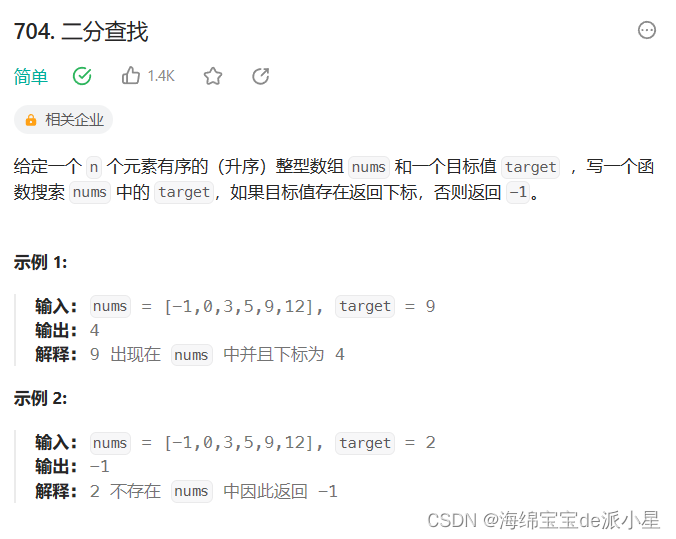
最入门的一道题，从中可以抽离出朴素二分查找模板

class Solution 
{
public:
    int search(vector<int>& nums, int target) 
    {
        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]==target)
            {
                return mid;
            }
            else if(nums[mid]<target)
            {
                left=mid+1;
            }
            else
            {
                right=mid-1;
            }
        }
        return -1;
    }
};

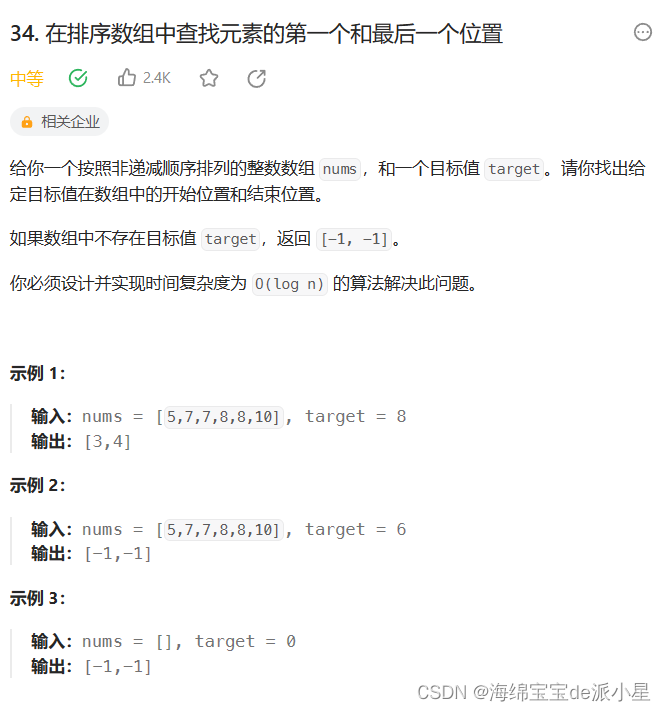
查找元素第一个和最后一个位置

class Solution 
{
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        vector<int> v;
        if(nums.size()==0)
        {
            return {-1,-1};
        }
        int left=0,right=nums.size()-1;
        while(left<right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]<target)
            {
                left=mid+1;
            }
            else
            {
                right=mid;
            }
        }
        nums[left]==target? v.push_back(left) : v.push_back(-1);

        left=0,right=nums.size()-1;
        while(left<right)
        {
            int mid=left+(right-left+1)/2;
            if(nums[mid]>target)
            {
                right=mid-1;
            }
            else
            {
                left=mid;
            }
        }
        nums[right]==target? v.push_back(right) : v.push_back(-1);
        return v;
    }
};

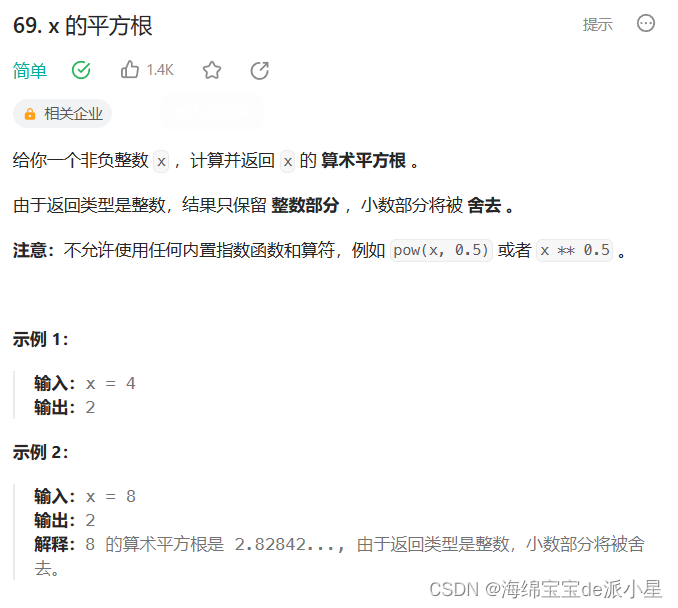
x的平方根

class Solution 
{
public:
    int mySqrt(int x) 
    {
        if(x==0 || x==1)
        {
            return x;
        }
        int left=1,right=x/2;
        while(left<right)
        {
            long long mid=left+(right-left+1)/2;
            if(mid*mid<=x)
            {
                left=mid;
            }
            else
            {
                right=mid-1;
            }
        }
        return left;
    }
};

对上面查找左右端点二分的另外一个应用，是上面的简化版，只需要查找一半，这里需要注意的是，在使用模板前要想清楚是如何进行分类讨论的，我们这里采用的分类讨论的思想是，如果平方的和小于等于x就保留，如果大于x就直接舍弃，这就是对这段区间的二段性进行的讨论，因此如果mid落入了大于x的区间内就直接被舍弃，right=mid-1，下面出现减号上面就加号，本质上是因为要考虑到中间两个数答案恰好落在左边的情况

山脉数组峰顶索引

class Solution 
{
public:
    int peakIndexInMountainArray(vector<int>& arr) 
    {
        int left=0,right=arr.size()-1;
        while(left<right)
        {
            int mid=left+(right-left+1)/2;
            if(arr[mid]>arr[mid-1])
            {
                left=mid;
            }
            else
            {
                right=mid-1;
            }
        }
        return left;
    }
};

本题就体现出，二分查找未必一定要求是有序，其实只要包含二段性就可以使用二分查找，在这个题的原理中，这个序列有天然的二段性，即左边满足严格大于，右边满足严格小于，由于题目保证长度大于等于3，因此这里采用的是让mid和mid-1对应的数据进行比较，因此我们就把二段性划分成两部分：左边严格递增一段，右边严格递减一段，如果mid落在了严格递减的这段区间内，表示mid一定不会是这段区间，因此就选择right=mid-1，而如果落在左边的区间内，就代表着mid不确认是不是最高的点，因此就选择让mid=left