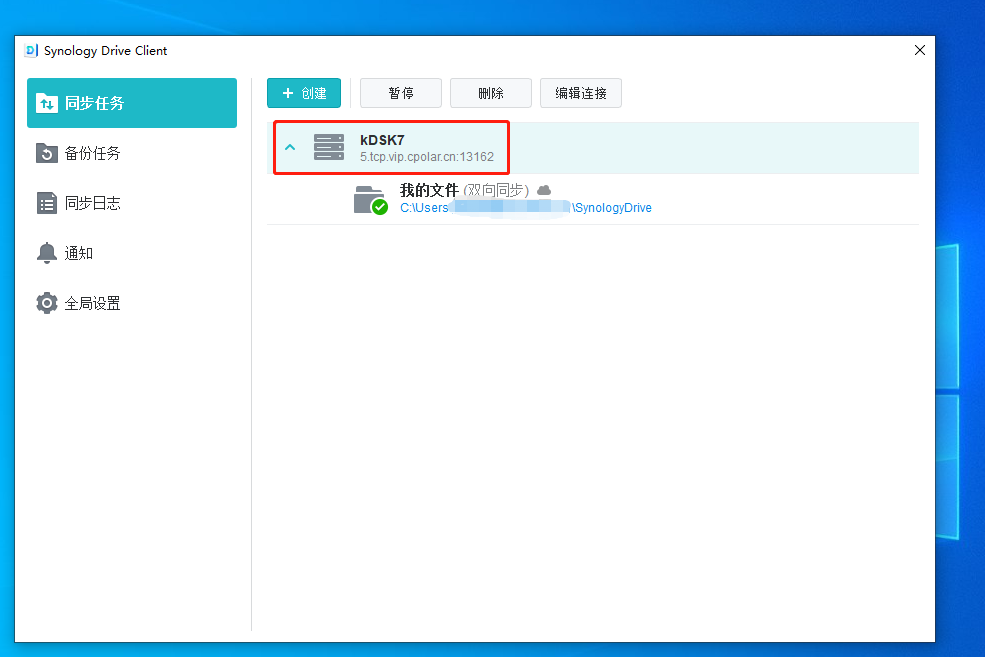
形如:
y
′
+
p
(
x
)
y
=
q
(
x
)
(1.first)
y' + p(x)y = q(x) \tag{1.first}
y′+p(x)y=q(x)(1.first)
的方程叫做一阶线性微分方程。
同济版教材的求解方法是常数变异法,初次接触感觉主编的脑回路异常清奇,自己怎么也get不到核心要义。一直到现在都感觉云里雾里,摸不到方向,不明白课本里的逻辑到底是要表达什么,如果谁能用简单易懂的方法证明一下,我是很乐意接受指教的。
下面说一下我在知乎上手的启发和我自己的感悟。
知乎上关于常数变异法的解释通俗易懂,大意是:
- 等式乘以u(x),左边凑分部积分。那么可以做出如下变换:
y ′ u ( x ) + y u ( x ) p ( x ) = q ( x ) u ( x ) (1.0) y' u(x)+ y u(x)p(x) = q(x)u(x) \tag{1.0} y′u(x)+yu(x)p(x)=q(x)u(x)(1.0)
等式的左边看作是 y u ( x ) y u(x) yu(x)两个函数的积求微分的形式,根据微分的乘法公式可得:
[ y u ( x ) ] ′ = q ( x ) u ( x ) (1.1) [y u(x)]' = q(x)u(x) \tag{1.1} [yu(x)]′=q(x)u(x)(1.1)
y = ∫ q ( x ) u ( x ) d x u ( x ) (1.2) y = \frac{ \int q(x)u(x)dx}{u(x)} \tag{1.2} y=u(x)∫q(x)u(x)dx(1.2)
上面的变换成立的基础条件是:
u
′
=
u
(
x
)
p
(
x
)
(1.3)
u' = u(x)p(x) \tag{1.3}
u′=u(x)p(x)(1.3)
此时的问题转化为,要找到一个函数u(x)满足(1.3)的条件。而根据微分方程的基础知识可知,这个函数可以分离微分变量,必定可以解出u(x):
d u u ( x ) = p ( x ) d x \frac{du}{u(x)} = p(x)dx u(x)du=p(x)dx
l
n
∣
u
(
x
)
∣
=
∫
p
(
x
)
d
x
+
C
ln |u(x)| =\int {p(x)dx} + C
ln∣u(x)∣=∫p(x)dx+C
u
(
x
)
=
C
e
∫
p
(
x
)
d
x
(1.4)
u(x) = Ce^{\int {p(x)dx} } \tag{1.4}
u(x)=Ce∫p(x)dx(1.4)
- 将(1.4)带入(1.2)可得方程 ( 1. f i r s t ) (1.first) (1.first)的一个特解为:
y = C ∫ q ( x ) e ∫ p ( x ) d x d x e ∫ p ( x ) d x y =C \frac{ \int q(x) e^{\int {p(x)dx} } dx}{e^{\int {p(x)dx} } } y=Ce∫p(x)dx∫q(x)e∫p(x)dxdx
课本中的描述能看懂,但是不明白,为什么要将常数代换为u(x),另外,对于接下来的描述,也无法从已有的知识中找到推理和
证明,证明逻辑上是完美自洽的。
望各位网友不吝赐教。
同济版课本中的描述如下: