1003 Many Topological Problems
每个节点序号和权值分开计算,两者的排列组合数相乘即为答案
对于序号的顺序,一共有n个位置,第一个位置可以放序号1,2,..n共n个点,第二个则可放置n-1个点,以此类推,排列组合数为n的阶乘
对于权值,从小到大放置,如果不考虑k的话,对于权值为x的数,可以接在权值为1,2...x-1的下面(x作为子节点),共x-1个数,然后再考虑k,对于权值为x的数,只能接在x-1,x-2,..x-k的下面,共k个数,所以权值为x的数的放置方式有min(x-1,k)种,由于权值是从2到n一个一个放置,分步计算,所以用乘法
数学知识,可以推公式
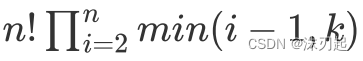
发现当n等于k时,答案为n!*(k-1)!
当n不等于k时,当i-1等于k时为分界点,答案为n!*k!(共k个数)*k^(n-1-k)(共n-1-k个数)
注意,快速幂,a^k中的k必须为正数
法一:
#include<iostream>
#include<algorithm>
#include<cstring>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e6+10,mod=1e9+7;
ll fac[N];
int n,k;
//快速幂
int qmi(int a,int k){
int res=1;
while(k){
if(k&1) res=(ll)res*a%mod;
a=(ll)a*a%mod;
k>>=1;
}
return res;
}
void solve() {
cin>>n>>k;
if(k==n) cout<<fac[n]%mod*fac[k-1]%mod<<endl;
else cout<<fac[n]%mod*fac[k]%mod*qmi(k,n-1-k)%mod<<endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
//预处理阶乘
fac[0]=1;
for(int i=1;i<=1e6;i++) fac[i]=fac[i-1]*i%mod;
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}法二:
#include<iostream>
#include<algorithm>
#include<cstring>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e6+10,mod=1e9+7;
int n,k;
void solve() {
cin>>n>>k;
ll ans=1;
for(int i=1;i<=n;i++) ans=ans*i%mod;
for(int i=1;i<=n;i++){
if(i>1) ans=ans*min(i-1,k)%mod;
}
cout<<ans<<endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}1004 Do You Like interactive Problems
算期望次数,就当作正常的次数,只不过分情况讨论,将不同概率和对应的次数相乘,然后全部相加(可以叠加,算出的低一层的期望次数仍可以和概率相乘并相加得到高一层的期望次数)
参考2023 hdu 第10场 1004 Do you Like Interactive Problem_TrRicky的博客-CSDN博客
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<ctime>
#include<set>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int mod=998244353;
int n;
int qmi(int a,int k){
int res=1;
while(k){
if(k&1) res=(ll)res*a%mod;
a=(ll)a*a%mod;
k>>=1;
}
return res;
}
int inv(int x){
return qmi(x,mod-2);
}
void solve(){
cin>>n;
if(n==1) cout<<0<<endl;//当n为0时,直接特判,期望询问次数为0,因为只有一个数,这个数一定是x,都不需要询问
else cout<<(ll)(2*n-1)*inv(3)%mod<<endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}1012 Equalize the Array
只要保证最小的那个数出现的次数是最大的就行,这样就可以一直累加变大
因为只有次数最大的那个数才可以被操作,而且只能是变大,所以必须从最小的数开始变大
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<set>
#include<map>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=5e5+10;
int a[N];
int n;
void solve() {
cin>>n;
set<int>s;
map<int,int>mp;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
s.insert(a[i]);
mp[a[i]]++;
}
int x=*s.begin();
for(auto v:s){
if(mp[x]<mp[v]){
cout<<"NO"<<endl;
return;
}
}
cout<<"YES"<<endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}