个人网站：https://tianfeng.space

psbeta下载安装

链接：https://pan.baidu.com/s/1XbxSAFoXh0HDz6YbkrAzDg
提取码：e8pn

1.注册

https://account.adobe.com

adobe官网注册账户，有谷歌邮箱直接注册就行，注册年龄得大于18岁

2.安装ps beta

来到页面点击安装包，一直点下一步就行

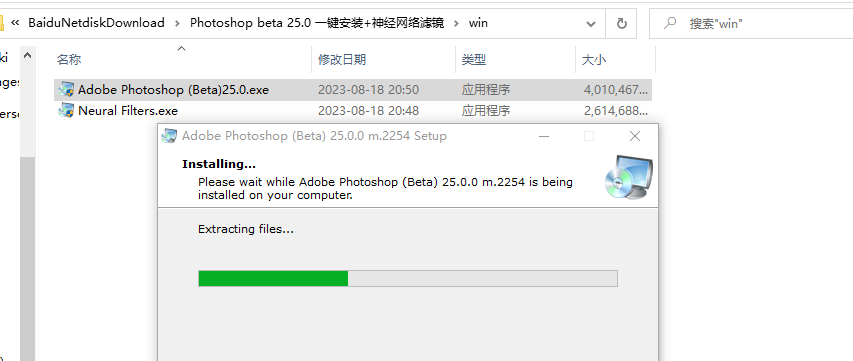
安装完毕，自动打开PS beta，再把中文包放到该目录下

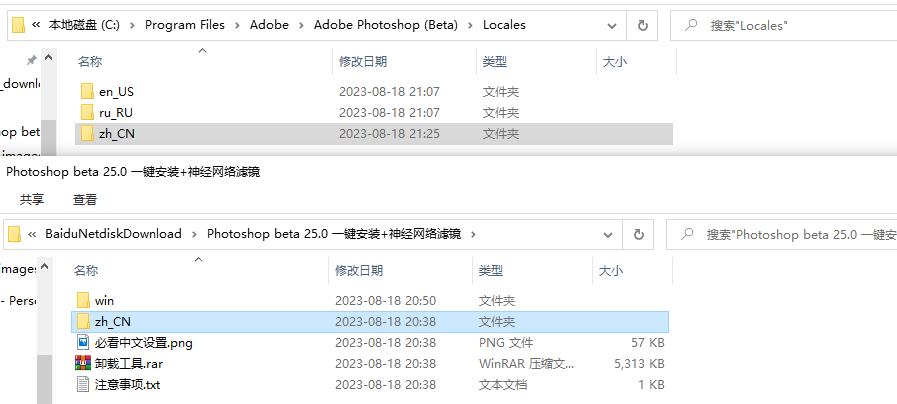
来到ps，依次选择如下

选择简体中文，ok

这个时候你可能还无法使用创建式填充功能，如果是第一次安装ps，这个时候需要登录账户，点击右上角帮助，有个登录选项，记得一定得是美国地区注册的大于18岁的账户，节点挂到美国注册，登录完后会提示可以使用了，神经网络滤镜在滤镜Neural Filters选项下

2.安装神经网络滤镜

点击第二个应用程序，一直下一步就行，很简单

3.使用

打开ps beta

简单演示下效果把，左键矩形框选中区域，输入文字，自动生成符合场景的物体，实在太方便了

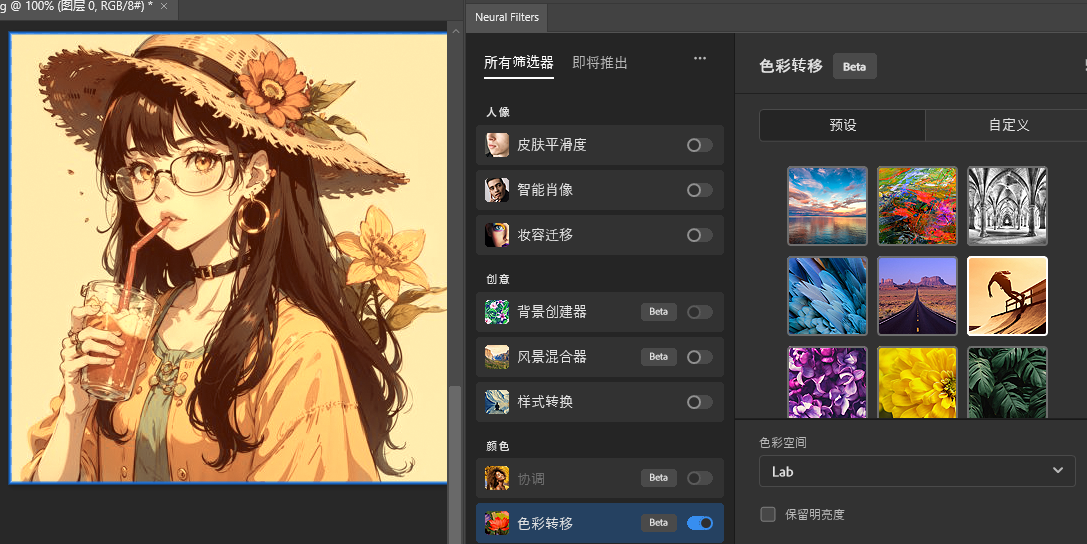
Draggan下载安装

链接：https://pan.quark.cn/s/84baac1b7afc
提取码：5AsQ

感谢万能君的软件库整合包

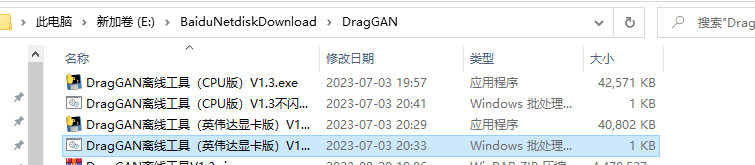
直接下载文件，在解压DragGAN离线工具V1.3，checkpoint放到改目录下，同时CPU点击第二个，gpu点击第四个启动

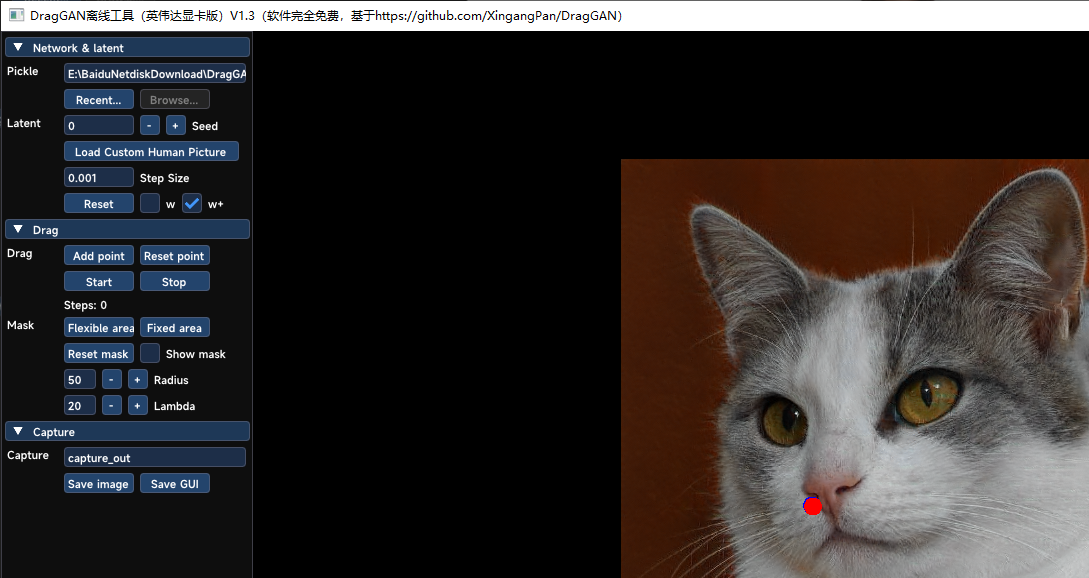
pickle是权重文件加载目录，recently是选择加载checkpoint目录下的文件，0是种子，点击add point第一个点为红点，第二个为蓝点，然后start，就开始移动了，点击最下面可以保存图片，

保存目录为，

现在只能基于训练的模型里的图片进行拖拽，像我们的图片想要修图，可能得把图片训练完保存权重然后加载才能使用，从结果来说，有点草单，就当科普一下吧！！！