现在我们续写上一章博客的内容（即99章博客的内容）

快速排序：

同冒泡排序一样，快速排序也属于交换排序，通过元素之间的比较和交换位置来达到排序的目的

不同的是，冒泡排序在每一轮中只把1个元素冒泡到数列的一端，而快速排序则在每一轮挑选一个基准元素

并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成两个部分，这种思路就叫作分治法

基准元素的选择（看如下例子）：

基准元素，英文是pivot，在分治过程中，以基准元素为中心，把其他元素移动到它的左右两边，当然，这是过程，后面会给出图解

我们可以随机选择一个元素作为基准元素（一般选择第一个），并且让基准元素和数列首元素交换位置

元素的交换：

选定了基准元素以后，我们要做的就是把其他元素中小于基准元素的都交换到基准元素一边，大于基准元素的都交换到基准元素另一边，也就是过程，后面有图解

双边循环法（看如下例子，不是上面的图片哦）：

首先，选定基准元素pivot（这里选择第一个位置，也就是4，或者你认为原来8的位置是4也行），交换后，然后与首位置元素交换，并且设置两个指针left和right，指向数列的最左和最右两个元素

接下来进行第1次循环：

从right指针开始（即right需要比left先移动，这是重合的前提），让指针所指向的元素和基准元素做比较，如果大于或等于pivot，则指针向左移动

如果小于pivot，则right指针停止移动，再切换到left指针

轮到left指针行动，让指针所指向的元素和基准元素做比较，如果小于或等于pivot，则指针向右移 动

如果大于pivot，则left指针停止移动，当他们都停止移动后，然后左右指针指向的元素交换位置

上面就是操作规则，后面都按照这样来操作

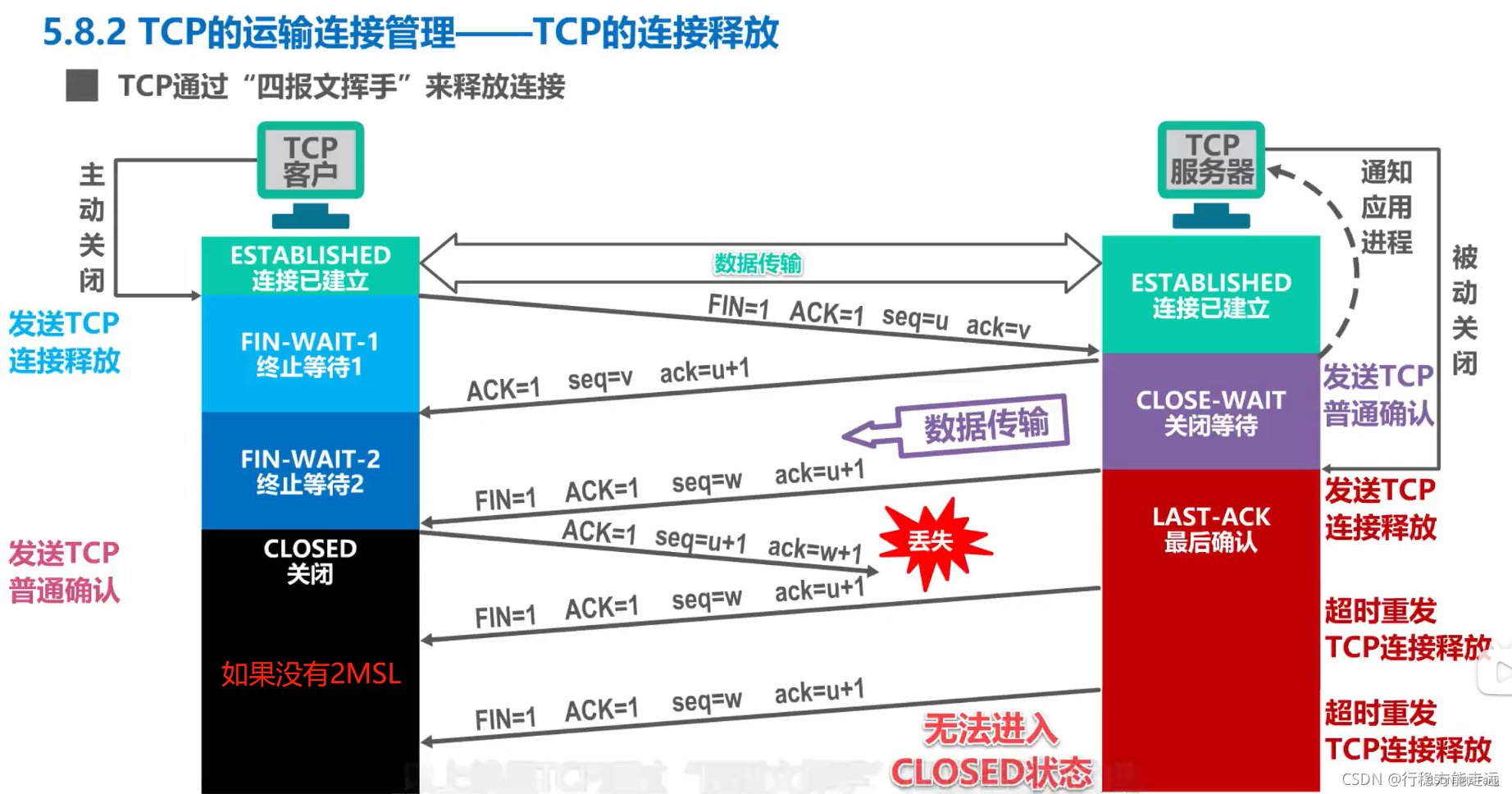
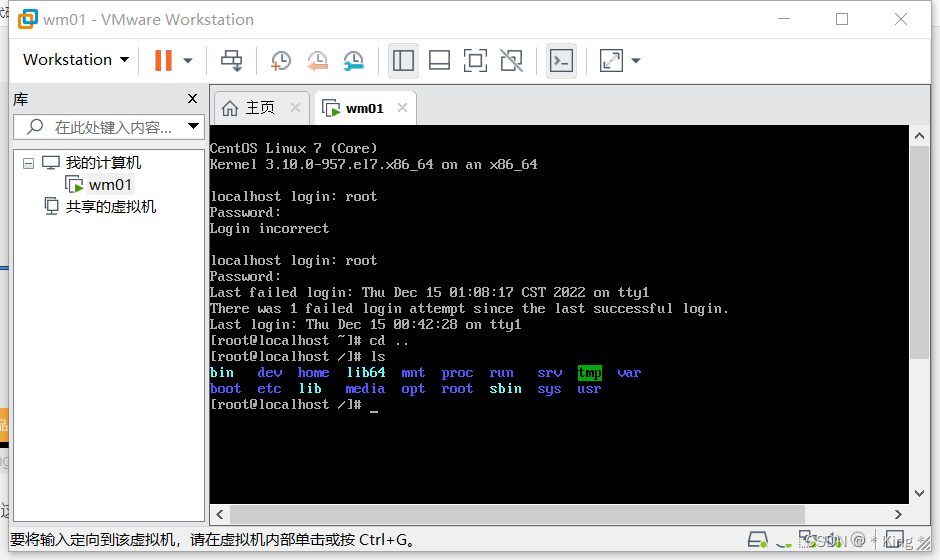
由于left开始指向的是基准元素，判断肯定相等，所以left右移1位，所以在程序里面，可以选择直接先向右移动（即通常是+1），但是需要特殊的处理，再程序里会说明，这里选择操作+1

由于7>4，left指针在元素7的位置停下，这时，让left和right指针所指向的元素进行交换

接下来，进入第2次循环，重新切换到right指针，向左移动，right指针先移动到8，8>4，继续左移，由于2<4，停止在2的位置

只要重合就操作与首位置交换，所以right一般后面需要进行判断操作

我们可以看到，最后的结果是3，1，2，4，5，6，8，7，所以可以看到原来基准4的左边的确比他小，右边也的确比他大，即前面我们说过的过程就是上面的图解

然后我们会进行再次的分治，当然，再这之前，我们需要以left以及right重合的部分，进行分开，即我们分开成3，1，2，4（包含重合部分）以及5，6，8，7，然后在他们两个之间都自己选择一个基准，再次的排序，如果3，1，2，4，选择了2，以及5，6，8，7，选择了6，过程如下：

/*
3 1 2 4
2 1 3 4
1 2 3 4，你选择随机或者第一个都行，因为由于right和left的操作，所以通常会打乱原来的顺序，因为需要得到比2小的和比2大的（之所以是通常，看后面给出的原因即可）
然后继续分开，那么就是1 2和3 4，直接判断即可

5 6 8 7
6 5 8 7
5 6 8 7，这里可以发现一个问题，我们选择了6，结果确相同，而我们选择5就是6 5 8 7（left加了1的情况），当然再次的选择6
又会变成5 6 8 7了（但再次的选择一般都会分开，只是随机可能导致不变，所以我们一般都取第一个），所以可以发现，即这个时候可以发现，随机的取或者取第一个，由于因为我们选择的地方，左右操作始终只是在第一个left，且后面的right必然到第一个left，所以基本循环了，当然，这是分治的一个隐藏的重合，但并没有什么问题，因为你可以通过判断，来使得如果第一个right直接到left，那么就直接的取基准而不用判断left了（当然，一般他后面有具体相同的操作，所以我们也不会进行判断，因为就算你判断了，不也是需要交换，那么总体还是不好，因为你的判断，其他情况都需要操作，即判断多了，因为总不能为了你一个小提升，而牺牲其他情况吧，一般来说，只有总体的提升，我们才会进行操作，比如后面的移动，就能节省两次判断，而我们只需要一个判断就可，且他是最后判断的，所以有显示的提高），当然就算重合了也没有关系，反正会操作继续分开，只是加上我们的判断，可以稍微提高那么一丢丢的性能，但不建议（上面括号里面已经说明了）
然后继续分开，因为操作一次就要分开，因为都是在第二个即5的为（取6）或者6的位置（取5）重合
所以我们分成5 6和8 7
现在，我们直接判断即可，不用取了，因为会导致交换或者不变（因为取第一个，那么直接交换，取第二个，那么操作了两次交换，一个首部交换，一个重合交换，那么不变）
那么判断之后，就是5 6和7 8了，在程序里有体现，当然，上面是因为先将left+1的，所以需要有判断（防止5 6交换），如果不操作加1，那么自然就会自动的排序好的，而不会进行与第二个交换，因为与自己交换了（即与第一个，对应与5 6中的5，所以使得自动排序，你可能不懂，看代码即可，后面会说明）

从上面看，我们可以知道，我们选择的基准，会持续的以我们选择的进行分开，所以可以发现，他的选择，好像与二叉树的节点一样，只是他没有操作自平衡，即他的这个操作我们可以大致的认为是O(logn)，范围是O(n)到O(logn)，即前面的[10~1]，没有0.99，如果刚好都是一半，那么可以认为是O(logn)，而如果取的是这样的，比如1 2 3 4 5 6 7 8，我取8，然后慢慢的减1，可以是如下：
1 2 3 4 5 6 7 8（因为我们不知道他是否排序好的）
8 2 3 4 5 6 7 1
1 2 3 4 5 6 7 8
分开变成1 2 3 4 5 6 7和8（单独的不用操作），那么以此类推
第二次：1 2 3 4 5 6 
第四次：1 2 3 4
第七次：1，即第七次得到，很明显，与之前的冒泡一样，也是8-1=7次，所以这种情况我们也会认为是O(n)（n代表拆分几次，一般时间复杂度的n代表执行次数，虽然前面说过代表总数，但是是对于他们那里表示的，实际上总数也可以是总次数，比如循环的次数，所以n的意思还是没有变的，即是总数）
但总体来说，他的交换（即分开，注意是分开），是O(logn)（因为需要极端情况下，才会是O(n)，类似于二叉树，其他情况下，由于省略的关系，基本都会是O(logn)），但是他也只是交换（分开）而已，他们本身需要进行对比，即right和left的判断大小移动，那么他是多少次呢，很明显，总体比较7次（因为基准占用一次，且结合分开的来说就是7次，只是只有分开的7次），那么我们可以认为他的比较是O(n)（操作了省略），虽然是n-1（这里的n代表总数值长度）
而正是因为是分开的7次，且分开可能只需要3次即可，即logn，所以总时间复杂度就是O(nlogn)

这里只是进行解释，具体还是看后面的代码来体会的
*/

单边循环法：

单边循环法只从数组的一边对元素进行遍历和交换

开始和双边循环法相似，首先选定基准元素pivot

同时，设置一个mark指针指向数列起始位置， 这个mark指针代表小于基准元素的区域边界

这里还是以第一个作为基准

接下来，从基准元素的下一个位置开始遍历数组

如果遍历到的元素大于基准元素，就继续往后遍历

如果遍历到的元素小于基准元素，则需要做两件事：

第一，把mark指针右移1位，因为小于pivot的区域边界增大了1

第二，让最新遍历到的元素和mark指针所在位置的元素交换位置，因为最新遍历的元素归属于小于pivot的区域

首先遍历到元素7，7>4，所以继续遍历

接下来遍历到的元素是3，3<4，所以mark指针右移1位

随后，让元素3和mark指针所在位置的元素交换，因为元素3归属于小于pivot的区域（很明显，这个区域就是mark之前的位置，包括自身，原来是0，即可以发现，mark相当于前面说的双边循环移动的left，只不过只将right的操作，直接操作遍历了，然后交换了）

即无论使用哪种方式都可以

按照这个思路，继续遍历，后续步骤如图所示

后面然后分开即可，与双边是一样的，他也是使得操作两边，且循环基本一致，所以也是O（nlogn）

我们可以发现，无论是单边循环还是双边循环，最后都要进行交换回来，因为我们需要操作两边的，否则就不符合两边了，你可能会有疑问，不交换好像也行，实际上是不行的，所以一般我们都会交换，在代码中可以体现（有解释）

现在我们来编写代码，你可以试着将代码看完后，再自行编写一下：

package com.lagou;

import java.util.Arrays;

/**
 *
 */
public class test4 {

    //由于双边循环和单边循环只是交换不同，所以可以使用他们的交换来操作

    //双边循环
    public static int two(int[] arr, int start, int end) {
        //我们得到了数值，以及他的起始操作和结尾操作的下标，我们只是给这个具体下标范围进行排序
        //首先，我们定义一个对应的支点pivot
        int pivot;
        //我们将第一个下标作为基准
        pivot = start; //实际上可以直接得到具体数值，来省略一些代码，你可以自己操作就行了，这里就不改变了

        //定义left，这是操作了+1，即前面说的，在程序里加1即可
        int left = start + 1;
        //定义right
        int right = end;


        while (true) {
            while (left < right && arr[right] > arr[pivot]) { //即，如果是相同的，也认为是小的，所以到最后，也可以操作排列，因为他对于我来说是相同，但对于其他来说可不是了
                right--;
            }


            while (left < right && arr[left] < arr[pivot]) { //即，如果是相同的，也认为是大的，所以到最后，也可以操作排列，因为他对于我来说是相同，但对于其他来说可不是了
                left++;
            }
            //上面都是操作while循环，所以只有对应的地方才会停止
//而操作left < right，是使得他们重合后，不进行移动，否则可能出现right已经重合了，但是left还移动了
            //这种情况也容易导致越界，因为left++，在最后时刻，可能超过了数组下标，比如，8 7，那么7后面还是会移动的，而操作了left<right就能避免上面说明的情况

            //如果还是left<right，即没有重合
            if (left < right) {
                int temp = arr[left];
                arr[left] = arr[right];
                arr[right] = temp;
                //操作了交换
                //交换后，我们可以发现，他实际上操作了一次必定的移动，实际上我们可以使得right和left进行移动
                right--;
                left++;
                //因为是right先操作，所以我们交换right即可，即需要后面的right--;使得去操作交换，这使得原来需要两个判断，只需要一个判断了，并且这个判断是最后才操作的，所以有显示的提高

            }

            //之所以加上大于是防止特殊情况，比如使得无限循环，因为上面基本不会操作下标了
            if (left >= right) {
                if (arr[right] > arr[pivot]) { //防止先移动后，出现了大的情况，因为我们需要交换使得左下右大
                    right--;
                    //除了防止上面的移动，也防止会与第二个进行交换（特别的是只剩下2个时，比如前面解释的5 6），因为我们手动操作int left = start + 1;，所以虽然程序里加了1，但是为了防止出现与第二个操作交换，这里也需要进行--
                    //你可能认为，我们不操作int left = start + 1;即可，但是确需要再次的判断，反正这里也操作了--，为什么不继续利用呢，所以要随机应变，当然，如果不操作上面的移动，那么你也可以不操作加1，即这里也可以不判断，你可以都进行删除，发现，结果也是一样的
                }
                //到这里代表重合
                //那么可以不交换吗，答：不能
                //如果不交换，那么对于分开来说，由于第一个必然会比之前的左边大，那么他会一直操作到最后一个，且由于不会交换，那么就会出现无限循环
                int temp = arr[right];
                arr[right] = arr[pivot];
                arr[pivot] = temp;
                //我们直接的退出
                break;


            }


        }

        return right; //这个位置代表重合的位置


    }

    //单边循环
    public static int one(int[] arr, int start, int end) {
        int pivot;
        //我们将第一个下标作为基准
        pivot = start;


        //定义mark，也是初始位置
        int mark = start;

        for (int i = start + 1; i <= end; i++) {
            if (arr[pivot] > arr[i]) {
                //如果i=mark，且是小的，那么直接make++即可，不用交换，因为自身交换自身，是没有必要的
                mark++;
                if (i != mark) {
                    int temp = arr[mark];
                    arr[mark] = arr[i];
                    arr[i] = temp;
                }


            }
        }
        //上面的循环完毕后，会自动的退出，那么得到的mark值就能直接的返回了
        //那么这里可以不交换吗，答：不能
        //因为单边的循环中，如果你没有操作交换，那么第一个必然是比其中一边都要大或者相同的，而由于必须小于第一个才会操作++，所以导致如果没有交换
        //那么对应的mark的值不变，所以如果不交换的话，那么必然导致无限循环，并且你可能会认为，操作减一不就行了，但是如果操作减1，你怎么保证被减去的值是排好的呢
        //所以在单边循环来说，必须操作交换
        int temp = arr[mark];
        arr[mark] = arr[pivot];
        arr[pivot] = temp;

        return mark;
    }

    //他们都返回一个对应的下标，实际上该下标就是操作分开的
    //这里给出为什么交换的主要原因，以及他是如何分开的
    //实际上根据上面的参数就可以知道，他的分开只是将对应的起始下标和结尾下标改变而已，导致可以分开
    //操作排序，即多次的操作排序
    public static void quickSort(int[] arr, int start, int end) {
        //我们可以发现，他的一个操作包含了两个操作，像这种操作中，包含了自身的操作，一般都会使用递归，因为递归就是自身操作自身，在前面我们也通过循环来分解递归，比如使用对应的栈等等，前面的二叉树的遍历就是，但已经说过了，我只使用简单（方便）的操作，所以这里就使用递归了，因为代码量少，如果你需要循环的，自己去百度吧（虽然说百度，实际上只要是浏览器即可，只是我以前在电脑上使用百度比较多，所以习惯了，虽然我现在是使用谷歌浏览器的url地址来访问了，虽然一般默认会是百度访问）
        //定义结束条件
        if (start >= end||arr==null) {
            return;
            //因为如果起始位置等于结尾位置，说明只有一个了，就不用操作了
        }

        //这里以单边循环为例子，得到对应的重合下标
        int mark = one(arr, start, end);
        //调用自身，即操作具体分开的数据，即如果没有操作交换，那么就是如下
        quickSort(arr, start, mark - 1); //在单边循环中，这个减1可以不加（加上是为了减少判断），因为单边循环的操作，由于小的会在前面，大的会在后，所以就算操作自身也没有问题，且无论怎么分，都会导致局部的判断是小在前，大在后（因为反正分的时候，由于取已经分好的地方，再次的分，所以通常会导致只剩下3个或者2个时，必然可以会使得排序完毕，有些3个需要变成2个，比如3 1 2，即2个实际上才是必然排序完毕的）
        //所以我们可以感受到，就算不考虑数学的计算时间复杂度，那么由于他操作了分开的，就不用再次的判断左右两边的大小，所以很明显，就不用操作他们之间的联系了，而不是只会给出一个，所以比单纯的循环要好，因为单纯的循环，就算你已经分好了，也只能确定一个，而这里直接整体确定，且外加了基准这一个
        //所以他的最差也是与循环一样，都是必须确定一个，但是他这里还有整体的确定，所以的确比循环要好
        quickSort(arr, mark + 1, end);
        //因为是自身调用自身，所以对于其自身来说，给出的范围就相当于他们的start和end

    }

    //操作双边循环
    public static void quickSort1(int[] arr, int start, int end) {
        //定义结束条件
        if (start >= end||arr==null) {
            return;
            //因为如果起始位置等于结尾位置，说明只有一个了，就不用操作了
        }

        //这里以单边循环为例子，得到对应的重合下标
        int pivot = two(arr, start, end);
        //调用自身，如果没有操作交换，那么就是如下
        quickSort1(arr, start, pivot - 1); //双边循环也可以不减去1，因为与单边一样，看单边的解释即可（因为交换的本质是一样的）
        quickSort1(arr, pivot + 1, end);


    }

    public static void main(String[] args) {
        int[] arr = new int[]{4, 7, 3, 5, 6, 2, 8, 1};
        quickSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
        arr = new int[]{4, 2, 3, 5, 6, 7, 8, 1};
        quickSort1(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));

        //当然，相同怎么办，实际上并不需要理会，根据代码来说，相同的如果没有满足小于或者大于，那么一般都是认为是大的或者小的
        //实际上他必然也是排序好的，因为对于自己来说，是相同，但是对于其他人来说就不是了
        
        //当然，这里的数组不要是空的，否则arr.length - 1这里就会报空指针异常
    }
}

至此，单边和双边都操作完毕，他们实际上都是局部的进行操作，先进行分开，然后局部分开，所以使得除了他们自身的移动次数n外（整体来看就是n，因为无论你是否分开，判断的次数，只是从8到4+4而已），只需要操作logn次数即可，因为是分开的吗（前面已经说明过了）

即：快速排序的时间复杂度是：O（nlogn）

堆排序：

堆排序：堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法

堆是具有以下性质的完全二叉树

大顶堆：每个结点的值都大于或等于其左右孩子结点的值

小顶堆：每个结点的值都小于或等于其左右孩子结点的值

我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中：

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]，2i+2写成2*（i+1）也可

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点

将其与末尾元素进行交换，此时末尾就为最大值，然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值

如此反复执行，便能得到一个有序序列了

构造初始堆：

将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，因为他找最大，降序采用小顶堆，因为他找最小）

由于是完全二叉树，所以完全可以一路的定义过去，当我们通过数组创建了一个完全二叉树后，就可以继续下面的步骤了（你都可以解决红黑树，那么这个条件不难吧，具体思路：我们主要的难点就是如何进行连接节点，由于数组的存放，对应公式，即对应节点，我们可以利用这种，来保存一个list集合，然后让list集合也这样的根据公式进行连接，然后再根据公式进行赋值，那么一个数组就变成了二叉树了，后面会给出具体操作的），或者就是一个数组，而不操作二叉树也行，那么就只需要定义数组了，在后面的代码中就以数组为例子

此时我们从最后一个非叶子结点开始（叶结点自然不用调整，这里的第一个非叶子结点 arr.length/2- 1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整，为什么是这样的公式，我们看图，假设总节点为n，我们有四种情况，即叶子节点只有1个，2个，3个，4个，以下标为例子：

如果叶子节点是1个：那么n/2-1，就是第一个非叶子结点，比如4/2-1=1，举例：如果上面就到5，那么4/2-1=1，刚好就是6，即正确

如果叶子节点是2个：那么也是n/2-1，举例：如果上面到9，那么5/2-1，也是6，即正确

如果叶子节点是3个：那么如果是n/2-1，举例：如果上面8后面加上了左节点7，那么6/2-1=2，到8了，即也是第一个（8变成了非叶子节点了）

如果叶子节点是4个，那么如果是n/2-1，举例：如果上面8后面加上了右节点10，那么7/2-1=2，还是8，即也是第一个

实际上我们可以看到，他就是来算出最后一个非叶子节点的，实际上我们也可以通过公式来说明，我们知道，在下标为0来算时，一个非叶子节点的左右节点是2i+1和2i+2，那么如果这两个是最后两个，就说明他们的父节点，就是第一个非叶子节点，所以我们需要得出i的值，很明显，2i+2只需要除以2减1即可，但是前面的却不能，因为其中的1在过来时，是没有操作的，所以这个时候，他需要加上1，或者不除以2减1，那么只需要将2i+2减1即可，那么由于结果相同，且我们又可以发现，使用数组的长度，刚好就是arr.length/2- 1了

我们可以发现，为什么从0开始后，就要使用从1开始的计算方式（也就是个数），因为除法一般对于0开始有缺陷的（因为其他的数，在除2取整时，基本都有两个数的除以对应，而o只有1），否则一般需要加1来保证从1开始的计算方式（后续减1就行），或者通过减1，来满足缺陷，也就是使用下标，而不是个数，所以在前面的计算父节点的以及这里的除法都需要从1开始，否则前者偶数减1（因为3，4只要1），后者奇数加1（因为3，4，之后有减1，需要抵消），这是不同的解决方式，当然，这里是从0开始的，所以这里是后者，而之前的是前者，但无论怎么说本质上是起始数字的不同导致的，前面说明过了，而后者奇数加1的同时，偶数加1也没有问题，所以导致使用数组长度也没有问题，所以就是arr.length/2- 1了

我们可以发现，如果探索本质，需要很多功夫，但是，如果你认为逻辑上是这样，那么只需要知道他们的规律即可，而不需要知道为什么是这样的规律，所以上面的解释可以选择忽略，只需要知道arr.length/2- 1就能求出最后一个非叶子节点即可

上面我们找到了最后一个非叶子节点，所以我们能够得出他的值，并且也能得出他们三个的大小，我们将非叶子节点于他左右节点中最大的进行交换，如果他就是最大的，那么就操作后面的

找到第二个非叶节点4，由于[4，9，8]中9元素最大，4和9交换，那么第二个非叶子节点怎么找呢，很简单，数组长度，减去1即可，使得可以找到第二个非叶子节点，然后重新前面的步骤即可，因为堆是完全二叉树，那么他的前一个节点，必然是有左右节点的，否则他是不会出现的

这时，交换导致了子根[4，5，6]结构混乱，继续调整，[4，5，6]中6最大，交换4和6

此时，我们就将一个无序序列构造成了一个大顶堆，我们发现，前面的操作都是为了将大的往上面走，并且是所以的非叶子节点，那么执行多少循环呢，一般需要二叉树的高度，你可以发现，将子树的数目认为是n，高度认为是x（从1开始，这里就不从0开始了），那么对应的循环次数就是n+x-1（只会操作被交换的往后面走，所以是x-1，在程序里面会有体现，而-1，代表根节点不用考虑了，因为已经是最大的，只需要考虑其他的高度的地方），一般来说，n个子树，对应的节点数是2n到2n+1，而高度x对应的节点数是x到x^2-1

相反，如果节点数是n，那么就有n/2个子树，和n的平方根个高度（这里取平均），所以总循环次数对于总结点来说就是"n/2+（n的平方根）-1"

那么总体来说，可以认为时间复杂度是O（n），因为n是最大的一个，对于n的平方根来说，在一开始虽然他是比logn要多的，中间少，然后又变多，即后面要多了，并且他们基本都比n/2也要少，长远来看（看图像就知道了），所以对于时间复杂度来说，n的平方根的时间复杂度是他们中是中等的（比logn多，那么时间复杂度就比他差，因为次数多，同理那么时间复杂度就比n/2好，即时间复杂度比n/2低，即比n/2好，因为时间复杂度越低越好），由于没有说明其时间复杂度，所以可以省略，即可以将"n/2+（n的平方根）-1"看成是n

将堆顶元素与末尾元素进行交换，使末尾元素最大，然后继续调整堆（除了交换后的那个元素），再将堆顶元素与末尾元素交换，得到第二大元素，如此反复进行交换、重建、交换即可

将堆顶元素9和末尾元素4进行交换

重新调整结构，使其继续满足堆定义

再将堆顶元素8与末尾元素5进行交换，得到第二大元素8

后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序，所以我们可以看到，他需要执行数组的次数，但是他的交换是变化的，可以发现，每操作一半数组的长度（跟着的），那么次数大概就会少一个平方根，所以平均看起来，可以发现，就是logn的次数，所以总时间复杂度是O（nlogn）（平均的认为，虽然实际上也是），n代表节点数

具体代码如下（你可以选择看完后，自己编写，因为有很多细节，所以建议先看，当然，若可以的话，也能先写好再看）：

package com.lagou;

import java.util.*;

/**
 *
 */
public class test5 {


    //首先我们需要定义一个操作最大堆的方法，问题是，这个方法的作用是什么，看如下解释：
    //参数的意思是：
    //array：需要操作的数组
    //start：要操作的起始下标（通常要是父节点）
    //last：要操作的结尾下标（对应父节点的后面的最终下标）
    //很明显，他是给数组进行操作范围来排序的，也就是说，给你这个子树来确定最大的值，即该子树变成最大堆
    public static void max(int[] array, int start, int last) {

        //首先需要得到他的左右节点，先得到左节点
        int chi = 2 * start + 1; //这里我们就定义一个数组来表示二叉树了，就不创建二叉树了
        while (chi <= last) {
            //如果他在数组里面，那么说明，有这个节点存在
            if (chi + 1 <= last && array[chi] < array[chi + 1]) {
                //到这里，说明左节点比，右节点小，那么就以右节点为主
                chi++;

            }
            if (array[start] > array[chi]) {
                //如果父节点最大，那么直接的退出即可
                break;

                //那么有个问题，前面的以右节点为主，以及这个的退出，难道不看没有操作的子节点的子节点是否有大于父节点的吗
                //答：有这个问题是正确的，实际上，我们在操作时，是认为他是最大堆的
                //也就是说，如果比他的左右节点大，那么必然比他的左右节点的子节点要大，在后面会给出具体的说明的


            }

            //然后操作交换
            int temp = array[start];
            array[start] = array[chi];
            array[chi] = temp;
            start = chi; //改变父节点
            //实际上我们可以发现，他移动的值是贯彻所有的，所以，最终都会赋值该原来的父节点，所以上面可以先不进行交换，我们可以先保存原来的父节点即可
            //当最后退出时，就进行赋值，当然，这样也能节省代码，所以这里可以进行改变


            //然后继续以对应交换的地方进行操作，因为交换的地方，会改变堆的
            chi = 2 * chi + 1;
            
            
            //很明显，上面他只会操作对应操作交换的节点，所以前面我会说成x-1

        }


    }

    //我们以及定义好的堆的操作，现在，我们来操作排序，在排序中，来解决得到最大堆的操作
    public static void sort(int[] array) {
        //将该数组变成最大堆
        //我们首先先传递对应的最后一个非叶子节点，那么必然他会操作交换然后退出，然后我们持续的将他减减即可，因为如果没有对应的子节点，那么必然，会超过数组长度，所以会退出
        //但由于他是完全二叉树，所以该退出的次数是基本没有的，否则，他又怎么出来呢，你说是吧（具体看完全二叉树的定义）
        for (int i = array.length / 2 - 1; i >= 0; i--) {
            max(array, i, array.length - 1);
        }
        //这样，就能每一个子树都操作了最大值，所以最终得到了最大堆，所以这就是前面的那个说明，因为我们是从左到右，从下到上的操作的
        //所以保证了后面都是最大堆，所以方法里，只需要交换即可，而不用考虑


        //接下来我们来操作最大的数，进行排序
        for (int i = 0; i < array.length - 1; i++) {

            //得到原来数组最后一个数
            int temp = array[array.length - 1 - i];
            array[array.length - 1 - i] = array[0];
            array[0] = temp;

            //然后再次的操作堆
            max(array, 0, array.length - 1 - 1 - i);
            //由于后面都是最大堆，所以方法里面只需要交换即可
        }


    }


    //上面我说过，可以不操作交换，具体代码如下：
    public static void max1(int[] array, int start, int last) {

        //先保存好原来的值，会贯彻所有的
        int temp = array[start];
        int chi = 2 * start + 1;
        while (chi <= last) {
            //如果他在数组里面，那么说明，有这个节点存在
            if (chi + 1 <= last && array[chi] < array[chi + 1]) {

                chi++;

            }
            //始终以原来的数据进行比对，因为交换也是如此
            if (temp > array[chi]) {

                break;


            }

            //然后操作交换
            array[start] = array[chi]; //直接赋值即可
            start = chi; //保存下一个父节点下标，因为以后赋值都是给他的


            chi = 2 * chi + 1;

        }
        //如果退出了，说明要么原来的节点最大，要么没有子节点了，那么将到达的那个下标赋值
        array[start] = temp;


    }


    public static void sort2(int[] array) {
        for (int i = array.length / 2 - 1; i >= 0; i--) {
            max(array, i, array.length - 1);
        }

        //这个for循环也进行改变
        for (int i = array.length - 1; i > 0; i--) {

            int temp = array[i];
            array[i] = array[0];
            array[0] = temp;

            max(array, 0, i - 1);
        }


    }

    //这里为了解决之前说过的量数组变成二叉树，所以这里定义一个节点类
    public class Node {
        int key;
        Node left;
        Node right;

        public Node(int key) {
            this.key = key;
        }
    }

    //保存头节点
    Node root;

    //将数组变成二叉树
    public void head(int[] array) {
        if (array != null) {
            List<Node> list = new ArrayList<>();
            //创建相同数目的节点
            for (int i = 0; i < array.length; i++) {
                list.add(new Node(0)); //先默认为0
            }
            //进行连接
            //首先赋值首节点
            list.get(0).key = array[0];
            root = list.get(0);
            for (int i = 0; i < list.size(); i++) {
                int left = 2 * i + 1;
                int right = 2 * i + 2;
                if (left < list.size()) {
                    list.get(i).left = list.get(left); //当没有对应的下标时，就不会进行赋值，那么自然就是null了
                    list.get(left).key = array[left];
                }
                if (right < list.size()) {
                    list.get(i).right = list.get(right);
                    list.get(right).key = array[right];
                }
            }
            //操作打印：
            //使用广度优先遍历，这样，可以很明显的看出是否与数组保持一致，广度优先遍历前面已经说明过了
            int[] result = new int[list.size()];
            int i = 0;
            Queue<Node> queue = new LinkedList();
            queue.offer(root);
            while (!queue.isEmpty()) {

                Node poll = queue.poll();
                result[i] = poll.key;
                i++;
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
            }
            String b = "";
            System.out.print("[");
            for (int ii = 0; ii < result.length; ii++) {
                if (ii == result.length - 1) {
                    b = b + result[ii] + "]";

                } else {
                    b = b + result[ii] + ",";
                }
            }
            System.out.println(b);
        } else {
            System.out.println("没有数组信息");
        }
    }

    //上面具体操作已经编写完成，现在我们来进行测试
    public static void main(String[] args) {
        int[] arr = {7, 6, 4, 3, 5, 2, 10, 9, 8};
        System.out.println("排序前：" + Arrays.toString(arr));
        sort(arr);
        System.out.println("排序后：" + Arrays.toString(arr));
        arr = new int[]{7, 6, 4, 3, 5, 2, 10, 9, 8};
        System.out.println("排序前：" + Arrays.toString(arr));
        sort2(arr);
        System.out.println("排序后：" + Arrays.toString(arr));
        test5 t = new test5();
        //打印对应的节点，如果他的值与数组基本对应（一样），说明节点连接成功
        //当然，里面也使用了二叉树变成数组的形式，所以实际上数组和二叉树之间，已经都完成了，所以广度优先遍历本质上就是二叉树变成数组的形式
        t.head(arr);
        //输出节点
        System.out.println(t.root);
    }
}

堆排序的时间复杂度是： O（nlogn），前面已经说明过了

计数排序 ：

计数排序，这种排序算法是利用数组下标来确定元素的正确位置的

假设数组中有10个整数，取值范围为0～10，要求用最快的速度把这10个整数从小到大进行排序

可以根据这有限的范围，建立一个长度为11的数组，数组下标从0到10，元素初始值全为0

假设数组数据为：9，1，2，7，8，1，3，6，5，3

下面就开始遍历这个无序的随机数列，每一个整数按照其值对号入座，同时，对应数组下标的元素进行加1操作

例如第1个整数是9，那么数组下标为9的元素加1

最终，当数列遍历完毕时，数组的状态如下：

该数组中每一个下标位置的值代表数列中对应整数出现的次数

直接遍历数组，输出数组元素的下标值，元素的值是几，就输出几次，0不输出

则顺序输出是：1、1、2、3、3、5、6、7、8、9

计数排序：适合于连续的取值范围不大的数组，可以为0（因为有0这个下标），不连续和取值范围过大会造成数组过大

如果起始数不是从0开始，比如分数排序：

95，94，91，98，99，90，99，93，91，92

数组起始数为90，这样数组前面的位置就浪费了

可以采用偏移量的方式：

比如，起始值为90，那么他们依次的减去90即可，使得可以不用创建很多个数组，当然，如果是无序的，或者说，不知道起始值，那么需要求出最小，在后面会说明

具体代码如下，可以先自己编写一遍：

package com.lagou;

/**
 *
 */
public class test6 {

    //计数排序的算法比较简单，有点类似于记录，在前面操作二分查找中，记录出现1次的那个使用hash的解释，就是记录的，与这个计数排序类似，只是他是哈希值来确定下标，而这里是值来确定下标（在那里也说明了这个）

    public static void Sort(int[] array, int offset) {
        //在前面的解释中，我们说明了偏移量，现在开始使用
        int[] a = new int[array.length];
        for (int i = 0; i < array.length; i++) {
            a[array[i] - offset]++;
        }
        //进行打印
        System.out.print("[");
        int ii = 0;
        for (int i = 0; i < a.length; i++) {

            while (a[i] != 0) {
                if (ii == 0) {
                    System.out.print(i + offset);
                    ii++;
                    a[i]--;
                } else {
                    System.out.print("," + (i + offset));
                    a[i]--;
                }
            }
        }
        System.out.println("]");


    }

    public static void main(String[] args) {
        int[] scores = {95, 94, 91, 98, 99, 90, 99, 93, 91, 92};

        Sort(scores, 90);
    }
}

计数排序的时间复杂度是O（n+m），当然，上面的先给出最小的，如果需要求出最小，那么基本只能将他们放入堆（最小堆）中来进行求出，只是可能需要nlogn时间复杂度了，当然这是不知道最小的情况，实际上就算我们不知道最小是多少，我们也可以使用空间换取时间，来变成O（n+m），只是不划算而已，特别是数很大时，即数越大越不划算，如果是10000，那么还是基本只能操作nlogn了（如果有其他好的方法，也可以使用），当然nlogn只是操作整体排序而已（因为包含数组），实际上如果只需要求出一个最大，那么也只需要O（n）（就一个，没有数组），在前面的堆的解释中可以知道的，所以计数排序的时间复杂度还是O（n+m），只是在不知道最小的情况下，可能是n+m+k，k是堆第一次排序的次数（前面堆中说明的n）

n：原数据个数（也就是数组的个数）

m：数据操作个数（第二个循环，也就是要操作的数据）

注意：第二个循环，因为0的存在，使得，需要多几次，所以这个m通常大于n，实际上这样也导致，没有必要的空间出现，所以为了解决这样的情况，我们一个会使用范围来操作，使得减少这样的情况，也就是使用后面的桶排序了

桶排序 ：

桶排序同样是一种线性时间的排序算法

桶排序需要创建若干个桶来协助排序

每一个桶（bucket）代表一个区间范围，里面可以承载一个或多个元素

桶排序的开始，就是创建这些桶，并确定每一个桶的区间范围具体需要建立多少个桶，如何确定桶的区间范围，有很多种不同的方式，我们这里创建的桶数量等于原始数列的元素数量，除最后一个桶只包含数列最大值外， 前面各个桶的区间按照比例来确定

区间跨度 = （最大值-最小值）/ （桶的数量 - 1）

为什么要创建的桶数量等于原始数列的元素数量，是因为最后一个桶可以更方便的操作最大值，在程序里会说明该问题

程序里也说明了可以不操作最后一个桶，当然，在时间复杂度上，也有原因，后面会说明

那么还有个问题：桶可以很少吗，或者很多吗，实际上都可以，只是由于若桶很少，那么对应的排序就需要更多，因为每多一个元素，就可能需要多排序对应长度的次数（具体参考冒泡排序，也可能增加一些次数，具体参考快速排序），而如果过少，那么占用的空间也非常大，所以我们操作平均，也就是桶数量等于原始数列的元素数量，一般都是这样来操作

那么在程序里面如果操作呢，答：使用公式：（当前值-最小值）*操作的桶数（这里是4，不考虑最后一个）/（最大值-最小值），这是为了确定当前值在桶里面的比例，因为他"操作的桶数/（最大值-最小值）“代表每"桶/值”，即可以认为是每多少桶代表1值（操作除法，一般要使得分母要为1），或者每1值，代表多少桶（也可以反过来说明的，只不过他是1而已，因为通常因为除法），因为他们是对应的关系，就如"位移/时间"，一样，每多少位移代表多少时间，或者每多少时间代表多少位移，只是计算具体的方式是位移在上的，从而得出速度，那么这里就代表下标，实际上很明显，因为最后一个数（最大的数）是独有的下标，所以对应的桶的数量一般都有减1来满足下标的情况，所以该公式的桶数量在这里也必然是4，这也是需要最后一个桶的原因，因为区间对比数量来说是少1的，所以在程序中，对应的桶数量要记得减1，否则下标会越界的，在代码中会详细的说明，这里可以先进行了解，实际上是因为区间的问题，所以无论是上面的区间跨度的桶数量，还是公式里面的下标的桶数量，都需要减1，程序里会说明的

假设有一个非整数数列如下：

4.5，0.84，3.25，2.18，0.5

以0.84为例，使用下标来表示就是0.84-0.5=0.34，0.34*4/4=0.34，代表0.34桶（值单位与值单位抵消），由于他先是减去0.5，所以将原来的值认为从0开始，那么0.34是小于1的，那么就是下标0，因为取整，正好也对应于下标，所以程序里就使用该公式来操作具体是那个桶了，而不是区间跨度（代表不是程序的公式）

遍历原始数列，把元素对号入座放入各个桶中

对每个桶内部的元素分别进行排序（显然，只有第1个桶需要排序）

遍历所有的桶，输出所有元素

0.5，0.84，2.18，3.25，4.5

具体的代码可以先看完下面代码后，自己编写：

package com.lagou;

import java.util.*;

/**
 *
 */
public class test7 {
    //定义方法来完成桶
    public static void Sort(double[] array) {
        //先得到最大值和最小值，来确定桶的范围和数量
        double max = array[0];
        double min = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
            if (array[i] < min) {
                min = array[i];
            }
            //这里有个问题，我们可以发现，如果对应的值等于max以及min，那么是怎样的呢，实际上既然等于，那么无论是max还是min，他的意思还是一样的，没有变，即max和min，即不用管

        }

        //得到他们之间的差
        double d = max - min;
        //因为桶里面包含多个数据，我们可以将这些数据用链表保存，那么保存链表，使用集合
        //为什么不使用数组呢，也可以，只是非常的麻烦，特别是下标（放入元素时，需要判断是否是同一个下标，并放入对应下标，那么需要将变量放在外面了，这样还是不够的，还需要为每个桶定义下标位置，实在麻烦，这里就不做说明了），且使用链表不需要考虑扩，所以使用链表容
        List<LinkedList<Double>> l = new ArrayList<>(array.length); //使用构造方法，固定list集合的大小，使得不会从10开始扩容
        //而是该大小开始进行扩容（一般是1.5倍，这是list集合的底层原理，假设是15，那么就是增加7，因为15操作>>1就是7，或者说，是一半，只是7.5是没有的，偏向于下方，因为不满1是不会进1的，所以0.5就是0）

        //创建桶
        for (int i = 0; i < array.length; i++) { //如果需要操作少一个桶，那么后面需要操作判断，即这里就说明了可以不操作最后一个桶
            l.add(new LinkedList());
        }

        //将元素根据区间放入桶中
        for (int i = 0; i < array.length; i++) {
            //根据公式，找到对应的下标
            int num = (int) ((array[i] - min) * (array.length - 1) / d); //进行取整，使得是那个下标
            //在前面我说过，这里必须要减1，因为我们也知道，他是在某个区间的桶比例，由于区间是少于数量的
            //比如1-2，2-3，3-4，4-5，明明是1，2，3，4，5这5个数，但是区间只有四个，所以这里实际上桶数量的确要减去1，但是又由于最大的值，必然是占用一个桶的，即需要包含最后一个，而不是省略他，而不省略他，因为下标的原因，必然是需要一个桶的，所以虽然说，桶数量与数组数量相同，又何尝不是因为区间的问题或者说下标的问题，导致出现最后一个桶呢，当然，你可以设置最后一个桶进行去掉，只需要下面的代码即可，认为他这个唯一也在倒数第二个桶里面，综上所述，因为区间的问题，所以真正的区间就是桶数量减去1
            //这里的注释：是留给前面少一个桶的，但是在解释中，我们也知道，要操作最大值，所以这里就注释了
//            if(num==l.size()){
//                System.out.println(1);
//                num--;
//            }
            l.get(num).add(array[i]); //将对应的数，放在对应的桶中
        }

        //每个桶都进行排序
        for (int i = 0; i < l.size(); i++) {
            //对集合元素进行排序（使用自然排序，一般是从小到大的，具体看对应添加的数据重写compareTo的方法）

            Collections.sort(l.get(i));
        }

        //进行打印
        double[] sortedArray = new double[array.length];
        int index = 0;
        for (LinkedList<Double> list : l) {
            for (double element : list) {
                sortedArray[index] = element;
                index++;
            }
        }
        System.out.print("[");
        for (int i = 0; i < sortedArray.length; i++) {
            if (i == sortedArray.length - 1) {
                System.out.println(sortedArray[i] + "]");

            } else {
                System.out.print(sortedArray[i] + ",");
            }
        }
    }

    public static void main(String[] args) {
        double[] array = {4.12, 6.421, 0.0023, 3.0, 2.123, 8.122, 4.12, 10.09};
        Sort(array);
        System.out.println("最大值是：" + array[array.length - 1]);
        array = new double[]{4.12, 6.421, 0.0023, 3.0, 2.123, 8.122, 4.12, 10.09};
        List<LinkedList<Double>> max = max(array);
        Array(max, array);
        //从这里可以看出，我们可以分开操作，那么就不用必须先排序，才可以得到最大值了，而可以先放好来直接得到最大值，所以在需求最大值时，比如单纯的不操作最后一个桶要方便许多，即时间复杂度要低
        //这就是为什么，多使用一个桶的原因
    }

    //上面基本是没有操作区间跨度，实际上因为具体程序的下标公式已经操作完成了
    //那么怎么去掉最后一个桶呢，答：再操作下标中，只要设置，判断即可，前面已经有了

    //那么为了进行方便取最大值，这里进行操作分开
    public static List<LinkedList<Double>> max(double[] array) {
        double max = array[0];
        double min = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
            if (array[i] < min) {
                min = array[i];
            }

        }

        double d = max - min;

        List<LinkedList<Double>> l = new ArrayList<>(array.length);

        for (int i = 0; i < array.length; i++) {
            l.add(new LinkedList());
        }

        //将元素根据区间放入桶中
        for (int i = 0; i < array.length; i++) {
            int num = (int) ((array[i] - min) * (array.length - 1) / d);
            l.get(num).add(array[i]);
        }
        System.out.println("最大值是：" + l.get(l.size() - 1).get(0));
        return l;
    }

    public static void Array(List<LinkedList<Double>> l, double[] array) {

        //每个桶都进行排序
        for (int i = 0; i < l.size(); i++) {
            //对集合元素进行排序（使用自然排序，一般是从小到大的，具体看对应添加的数据重写compareTo的方法）
            Collections.sort(l.get(i));
        }

        //进行打印
        double[] sortedArray = new double[array.length];
        int index = 0;
        for (LinkedList<Double> list : l) {
            for (double element : list) {
                sortedArray[index] = element;
                index++;
            }
        }
        System.out.print("[");
        for (int i = 0; i < sortedArray.length; i++) {
            if (i == sortedArray.length - 1) {
                System.out.println(sortedArray[i] + "]");

            } else {
                System.out.print(sortedArray[i] + ",");
            }
        }
    }
}

桶排序的时间复杂度是O（n），因为上面对应的操作基本都是操作对应数组长度的次数，也就是说，都省略的话，可以认为是O（n），而单看排序来说，实际上也的确只有n次，因为上面基本是平均的，也就是说，他们的结果实际上每个桶只有一次，所以是O（n），当然，实际上桶排序与快速排序有点类似，因为快速排序是先操作数据，然后局部操作区间，而这里直接的给数据给你了，然后操作区间，所以实际上桶排序节省了快速排序的交换（分开）次数（不是判断次数），也就是没有logn了，所以桶排序也能称为O（n），虽然这样说，基本是不正确的

实际上桶排序中，一般内部都会使用快速排序，但是，由于对应的进行了分配，所以除了比较次数外（因为比较只看长度，与是否分开无关，具体参考快速排序的n的解释），对应的logn中的n首先需要进行除以n（除以的n是桶的个数，也就是将分开的看成快速排序，只是对于整体而言，是除以n的个数），使得操作其对应的数据，即如果桶排序分配均匀，近似是O（n）了，否则如果除以的n是1，那么桶排序就是O（nlogn）了，除以的n是桶的数量，虽然最后一个桶一般只会占用一个，但也是占用了，当然不分配最后一个桶来除以n-1的话，也是近似O（n），因为差别不大，虽然可以使得除以的n变成很大，那么就比O（n）要小了，所以实际上桶的排序是平均起来是O（n），当然，也为了前面说的平衡，所以一般桶数量等于数组元素数量，这样就能最大限度的近似于O（n）了，这也是使用桶数量等于数组元素数量的一种原因

其实，我们可以定义链表大的在前面，所以由于整个数据是n，所以我们只需要判断链表的长度次数，那么实际上也是O（n），只是在输出时，是大的在前面了

但是对应使用的方法是Collections.sort，那么时间复杂度是多少呢，实际上他可以是O（n）（好像不确定，可以百度查看），注意该n只是当前所在的链表的元素个数，所以总体相加，那么就是O（n），该n代表数组长度

综上所述，桶排序的确是O（n），n是数组长度

各个排序比对表：

对于稳定性：冒泡的稳定解释已经说明了，快速之所以不稳定是因为对应的基准问题，实际上这里只会考虑相等的

由于对于的数据结构中，因为不相等的一般会操作false，所以冒泡由于不交换，所以稳定，快速由于不移动，所以不稳定（操作了相等的交换），堆由于不退出，使得交换父节点，所以不稳定，当然，他们都可以设置稳定，只是5总不能是大于5或者小于5吧，即认为稳定不考虑程序里面的相等的情况，或者说，自己解决的情况不算，因为快速可以设置>=进行right移动，使得5，4，5，中不会与5进行交换，所以导致可以稳定，而堆也可以设置>=，来使得退出，使得稳定，具体看对应代码即可

而由于计数和桶，因为只操作保存的数据，一般来说，如果是保存的数据，我们通常认为是有顺序的，所以他们都是稳定的

时间复杂度不用说明了，因为前面都已经说过了

那么现在我们说明空间复杂度，由于冒泡没有其他空间，只有赋值的空间，所以是O（1）

而快速排序由于没有增加数据时，都参与分开操作，所以实际上他的数据是针对与整体排序而言，是O（logn），即保证可以分开即可，而不必要添加相同长度的数组

堆排序也是一个数组，与冒泡一样，所以也是O（1）

计数排序，由于多出一个数组，所以是O（n），在程序里就是10，所以上面显示的就是程序里的

桶排序，由于需要创建桶，且认为桶的容量是数组的容量（保证防止越界，特别是数组），所以我们一般也会认为桶的空间复杂度是O（n）

注意，上面的空间复杂度代表的是提升，而不是总共，当然，就算是总共，由于省略，也就是提升了

至此排序操作完毕，实际上在硬件允许的情况下，我们可以来用空间换取时间（比如桶排序）

字符串匹配 ：

字符串匹配这个功能，是非常常见的功能，比如"Hello"里是否包含"el"

Java里用的是indexOf函数（后面有案例），其底层就是字符串匹配算法，主要分类如下：

案例：

package com.lagou;

/**
 *
 */
public class test11 {
    public static void main(String[] args) {
        System.out.println("hello".indexOf("el")); //1
        //即第一个e的位置，或者说，从下标1（字符串的下标）开始找到的
        //int indexOf(int ch)，用于返回当前字符串中参数ch指定的字符第一次出现的下标
    }
}

BF 算法：

BF 算法中的 BF 是 Brute Force 的缩写，中文叫作暴力匹配算法，也叫朴素匹配算法

这种算法的字符串匹配方式很"暴力"，当然也就会比较简单、好懂，但相应的性能也不高

比方说，我们在字符串 A 中查找字符串 B，那字符串 A 就是主串，字符串 B 就是模式串

我们在主串中，检查起始位置分别是 0、1、2…n，模式串长度是m，那么会操作n-m+1次，来看有没有跟模式串匹配的

这里是操作数量，也就是说，不会与前面的与起始数字情况公式有关（因为该公式是围绕下标的，所以该公式与下标有关，下标改变，他的结果也会改变，即通常需要换一种公式）

对应的代码，可以自己先进行操作：

package com.lagou;

/**
 *
 */
public class test22 {
    public static void main(String[] args) {
        String i = "hello";
        String k = "ll";
        for (int j = 0; j < i.length() - k.length() + 1; j++) {
            //循环就是来操作次数的，这里也刚好是对应的次数，那么既然是次数，如果j是<=，那么后面的+1可以去掉，这是程序里的，而不是数学里面的，程序满足数学即可

            //那么怎么匹配呢，很明显，我们需要取出对应的主串下标的对应值
            //String substring(int beginIndex, int endIndex)
            //返回字符串中从下标beginIndex（包括）开始到endIndex（不包括）结束的子字符串
            boolean equals = i.substring(j, k.length() + j).equals(k);
            if (equals == true) {
                System.out.println("下标在" + j + "位置找到");
                return;
            }
        }
        System.out.println("没有找到");
    }
}

时间复杂度：

我们每次都比对 m 个字符，要操作 n-m+1 次，所以，这种算法的最坏情况时间复杂度是 O（n*m）

m：为匹配串长度

n：为主串长度

实际上他也有最好的，比如（以完全不匹配为例子，因为运气好的话，自然都只需要一次即可，这里我们考虑完全不匹配，即最多的次数，所以在有些情况下，时间复杂度，有时候就是考虑最多的情况）：

n=1，m=1，那么就是1次

n=2，m=1或者2，那么就是2次

n=3，m=1或者3，就是3次，m=2就是4次

n=4，m=1或者4，就是4次，m=2或者3就是6次

很明显，在中间就是坏的情况，而两边就是好的情况，所以实际上最好的情况就是n，但是实际上，一般不会是两边，所以我们通常以m*（n-m+1）=n *m-m^2+m次来说明，一般来说，后面的可以省略，所以是O（n *m），当m是1或者n时，（不能省略，就是n了，如果省略，当m是n时，会变成n^2，这是错误的，所以不能省略，因为这里是对比操作了，对比1来说，对比不省略，实际上是计算，所以我们也说，计算也不操作省略，就如这里的n）

实际上当m是n时，若他不算对应的下标越界，还是可以变成n^2，但这并不理想，所以不会考虑，所以次数一般来说，我们直接计算出来，然后操作，从而不会导致越界

应用：

虽然BF算法效率不高但在实际情况下却很常用，因为：一般主串不会太长，实现简单

RK 算法 ：

RK 算法的全称叫 Rabin-Karp 算法，是由它的两位发明者 Rabin 和 Karp 的名字来命名的

BF算法每次检查主串与子串是否匹配，需要依次比对每个字符，所以 BF 算法的时间复杂度就比较高，是O（n*m）

我们对朴素的字符串匹配算法稍加改造，引入哈希算法，时间复杂度立刻就会降低

RK 算法的思路是这样的：我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值，然后逐个与模式 串的哈希值比较大小

如果某个子串的哈希值与模式串相等，那就说明对应的子串和模式串匹配了（这 里先不考虑哈希冲突的问题）

因为哈希值是一个数字，数字之间比较是否相等是非常快速的，所以模式串和子串比较的效率就提高了，而不用操作对比了

可以设计一个hash算法：

将字符串转化成整数，利用K进制的方式

比如：123的拆解，也就是1进制（0-9），十个数，如果包括0的话，10代表11个数，否则就是10，当然，一般我们都从0开始，且这些数字只是用来方便计算的，二进制也是从0开始，虽然在数学中我们默认从1开始的，但是在进制里实际上是从0开始，即99就是100个数了（包括0），而要跳到上一层的0，即需要加1，我们也可以认为从1开始，也就是说，将第一个认为是特例，这样也行（大多数都是这样）

我们将使用这个方式，100+20+3=123

现在开始，我们认为这样：

小写字母a-z：26进制

大小写字母a-Z：52进制

大小写字母+（0-9，即数字）：62进制

以只是小写字母的26进制为例

字符串"abc"转化成hash值的算法是：

a的ASCII码是97，b的ASCII码是98，c的ASCII码是99，正是因为他们的ASCII的值基本是不相同的，所以我们下面的计算方式基本是不会出现相同的，因为他的进制操作跨度比较大（即52，以及62，导致基本不会相同，当然如果都小于26也行，只要不是稍微大点即可，因为容易相同，逻辑思考一下就知道了，因为假设是3，4，那么3 * 4=4*3，很明显，他们一个乘以4，一个是3，4只比3大一点，所以有相等的可能，而如果3去乘的数比乘的4大很多，或者比乘的3小，那么基本不会相同）

那么可以不乘以进制数吗，当然不行，进制数是为了保证位置的，否则cb和bc的结果必然是相同的，但他们却不是相同的字符串

因为若主串是bc，那么cb是不能匹配成功的，再次举例：ad也会等于bc，因为他们相加都是197，所以我们需要进制来保证位置

那么有个问题，上面的进制是跨度足够比较大吗，实际上需要这样的考虑，考虑A和z，A是65，z是122，在上面说的，我们需要考虑最小和最大的界限，比如AA=6552+65，ZZ=90 * 52+90，而aa=97 * 26+97，zz=12226+97，我们直接的比较，ZZ=4770，aa=2619，AA=3445，zz=3269，很明显，26的次方的最大值，都比52次方的最小值要小，所以他们不会相同，而52若再小点，就不一定了，即得出结论，52的跨度足够大，所以自定义的52可以使用

注意对应的方法可不是二进制的操作，即不是9*26^1+7 *26^0，这样的操作，他只是直接的乘，这就是K进制的方式

上面的结果是：65572+2548+99=68219

字符串"abc"转化成hash值是68219

一般情况下，97是当前主串和从串的最小数字，当然，中间也行，因为负数也不会相同，负数只是操作反向的数字而已，所以也是不会相同的，因为他们的差还是一样的（即不会为0，即不会相同，所以52还是可以）

字符串"abc"转化成hash值的算法是：

0+26+2=28，这样就能减少很多的计算

现在我们来进行实现（可以自己先操作一下）：

package com.lagou;

/**
 *
 */
public class test33 {

    //首先我们先考虑26进制的计算方式，这里进行编写方法
    public static int strToHash(String s) {
        int hash = 0;
        for (int i = 0; i < s.length(); i++) {
            hash *= 26; //为什么放在前面，因为位数的问题，所以放在前面，可以自己选择思考就知道了，假设是abc，那么a应该是26^2，而放在前面就可以解决
            hash += (s.charAt(i) - 97); //减97节省计算，操作运算时，会字符会变成对应的int类型的数字的
        }
        return hash;
    }

    //我们的哈希值操作完毕，现在编写方法
    public static void is(String s, String b) {
        //首先我们先拿取对应的字串（模式串，匹配串）哈希值
        int i = strToHash(b);

        for (int j = 0; j < s.length() - b.length() + 1; j++) {
            if (strToHash(s.substring(j, b.length() + j)) == i) {
                //到这里，说明哈希值相等，那么就匹配到了
                System.out.println("匹配成功，下标是：" + j);
                return;
            }
        }
        System.out.println("没有找到");
        
        //实际上substring不能超过其下标上限，否则报错，但是由于j < s.length() - b.length() + 1;的原因，使得如果模式串大于主串，自然是不会操作循环的，也就是直接的退出，所以基本不会报错

    }

    public static void main(String[] args) {
        is("avfg", "fg");
    }
}

我们可以看到，只需要对应的n-m+1次就行，如果m=1，那么就是n次，如果m=n，那么只需要1次，即平均我们可以认为是O（n），而不是之前的O（n*m）了，即这里最坏的情况就是O（n），也就是m=1的时候（最后一个获取，时间复杂度，在没有明确次数时，默认考虑最多的情况，而不是靠运气）

至此，时间复杂度我们变成了O（n）了，n代表对应的次数（n-m+1），比单纯的n要少次数的

注意：这里是没有考虑哈希算法的计算的时间复杂度的，所以要注意

说到时间复杂度考虑最多的情况，好像之前的我们都没有这样说明，这里来补充，实际上之前的都只是操作数据结构，而数据结构，无论是数组还是链表，还是他们组成的操作，实际上与具体次数没有关系，只是他们的结构操作关系，所以最多和最少是没有任何说明的，那么实际上最多和最少，是体现在查找中，也就是说，无论是之前的查找，还是现在的查找，我们都按最多来计算，数据结构自然也是如此，因为只有查找基本才需要运气成分

时间复杂度：

RK 算法的的时间复杂度为O（n+m），上面不是说O（n），为什么这里需要加上m，这是因为考虑hash算法的存在（注意，哈希算法在代码里面实际上不要考虑，因为一般的哈希算法都是O（1），只是这里我们操作了自定义的，如果非要考虑，那么实际上String的哈希函数操作也是循环，但实际上只会认为是O（1），因为他是基础底层的原因，而在前面我们说过，时间复杂度，只是操作具体的明面上的次数，而不是基础底层的次数，所以哈希算法我们一般认为是O（1），前面说明过了，在时间复杂度的说明那里，如果这里在考虑循环是m的情况下，即也是n *m-m^2+m，但是由于要比原来的要多一个m，因为外面有一个循环，即是n * m-m^2+2m，所以实际上考虑，整体是要差的），导致的，这里我们就只考虑外面的循环，所以需要加上m，那么我们来分析一下具体优化是什么，现在我们来操作对比，所以不能省略：

之前的是n *m-m^2+m，n代表主串长度，m代表字串长度

现在的是：n-m+1+m，即n-m+1+m，n代表主串长度，m代表字串长度，这里只考虑外面的了

我们可以发现，如果m是1，那么之前的是n，现在的是n+1，m是n时，之前的是n，现在的是n+1，即之前的好，如果m>1或者m<n，那么现在的好，所以总体来说，现在的比之前的要好很多，特别是m越来越大的情况，我们看上面的时间复杂度，所以也可以得出是O（n+m），比O（n*m），要好，极端情况下要差，比如m=1或者m=n（因为我计算了对应的哈希值，且他也是直接的对比），其他情况，我一次计算哈希值，顶掉其他的所有次数，当然，由于是看整体，且基本m不会等于1或者n，所以这里整体要好

应用：

适用于匹配串类型不多的情况，比如：字母、数字或字母加数字的组合，以及"大小写字母+数字"（比如前面说明的62进制方式的操作），因为其他的类型，可能会导致计算结果过大，并且没有明确的类似的表ASCII，就算有，因为数字很大（对应的标识，就如a是97，特别是汉字，比如汉字"哈"就是21644，有点大了），也不建议使用

BM 算法：

BF 算法性能会退化的比较严重，而 RK 算法需要用到哈希算法，而设计一个可以应对各种类型字符的哈希算法并不简单，比如上面说明的汉字，在操作后续的计算时，可能计算的结果会非常大，不好保存和计算，就算使用BigInteger来保存，但是因为计算量太大了，所以会导致比较慢，所以这种情况下，并不友好

那么现在我们来操作另外一种算法：

BM（Boyer-Moore）算法，它是一种非常高效的字符串匹配算法，滑动算法

在这个例子里，主串中的 c，在模式串中是不存在的，所以，模式串向后滑动的时候，只要 c 与模式串有重合，肯定无法匹配

所以，我们可以一次性把模式串往后多滑动几位，把模式串移动到 c 的后面

BM 算法，本质上其实就是在寻找这种规律，借助这种规律，在模式串与主串匹配的过程中，当模式串和主串某个字符不匹配的时候，能够跳过一些肯定不会匹配的情况，将模式串往后多滑动几位，从而减少次数

算法原理：

BM 算法包含两部分，分别是坏字符规则（bad character rule）和好后缀规则（good suffix shift）

坏字符规则：

BM 算法的匹配顺序比较特别，它是按照模式串下标从大到小的顺序，倒着匹配的，那么可不可以正着匹配，答：最好不可以，后面会说明情况，当然，这里代表的不是下标，而是匹配的顺序，不要以为是下标，如下图：

我们从模式串的末尾往前倒着匹配，当我们发现某个字符没法匹配的时候，我们把这个没有匹配的字符叫作坏字符（主串中的字符），如下图：

字符 c 与模式串中的任何字符都不可能匹配，这个时候，我们可以将模式串直接往后滑动三位，将模式串滑动到 c 后面的位置，再从模式串的末尾字符开始比较，如下图：

坏字符 a （是对应主串的a哦）在模式串中是存在的，模式串中下标是 0 的位置也是字符 a，这种情况下，我们可以将模式串往后滑动两位，让两个 a 上下对齐，然后再从模式串的末尾字符开始，重新匹配，如下图：

注意：上面的a在模式串中是第一个a，也就是说，如果是aabd，那么就是第二个a，因为他的acabd可能是aaabd，那么这样才能保证是可以匹配的，那么从这里可以发现，如果我们是正向的操作，你必须循环模式串（一般是坏字符前面的，在程序里会操作说明的），因为你不能保证该模式串的后面是否还有a，所以我们需要反向的进行操作，主要是为了，刚好找到第一个a即可确定下标来移动，实际上坏字符也是这样，可以使得第一个就是坏字符，而不用全部进行匹配，总而言之，我们使用反方向比正方向要方便许多

当发生不匹配的时候（出现坏字符，那么就是不匹配，这里可没有直接的哈希对比和直接对比，参考前面两个操作即可，一个使用哈希的就是哈希对比，没有使用的就是直接对比，后面会说明为什么不使用哈希对比），我们把坏字符对应的模式串中的字符下标记作 si，如果坏字符在模式串中存在， 我们把这个坏字符在模式串中的下标记作 xi，如果不存在，我们把 xi 记作 -1（代表直接的过去），否则减去xi，代表他们需要移动多少距离，使得刚好对上，那么模式串往后移动的位数就等于 si-xi（下标，都是字符在模式串的下标），如下图：

举例：

第一次

c在模式串中不存在，由于c在模式串中是第二个下标，所以si=2，因为不存在，所以xi=-1，那么结果就是2-（-1）=3，移动3位

所以第一次移动3位

第二次：

a在模式串中存在，所以 xi=0，移动位数是2-0=2，即移动2位

所以第二次移动2位

好后缀规则：

如下图：

从上图看出，坏字符后面还有已经匹配的，我们把已经匹配的在模式串中查找，如果找到了另一个跟主串{u}（主串或者字串的部分串，简称部分串）相匹配的子串{u}，那我们就将模式串滑动到子串{u}与主串中{u}对齐的位置，如下图：

很明显，如果只看坏字符的话，他只会移动一次，而这里直接的跳过坏字符移动了，因为既然出现了坏字符，那么若没有找到对应的{u}，即前面实际上也不要进行判断匹配的，所以直接的忽略坏字符

如果在模式串中找不到另一个等于主串{u}的子串，且这时不匹配，我们就直接将模式串，滑动到主串中{u}的后面，因为之前的任何一次往后滑动，都会没有匹配主串中{u}的情况，也就必然不会成功，如下图：

过度滑动情况，如下图：

因为上面的主串{u}是两个，那么当只需要一个时，是不用继续滑动的，所以如果还是直接的在后面，那么会产生过度的滑动，所以这时不应该滑动了

简单来说：

当模式串滑动到自身前缀（前面的模式串的字串，一般是主串{u}大小减1，就是前缀的大小的范围，这里只有1，所以前缀是1，否则如果有2的话，那么该前缀可以是2，或者1）与主串中{u}的后缀（只有1，如果有2的话，可以是2或者1）有部分重合的时候，并且重合的部分相等的时候，就有可能会存在完全匹配的情况

因为之前的都是匹配两个，可没有匹配一个的，所以这里需要注意

所以，针对这种情况，我们不仅要看好主串{u}在模式串中，是否有另一个匹配的子串{u}，我们还要考察好主串{u}的后缀子串（c），是否存在跟模式串的前缀子串（c）匹配

如何选择坏字符和好后缀：

我们可以分别计算好后缀和坏字符往后滑动的位数，然后取两个数中最大的，作为模式串往后滑动的位数，比如前面的图片中，坏字符只需要移动1为，而好后缀却需要移动3位，所以我们以好后缀为主

因为他们都是一种操作，只要有一个不会匹配，必然是移动最大的，因为就算移动最小的，必然也会匹配失败，因为没有满足另外一个大的移动，而我们操作大的移动，自然会使得更少的操作执行次数

算法实现：

这里先主要说明坏字符：

如果我们拿坏字符，在模式串中顺序遍历查找，这样就会比较低效，在这之前，那么有个问题，坏字符他本身的移动次数对比之前的移动（哈希对比）来说会不会提高总次数吗，答，实际上会

那么又有一个问题，坏字符可以使用哈希对比吗，答：最好不要，因为我们知道，坏字符会进行匹配模式串，也就是说，他需要进行循环操作对比，所以使用哈希对比没有什么作用

现在举个例子：

假设你的主串是abcdaba，模式串是aba，首先我们匹配一开始是不成功的，如果不使用坏字符，需要1次（哈希值），不考虑外面的3次（哈希方法），那么需要移动4次（匹配后移动，所以是包含的，记得结合程序来看），才可以匹配到，然后1次匹配成功，总共4+1=5次（认为对应的哈希是1次的，否则就是3+5 * 3=18次了，不考虑外面的就是15次，而不使用哈希的那么就是7-3+1=5，5*3=15次），而使用坏字符，那么他就不会像我们移动并慢慢的都进行匹配，他先从后面开始匹配，如果直接不成功，那么前面的也就不需要匹配了，所以很明显，他减少了次数，那么他一开始就是1次，但是需要看看是否有相同的，那么也会浪费3次（包括该一次），即总共3次（注意我们说明的都是循环的次数，循环的操作有多个，我们统称为1次，循环里面的循环的次数我们也算），当他直接到dab时，由于最后也是不相同，浪费1次，但是他模式串最后一个是b，在模式串中是可以找到的，那么就会操作2次（包含该1次），然后移动，最后1次，进行3次匹配，使得匹配成功（不是哈希），总共有3+2+3=8次，自然比5次需要更多次数，所以实际上会提高总次数，但是如果按照程序来算的话，8是远远的小于18和15的，所以坏字符大大提高了执行效率（因为我们会根据理论来进行跳跃，而他们却傻傻的移动一步，使得虽然相同的次数，但是没有跳跃的都操作了，使得高两个3，一个2，这里更加的有好处），但是对于哈希算法是O（1）来说是降低的，以后以哈希算法是O（1）这个为主

这里就回到了上面的说明"如果我们拿坏字符，在模式串中顺序遍历查找，这样就会比较低效"，这就是原因，即这里我们需要解决对应的遍历查找问题，因为这里占用了3+2=5次的遍历，而哈希值，是直接的匹配成功，我们仔细的观察，实际上他的遍历在某些情况下会多一次，也就是2次的那个地方，因为他的移动需要找到是否相同的来决定，而没有不相同的与单纯的移动是一样的（对于哈希是O（1）来说），所以整体来说，遍历的次数必然大于等于单纯的移动，但是该2次的地方实际上只会增加一次，也就是说，只有一次只差，那么如何解决呢：

我们可以采用散列表，我们可以用一个256数组，来记录每个字符在模式串中的位置，数组下标可以直接对应字符的ASCII码值，数组的值为字符在模式串中的位置，没有的记为-1

也就是说，用他们本身数字的哈希值来操作下标，那么如果主串对应的坏字符在数组里有，只需要去数组里找即可，若返回了对应下标的值（该值是该字符在模式串的下标），那么就说明找到了，而没有返回自然就是-1（-1使得可以直接的移动模式串长度，所以默认为-1），我们简称他为哈希对标，或者哈希对比下标

比如bc[97]=a（也就是3），bc[98]=b（也就是1），bc[100]=d（也就是2），很明显，可以通过坏字符来找到对应的模式串的下标，当然有重复的字母以后面的位置为准（这里是有问题的，在后面会进行解决，程序里会进行说明），即当我们保存时，从第一个保存，那么最后面的自然会操作覆盖，所以也就是使得找到其最后一个，那么你可能会认为256长度的数组，难道不会导致空间过大吗，答：这种想法是正确的，但是你要知道，字符是非常多的，如果不设置非常大的数组，那么可能有些字符保存不了，即出现越界，特别是汉字，当然，汉字我们一般不会操作，所以总体来说，256刚刚好了，当然这里只是测试，你完全可以自己设置少点的空间

那么有个问题，使用这个，可不可以使用哈希对比（前面的哈希操作，是自定义的那个地方）来直接匹配了，答：与前面说的"答：最好不要"不一样，前面由于我们需要利用自身来移动（与自身匹配，来得到坏字符），那么自然不会只移动一位，所以不会有多余的操作（哈希值），并且，我们也知道，实际上这样的判断是可以等于单纯的移动的，只是有些情况会大于，如前面的2次，那么如果操作了这里，很明显，都只需要一次即可，即前面的总次数就是1+1+3=5次了，即比原来的5次相同了（注意：是在好的案例的情况下，特殊的案例在程序里会说明，如果包含特殊案例，我们可以认为是等价的），当然，如果主串或者模式串很长，那么我坏字符自然要比原来的匹配要好，因为我一次就能移动很多次，如果是刚好匹配，那么他不会出现坏字符，那么这些操作也就没有作用，根据这里来说，因为我们可以一次性的就能知道是否存在，所以到那时，可以来操作哈希，即加上哈希，那么每次之前都会进行哈希操作，默认为O（1），这样就能看看是否先匹配了

但是我们不会这样，虽然与前面的不一样，但也只是判断是否存在不一样而已，实际上都需要判断是否有坏字符，那么在这种情况下，必然是需要循环的，所以这个循环可以利用，如果加上了哈希，如果该最后一次循环的次数比总体的哈希次数要少，最好直接的不加上哈希，否则可以加，但是主串越长的情况下，使用哈希越不好，因为其他的次数都需要哈希，如果模式串很长的话，使用哈希好点，因为不用判断是否有坏字符了，所以我们可以认为他们是平等的，但是使用哈希需要代码量，那么使用哈希要差点，所以就不使用哈希了（即哈希对比）

现在我们先来完成坏字符，然后在坏字符中进行修改，使得加上好后缀，并且，这里我会给出如果使用正方向的话，对应的缺点的地方是什么（也就是在那个位置给出解释），这里你可以先看一下然后自己编写试一试：

package com.lagou;

/**
 *
 */
public class test44 {

    //操作模式串的哈希保存
    //参数1，要保存的模式串
    //参数2：要保存的位置数组
    public static void generateBC(String b, int[] dc) {
        //我们知道，如果对应坏字符不存在，需要是-1，所以需要将对应的数组都设置为-1
        for (int i = 0; i < dc.length; i++) {
            dc[i] = -1;
        }
        //设置好-1后，我们需要进行操作对应的下标进行放入，即放入自身的ASCII的值当下标，使得唯一，然该下标位置放入自己的所在模式串的下标
        for (int i = 0; i < b.length(); i++) {
            dc[b.charAt(i)] = i; //charAt虽然得到的是字符，但是在与int操作时（比如赋值或者计算等等），会变成对应的ASCII值的
        }
        //这样我们就保存好了


    }


    //要操作坏字符，首先我们定义一个方法
    public static void bad(String a, String b) {

        //定义数组
        int[] array = new int[256]; //设置256是保证字符可以保存其下标
        generateBC(b, array);
        //这里要说明一下：二维数组的创建有点不对称，但是这是规定，所以不用理会
        /*
        因为int[] a = new int  [256]
         int[][] a = new int[][256] 这个是错误的，所以我才说不对称，实际上二维数组不能这样的说明我们要将int[][]看成是整个名称，而数组长度只写在前面括号，那么就说的通了
         

 这里还需要考虑一个问题：
 如果是这样的例子，怎么操作
        acvvfdvf
        vfdvf
         */
        //很明显，他找的是d前面的v，但是由于我们是保存最后一个，所以如果相减，自然为-1，而-1会导致往前移动，那么又会坏字符，并且可以找到，且v为4
        //那么4-4=0，可以发现又回来了，导致无限循环，因为对应的i才是为主，我们移动的只是i的值而已，所以这里需要考虑该问题
        //即如果坏字符一开始就找到了，那么我们可以使用哈希值来直接的找到，否则，我们最好还是进行遍历（总不能再次的操作空间吧，后面会给出代码来操作），那么有个问题，在中间的坏字符会与前面的2次的那个地方是一样的吗，答：不是一样的
        //因为他的坏字符后面的已经也操作了判断，所以导致实际上多出几次，比如这里就多出2次，也就是说，这里操作判断了5次，却只移动2次，所以在原来的基础上，本来是多一次的，但是却又多了两次，所以不一样
        //那么总体来说是好还是坏呢：
        //那就要看实际情况了，如果模式串是10个，那么我可以使用1次来完成10次，少9次，但是他也有对应的9次会使得多9次，那么总体来说是相同的，所以我们认为，单纯的坏字符与普通的哈希对比是等价的（认为我们定义的哈希对比是O（1），否则是大大提高的，前面已经说明过了）

        //现在我们来操作循环，这里我们默认还是一样的次数，因为他最多也是这样的次数
        for (int i = 0; i < a.length() - b.length() + 1; ) {

            int j = 0;
            //我们来看看对应是否有坏字符
            for (j = b.length() - 1; j >= 0; j--) {
                if (a.charAt(j + i) != b.charAt(j)) { //如果是字符，直接的等于即可
                    break;
                    //既然不会相等，那么说明没有匹配成功，因为有坏字符
                    //那么如果都退出呢，怎么在循环中进行退出呢，实际上这里我们可以将j定义在外面，那么可以退出了
                    //并且也可以再次的使用
                }
            }
            if (j < 0) { //设置小于是防止特殊情况，虽然这里不会出现
                System.out.println("匹配成功，下标是：" + i);
                return;
            }
            int ii = 0;
            if (j != b.length() - 1) {
                char c = a.charAt(j + i);
                //到这里说明坏字符不是最后一个，那么操作遍历，这里也包含了一种特殊的情况，如果没有前一个（也就是在坏字符中没有坏字符前面的字符），也就是说，j-1中j是0，那么他会直接的退出，并且ii=-1.所以也会使得加上1（-（-1））的下标，也正好进行了移动
                //所以这里也包括了直接退出的情况，所以就不用考虑直接退出的情况了
                for (ii = j - 1; ii >= 0; ii--) {
                    if (b.charAt(ii) == c) {
                        break;
                    }
                }
            }


            //这里就要考虑对应的坏字符是否存在的问题了，这里可以直接的计算，使用公式，也就是之前的si-xi
            //si是模式串坏字符对应下标，也就是j，xi是对应坏字符存在的下标，也就是array[a.charAt(j+i)]
            //即找到对应主串坏字符是否在数组中存在，而j+i代表在主串对应的坏字符的下标，得到该坏字符，我们使用他的ASCII去找数组的值来获得下标
            //那么结果就是j-array[a.charAt(j+i)]，就是移动的次数了

            //因为有坏字符，那么我们进行对应的移动
            if (j == b.length() - 1) {
                i += j - array[a.charAt(j + i)];
            } else {
                //坏字符在中间
                i += j - ii;
            }
            //移动后，自然也会进行重新操作的

        }

        //如果都没有匹配成功，那么自然匹配失败
        System.out.println("没有找到");
    }

    //如果可以的话，实际上这里可以操作数组，只是赋值是反向赋值即可，并且找到相同的就不操作赋值，这样，后面的代码就不用判断了
//也就是上面注释说过的"总不能再次的操作空间吧，后面会给出代码来操作"
    //代码如下：

    public static void generateBC11(int[] dc) {

        for (int i = 0; i < dc.length; i++) {
            dc[i] = -1;
        }


    }

    public static void generateBC12(String b, int[] dc, char v) {

        for (int i = b.length() - 1; i >= 0; i--) {
            if (b.charAt(i) == v) {
                dc[v] = i;
                break;
            }

        }


    }

    public static void badd(String a, String b) {
        int[] array = new int[256];
        generateBC11(array);

        for (int i = 0; i < a.length() - b.length() + 1; ) {

            int j = 0;

            for (j = b.length() - 1; j >= 0; j--) {
                if (a.charAt(j + i) != b.charAt(j)) {
                    break;

                }
            }
            if (j < 0) {
                System.out.println("匹配成功，下标是：" + i);
                return;
            }


            String c = b.substring(0, j);
            generateBC12(c, array, a.charAt(j + i));

            //通过其方法可以看到，实际上与遍历是一样的，所以说使用这种也行，次数也与遍历（包括先保存的）加上总遍历是基本是等价的（特殊的方法）
            //但是该情况又何尝不是没有使用哈希对比下标之前的坏字符吗，只是遍历使用数组保存而已，所以总体来说
            //我们会使用第一种情况（即先都保存，然后遍历，即上面的bad方法，badd是第二种情况，没有操作哈希的，我们可以认为是第三种情况，虽然这里没有说明，因为总不能所有情况都写上吧，所以从这里开始，我们只会选择主要的情况来操作，并且也选择方便操作来操作了）
            //这两种你可以随便使用其中一种，这里我们就操作第一种，因为第一种在坏字符是最后的情况下，执行的代码是少的，其他时候，基本差不多，所以第一种好丢丢


            i += j - array[a.charAt(j + i)];
            if (i + j <= a.length() - 1) {
                array[a.charAt(j + i)] = -1; //重新变回原来的样子，否则会使得没有赋值退出时，认为还存在，特别是截取的字符串是""的时候
            }

        }


        System.out.println("没有找到");
    }


    //我们可以看到，我们操作的基本的坏字符查询实际上并没有什么明显的提升，因为是等价的，在有些情况下可以一下子找到，有些情况下难找一点，总体等价
    //现在我们来进行扩展使得加上好后缀


    public static void bad1(String a, String b) {

        int[] array = new int[256];
        generateBC(b, array);


        //加上好后缀
        //因为好后缀的原因，那么他必然会使得坏字符到中间，我们继续看后面代码的解释

        for (int i = 0; i < a.length() - b.length() + 1; ) { //后面需要加上;，否则报错，这是java的结束符，不要忘记了
            int j = 0;
            for (j = b.length() - 1; j >= 0; j--) {

                if (a.charAt(j + i) != b.charAt(j)) {
                    break;

                }


            }


            if (j < 0) {
                System.out.println("匹配成功，下标是：" + i);
                return;
            }

            int ii = 0;
            if (j != b.length() - 1) {
                char c = a.charAt(j + i);
                //到这里说明坏字符不是最后一个，那么操作遍历
                for (ii = j - 1; ii >= 0; ii--) {
                    if (b.charAt(ii) == c) {
                        break;
                    }
                }
            }

            //接着上面的问题，我们先操作如下：
            //这里要考虑移动谁了
            //首先我们得到坏字符的移动次数
            int aa;
            boolean is = true;
            if (j == b.length() - 1) {
                aa = j - array[a.charAt(j + i)];
                is = false; //代表，没有好后缀
            } else {
                //坏字符在中间
                aa = j - ii;
            }
            //然后得到好后缀的移动次数
            //但是好后缀的移动次数在前面并没有说明，现在我们来思考一下，公式是什么
            //首先给出例子：
            /*
            acvvfdv
            vfdvf
             */
            //我们可以知道，后面两个vf是相等的，那么通过上面的程序，应该找到前面的vf
            //很明显，这里需要移动3次，而坏字符移动2次，所以我们应该是移动3次
            //但是我们需要考虑过度滑动的情况
            //但首先，我们先不考虑过度的滑动，我们先将该3次进行计算出来，我们可以很明显的发现，他移动的次数，是其中最后一个v下标减去前一个v下标，也就是3-0=3
            //但是前一个v需要保证其后面的与原来匹配好的好后缀一致，所以这里要注意，后面会有举例
            //那么有个问题，我们需要考虑是否存在好后缀呢，答，要考虑
            /*
            举例：
            dfgh
            fg
            如果我们不考虑好后缀是否存在，那么由于g只会存在一个，考虑普通的移动，也就使得1-（-1）=2了，那么就跳过了正确的匹配（结合代码，要移动两次），当然真正的这里的代码，即在下面的代码中，会导致越界
            比如：
             for (int kk = j - (b.length()-1 - j - 1); kk >= 0; kk--) {
                //判断算法相同的起点
                if (b.charAt(kk) == b.charAt(j + 1)) { 这个b.charAt(kk) 会越界，因为上面的kk比原来的j要大了，导致越界了
            所以需要进行判断是否存在好后缀

             */
            //这里我们直接以坏字符为主即可（后面的if中的>=）
            /*
            同样的，他这里也只会保存后两个字符，所以如果出现这种情况也是不行的：
            acvvfvvfdvfv
            vfdvfv
            即坏字符在模式串的d中，由于坏字符我们已经操作过了，他不会有问题，但是好后缀怎么办呢，很明显，这里应该要跳过，也就是说，在保证找到第一个v时，也要保证后面相同
             */

            //现在我们来操作
            //我们如何确定好后缀的下标呢，实际上j+1就是对应的好后缀的起始的下标，前提是，怎么操作第二个整体好后缀（比如举例的dgg）
            //那么只能操作循环了
            //次数是：
            /*
            举例：
            wertddfdggsas
            weftdggdgg
            很明显，我们应该需要从坏字符那里的g的前面一个d开始，那么很明显，就是坏字符下标减去2，而这个2，就是模式串的最大下标减去坏字符下标再减1
             */
            int bb = 0;
            if (is == true) {
                //定义找到的下标，如果没有找到，那么默认为模式串的长度
                int gg = b.length();

                for (int kk = j - (b.length() - 1 - j - 1); kk >= 0; kk--) {
                    //判断算法相同的起点
                    if (b.charAt(kk) == b.charAt(j + 1)) {
                        //定义退出变量
                        int oo = 0;
                        //现在我们开始判断后面的是否相同，但在之前，首先看看有没有后面的字符
                        //如果下面的循环直接的退出，自然就代表没有后面的字符

                        for (int pp = 1; pp < b.length() - 1 - j - 1; pp++) { //根据例子来说，只需要对应的两次即可
                            if (b.charAt(pp) != b.charAt(j + 1 + pp)) {
                                oo = 1;
                                break;
                            }
                        }
                        if (oo == 0) {
                            gg = kk;
                        }

                    }

                }
                int p = gg;
                //这里来操作一下过度滑动的判断，我们只需要看看最前两个中（上面的例子），是否在匹配好的中有对应相同的字符
                if (gg == b.length()) {
                    int tt = 0;
                    //这里也是b.length() - 1 - j-1，因为起始的都没有匹配，那么就不需要匹配了
                    for (int ll = b.length() - 1 - j - 1, jj = 1; ll > 0; ll--, jj++) { //执行对应次数
                        if (b.charAt(0) == b.charAt(j + 1 + ll)) {
                            tt = jj;
                        }
                    }
                    gg -= tt;
                }
                if (p == b.length()) {
                    bb = gg;
                } else {
                    bb = j + 1 - gg;
                }
            }
            if (aa >= bb) {
                i += aa;
            } else {
                i += bb;
            }


        }

        System.out.println("没有找到");
    }

    //我们可以看到，使用好后缀，使用了非常多的代码，判断了很多次，在前面，坏字符操作中间时，他多出了对应的好后缀的次数，而这里在该次数上，一般也多出了很多次，即原来是等价的，但是现在多了对应的次数了，该次数最少是好后缀减1（因为过度），最多是前面第一个判断是否有相同后缀的好后缀，即：（好后缀/总好后缀）*（模式串长度），由于出现的起始数量是随机的，那么根据大致平均，我们可以认为他与坏字符等价（包括前面多余的2次好后缀以及过度），即我们可以认为，在坏字符的基础次数上，认为加上和坏字符的次数即可，即原来的等价，现在加上了同样的等价
    //也就是说，该BM算法（好后缀）很极端，慢的很慢，快的很快，虽然坏字符也是如此，所以虽然在一般小的模式字符串使用BM算法好，即他的慢自然也是O（n+m），因为在等价的基础上，加上了对应模式串的次数
    //这里我们以快的为准，如果是最快的，那么很明显，就是一次性得到，这里我们忽略一开始的创建数组（因为数组是可以被很多人利用的，所以我们可以忽略）
    //即空间换取时间
    //那么我们以坏字符为例，如果始终是最后一个是坏的字符，那么就是n/m了，而好后缀可以使得，就算是中间的坏字符，那么若始终没有其他的好后缀的后面字符，那么也可以是n/m，虽然他可能会提高次数，但是，只是最高的水平，而纵观全局，实际上要提高很多次数的（坏字符也是，他们是等价的），即若在极端的情况下，因为每次都是移动模式串的大小，即这是最快的情况，所以在极端情况下，我们一般会称BM的时间复杂度是O（n/m）
    //否则平常我们可能会认为是O（n+m），因为等价下，又会加上好后缀的次数（即m，虽然是等价，但是并非是相同的，即等价只是时间复杂度是类似的而已）
    //并且，好后缀和坏字符的程序，如果没有好的优化的话，建议不要结合来使用，因为虽然极端情况下，会使得找的很快，但大多数是慢的，因为他们的时间复杂度是相加的（除非你找的字符很少，因为很少的模式串，极端情况容易出现，使得他们的判断可能因为其中一个而直接的跳过，比如坏字符在最后面，那么没有好后缀，那么好后缀就会跳过，在程序里已经操作了），但实际上好后缀和坏字符也能自己来操作，那么可以说，那么他们只需要他自身的长度的次数
    //所以在不建议结合来使用，是因为有些情况好后缀好，有些情况坏字符好，比如dffggghhh，模式串是gff，那么坏字符只会移动一次，而好后缀直接移动3次
    //但若模式串是vffggdh，那么坏字符直接移动6次，而好后缀却只移动1次，所以他们各有优势
    //而结合的话，就没有优势了（因为都操作了对应代码，即时间复杂度相加了），因为没有人可以同时操作两个，所以这里就需要看使用者的选择了，就如数组和链表一样，总得选择一个吧，总不能都放在一起，都来使用或者操作吧，当然，这里给出了对应的结合代码，以及分开的代码，根据上面的介绍，所以我们尽量操作分开的

    //至此，坏字符和好后缀说明完成，注意：这里是结合当前代码来分析的，如果理论不准确，或者时间复杂度不对，那么就是说明程序还可以优化
    //现在以坏字符为主，看看正方向的操作是否不好
    public static void bad2(String a, String b) {


        int[] array = new int[256];
        generateBC(b, array);


        for (int i = 0; i < a.length() - b.length() + 1; ) {

            int j = 0;
            //要验证操作正向的，这里需要改变吗，答：这里不需要，因为他只是从最后开始进行判断是否相同的而已
            for (j = b.length() - 1; j >= 0; j--) {
                if (a.charAt(j + i) != b.charAt(j)) {
                    break;

                }
            }


            if (j < 0) {
                System.out.println("匹配成功，下标是：" + i);
                return;
            }
            //这里才是真正的验证正方向的地方
//            int ii = 0;
//            if (j != b.length() - 1) {
//                char c = a.charAt(j + i);
//
//                for (ii = j - 1; ii >= 0; ii--) {
//                    if (b.charAt(ii) == c) {
//                        break;
//                    }
//                }
//            }
            int ii = 0;
            if (j != b.length() - 1) {
                char c = a.charAt(j + i);
                for (int iii = 0; iii <= j - 1; iii++) {
                    if (b.charAt(iii) == c) {
                        ii = iii;
                    }
                }
                //需要判断没有操作循环的情况，也就是在坏字符中没有坏字符前面的字符（前面说明过了）
                if (j == 0) {
                    ii = -1;
                }
                //当遍历结束后，那么自然得到的就是最终的下标，也就是ii，很明显，他需要都进行遍历，没有break，所以我们才说，正方向比反方向不好，因为正方向不能确定他是否是最后一个该字符，所以需要都进行循环
            }


            if (j == b.length() - 1) {
                i += j - array[a.charAt(j + i)];
            } else {
                i += j - ii;
            }

        }

        System.out.println("没有找到");
    }

    //单纯的好后缀操作
    public static void bad3(String a, String b) {

        int[] array = new int[256];
        generateBC(b, array);

        for (int i = 0; i < a.length() - b.length() + 1; ) {
            int j = 0;
            for (j = b.length() - 1; j >= 0; j--) {
                if (a.charAt(j + i) != b.charAt(j)) {
                    break;

                }
            }

            if (j < 0) {
                System.out.println("匹配成功，下标是：" + i);
                return;
            }
            boolean is = true;
            if (j == b.length() - 1) {
                is = false;
            }
            int bb = 0;
            if (is == true) {

                int gg = b.length();

                for (int kk = j - (b.length() - 1 - j - 1); kk >= 0; kk--) {

                    if (b.charAt(kk) == b.charAt(j + 1)) {

                        int oo = 0;


                        for (int pp = 1; pp < b.length() - 1 - j - 1; pp++) {
                            if (b.charAt(pp) != b.charAt(j + 1 + pp)) {
                                oo = 1;
                                break;
                            }
                        }
                        if (oo == 0) {
                            gg = kk;
                        }

                    }

                }
                int p = gg;
                if (gg == b.length()) {
                    int tt = 0;

                    for (int ll = b.length() - 1 - j - 1, jj = 1; ll > 0; ll--, jj++) {
                        if (b.charAt(0) == b.charAt(j + 1 + ll)) {
                            tt = jj;
                        }
                    }
                    gg -= tt;
                }
                if (p == b.length()) {
                    bb = gg;
                } else {
                    bb = j + 1 - gg;
                }
            }

            i += bb;


        }

        System.out.println("没有找到");
    }

    public static void main(String[] args) {
        String a = "dffvff";
        String b = "dvf";
        System.out.println("下标从0开始的哦");
        bad(a, b);
        badd(a, b);
        //上面的坏字符查询，结果基本正确
        bad1(a, b); //在坏字符上，加上好后缀查询，结果基本也正确

        bad2(a, b); //操作正向的找坏字符
        bad3(a, b); //单纯的好后缀，只需要取出坏字符的代码即可，因为他们是没有必然关系的，只是用来判断而已
    }
}

至此，对应的BM算法操作完成，这里我们以最好的时间复杂度O（n/m）（虽然平均起来是O（n+m），当然是说明结合的，否则坏字符可以认为是n，好后缀，也可以是n，好后缀是认为，一般情况下，可能要多点次数）来进行表示，n是主串，m是模式串

应用：

BM算法比较高效，在实际开发中，特别是一些文本编辑器中，用于实现查找字符串功能（特别是不考虑哈希对比为O（1）的情况，那么相对来说是大大提高的）

Trie 树：

Trie 树，也叫"字典树"，它是一个树形结构，它是一种专门处理字符串匹配的数据结构，用来解决在一 组字符串集合中快速查找某个字符串的问题

比如：有 6 个字符串，它们分别是：how，hi，her，hello，so，see，我们可以将这六个字符串组成Trie树结构

Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起

其中，根节点不包含任何信息（即上面的表示目录"/"），每个节点表示一个字符串中的字符，从根节点到红色节点的一条路径表 示一个字符串（红色节点为叶子节点）

Trie树的插入：

Trie树的查找：

当我们在 Trie 树中查找一个字符串的时候，比如查找字符串"her"，那我们将要查找的字符串分割成单个的字符 h，e，r，然后从 Trie 树的根节点开始匹配，如图所示，蓝色的路径就是在 Trie 树中匹配的 路径

Trie 树是一个多叉树（即多路树或者多路查找树）：

虽然是多叉树，但是该叉树的变量基本没有上限，也就是说，单纯的利用链表变量是不行的，我们需要创建对应的类数组来保存其总变量

我们通过一个下标与字符依次映射的数组，来存储子节点的指针

假设我们的字符串中只有从 a 到 z 这 26 个小写字母，我们在数组中下标为 0 的位置，存储指向子节点a 的指针，下标为 1 的位置存储指向子节点 b 的指针，以此类推，下标为 25 的位置，存储的是指向的 子节点 z 的指针

如果某个字符的子节点不存在，我们就在对应的下标的位置存储 null

那么如果保存节点呢，一般是如下：

public class TrieNode {
    public char data; //保存对应的字符
    public TrieNode[] children = new TrieNode[26]; //该节点拥有的变量，由于最大只有26，所以我们只需要定义26个长度即可，他就可以认为是对应的子节点
    public boolean isEndingChar = false; //代表到这个节点是存在的意思
    public TrieNode(char data) {
        this.data = data;
   }
}

当我们在 Trie 树中查找字符串的时候，我们就可以通过字符的 ASCII 码减去"a"的 ASCII 码（即当前的保存的字符），迅速找到 匹配的子节点的指针，并使得满足上面数组的长度26

比如，d 的 ASCII 码减去 a 的 ASCII 码就是 3，那子节点 d 的指针就存储在数组 中下标为 3 的位置中

现在我们来进行编写，可以先看完后，自己编写一个：

package com.lagou;

/**
 *
 */
public class test55 {

    //首先就是对应的类
    public static class TrieNode {
        public char data; //保存对应的字符
        public TrieNode[] children = new TrieNode[26]; //该节点拥有的变量，由于最大只有26，所以我们只需要定义26个长度即可，他就可以认为是对应的子节点
        public boolean isEndingChar = false; //代表到这个节点是存在的意思

        public TrieNode(char data) {
            this.data = data;
        }
    }

    //定义起始节点
    public static TrieNode root = new TrieNode('/'); //默认无效字符

    //创建插入节点（字符串）
    public static void insert(String a) {
        //我们先定义临时变量得到起始节点，不让他改变指向
        TrieNode node = root;

        //现在我们来进行保存
        for (int i = 0; i < a.length(); i++) {
            //我们先得到开始的一个
            char c = a.charAt(i);
            //得到下标，由于是a-z的，那么我们减去97，来得到对应的数组下标
            int i1 = c - 97;
            //如果对应的下标是null，那么添加上去
            if (node.children[i1] == null) {
                node.children[i1] = new TrieNode(c);
            }
            node = node.children[i1];

        }
        //从上面的循环来看，他始终对后面进行添加，当退出时，我们需要为最后一个定义标识，使得保存的该位置是一个字符串
        node.isEndingChar = true;
        //因为，如果你不是该字符串，那么必然是不会是true的


    }

    //查找字符串（节点）
    public static void select(String a) {
        //我们先定义临时变量得到起始节点，不让他改变指向
        TrieNode node = root;

        //现在我们来进行查找
        for (int i = 0; i < a.length(); i++) {
            //我们先得到开始的一个
            char c = a.charAt(i);
            //得到下标，由于是a-z的，那么我们减去97，来得到对应的数组下标
            int i1 = c - 97;
            //如果对应的下标是null，那么说明没有，直接退出
            if (node.children[i1] == null) {
                System.out.println("没有该字符串");
                return;
            }
            node = node.children[i1];

        }
        if (node.isEndingChar == true) {
            //如果是true，说明是存在的
            System.out.println("有该字符串");

        } else {
            System.out.println("没有该字符串");
        }

    }

    public static void main(String[] args) {
        insert("hello");
        insert("her");
        insert("hi");
        insert("how");
        insert("see");
        insert("so");
        select("how");
    }

}

时间复杂度：

如果要在一组字符串中，频繁地查询某些字符串，用 Trie 树会非常高效，构建 Trie 树的过程，需要扫描所有的字符串，时间复杂度是 O（n）（n 表示所有要添加的字符串的长度和），但是一旦构建成功之后，后续的查询操作会非常高效，每次查询时，如果要查询的字符串长度是 k，那我们只需要比对大约 k 个节点， 就能完成查询操作，跟原本那组字符串的长度和个数没有任何关系，所以说，构建好 Trie 树后，在其中 查找字符串的时间复杂度是 O（k），k 表示要查找的字符串的长度，即不要考虑类似于主串的长度了

所以说，如果主串特别长，那么最好使用该Trie树，那么比之前的BM算法（以坏字符为例），要高效很多，否则还是使用坏字符，因为他是可以一次就能操作很多次的，而主串少，那么他可能只需要一次就能解决，比如主串是adfgsj，模式串是adfgsh，很明显，一次就能打印"没有找到"，而这里却需要先创建主串的数组，然后操作模式串，所以加起来是12次（不考虑主串的创建，也是6次），即，在主串非常少时，使用BM算法（因为他们的移动是看主串的），否则使用Trie树，实际上BM算法平均起来可以认为是哈希对比（默认哈希算法为1），那么他的结果就是n-m+1，即主串越大，次数多，但是实际上他也与模式串有关系，模式串越小，次数也越多（所以这里进行补充，即主串和模式串相对相同的长度使用BM），虽然Trie树需要先创建主串，然后操作模式串，总共加起来就是n+m的次数，但是主串只需要一次创建，也就是说，他可以被其他人利用，所以我们认为他是O（1）（一般可以被其他人利用的数据，我们统称为O（1）），所以这里的Trie树，就是O（m），m是模式串长度，那么相对来说Trie树比较稳定，虽然在上面的n-m+1中，m=n时的1次要快，但胜在稳定，所以无论是BM还是Trie都可以使用，如果需要有时候快点，那么使用BM（一般需要在主串和模式串相对相同的长度），如果想总体快点，那么使用Trie，即实际上不考虑主串的创建，我们最好使用Trie，因为大多数的时候Trie比BM算法要快（除了对应的极端情况，或者某些n与m相差m-1的情况，即m<=n<=2m-1的情况，一般n是大于等于m的，否则自然也是"没有找到"，直接跳过了，而Trie却还需要循环，所以实际上是0<=n<=2m-1，空字符就是0，即长度为0，自然也直接退出），当然如果考虑主串的创建的话，那么任何时候（情况）都是比BM算法要慢的

典型应用：

利用 Trie 树，实现搜索关键词的提示功能

我们假设关键词库由用户的热门搜索关键词组成，我们将这个词库构建成一个 Trie 树，既然有创建好了，那么Trie自然比BM算法总体要快（因为这里的主串和模式串相对不相同的长度，即基本没有上面说明的对应情况）

当用户输入其中某个单词的时候，把这个词作为一个前缀子串在 Trie 树中匹配，为了讲解方便，我们假设词库里只有

hello、her、hi、how、so、see 这 6 个关键词

当用户输入了字母 h 的时候，我们就把以 h 为前缀的hello、her、hi、how 展示在搜索提示框内

当用户继续键入字母 e 的时候，我们就把以 he 为前缀的hello、her 展示在搜索提示框内，这就是搜索关键词提示的最基本的算法原理

这里要注意，某些提示下，可能会分词，也就是说，he，可以分成he，h，e，所以he有时候也会出现4个（对这里来说），看如下图中绿色的即可：

所以虽然上面说的he是两个，但是若有分词的话，可能就是4个了

图：

图的概念

图（Graph），是一种复杂的非线性表结构，之所以是复杂的，是因为一个节点可以有不同的子节点，所以与单纯的二叉树之类的数据结构是不同的，因为他们的节点个数基本固定，所以说是复杂的

图中的元素我们就叫做顶点（vertex）

图中的一个顶点可以与任意其他顶点建立连接关系

我们把这种建立的关系叫做边（edge），跟顶点相连接的边的条数叫做度（degree）

图这种结构有很广泛的应用，比如社交网络，电子地图，多对多的关系就可以用图来表示

边有方向的图叫做有向图，比如A点到B点的直线距离，微信的添加好友是双向的

边无方向的图叫无向图，比如网络拓扑图

带权图（weighted graph），在带权图中，每条边都有一个权重（weight），我们可以通过这个权重来表示 一些可度量的值

图的存储：

图最直观的一种存储方法就是，邻接矩阵（Adjacency Matrix）

邻接矩阵的底层是一个二维数组

无向图：如果顶点 i 与顶点 j 之间有边，我们就将 A[ i ] [ j ]和 A[ j ] [ i ]标记为 1

有向图：

如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，那我们就将 A[i] [j]标记为 1

同理，如果有一条箭头从顶点 j 指向顶点 i 的边，我们就将 A[j] [i]标记为 1

当然，上面的2和3是双向的（双向的权重可以不同），但各有对应的值，实际上有值也可以称为指向谁（有值才有指向的，比如1指向2，那么1中包含2这个值（二维数组）

当然，虽然是双向的，但是又何尝不是3对2的单向以及2对3的单向呢，实际上我们可以说，无向图，都是双向的

带权图：

数组中就存储相应的权重

很明显，之前的默认都是1（0代表没有边，或者就没有权的变量（针对类来说）），而带权图可以提高上限，一般权高的代表这条路优先操作，虽然这里只是给出说明而已，这里没有具体操作

我们通过上面的说明（基本是邻接矩阵），来写一个小操作，可以先看一遍，然后自己手动编写：

package com.lagou;

import java.util.ArrayList;
import java.util.List;

/**
 *
 */
public class test66 {
    //要操作直观的图，首先，我们先需要对应的变量，这里以二维数组内容进行说明（因为无论是有向图，还是无向图，还是带权图，都是二维数组的内容）

    //我们要保存对应的节点，自然需要类，而要保存很多节点，那么一般使用集合
    public List list;
    //由于该节点没有上下级关系（如没有二叉树的子节点和父节点的关系），所以该集合只是保存节点而已

    //节点保存好了，那么节点的信息是什么，我们知道，节点产生的信息，自然是需要其"边"的信息，以及"顶点"信息
    //由于二维数组是都包含好了，所以实际上节点里面没有信息，且他本身就是对应的顶点信息
    //所以，实际上节点没有信息，即节点只是用来确定"边"信息的

    //我们知道，边的关系以二维数组来表示，代表有指向那个边（边节点），以及总度（边的指向数，即边的条数）数

    //所以定义一个二维数组来保存边的关系
    int[][] i; //他的长度，由我们自己来操作
    //定义总边数（即总度，即所有的度的数量，而不是一个节点度的数量）
    int du;


    //从上面可以看出，我们的节点可以是Object，这里我们以String为主，看最后的操作代码就知道了
    //当然，由于节点信息和其边的信息都在当前类里面，所以我们需要进行初始化
    public test66(int n) {
        //这里传递参数：二维数组的长度，自然也是链表节点长度，那么就是如下：
        i = new int[n][n]; //因为对应图的二维数组是行和列是一样的，所以直接初始化即可
        //刚刚加上的节点，那么对应的总边数（所有节点，如果是该节点，那么我会说成，该节点的总边数，或者该节点的度，而不是总边数或者总度），自然是0
        du = 0;
        //在对应的链表中进行加上，来保存
        list = new ArrayList<>(n);

        //至此，对应节点链表以及二维数组操作完成


    }

    //现在，我们定义插入节点
    public void insertNode(Object node) {
        list.add(node);
        //后面没有什么操作，那么很明显，实际上节点的数量是可以凭空产生的，即节点与边的关系只是逻辑上的关系而已，所以并不是有节点就一定要连接边
    }

    //插入节点后，自然就是插入边
    public void insertEdge(int a, int b, int c) {
        //我们知道，边是在二维数组里面的，所以说，插入的边就是给二维数组赋值，只是逻辑上记得要与节点对应
        i[a][b] = c;
        //插入一个边，那么总度数，自然要加1
        du++;
    }

    //定义返回权值，即二维数组对应的值
    public int getWeight(int a, int b) {
        return i[a][b];
    }

    //返回节点的数据，我们知道节点本身就是顶点，那么他的数据就是保存的节点信息
    public Object getNode(int i) {
        //给出参数，是为了要查看哪（也可以说成"那"，但通常是手滑打出的字）个节点
        return list.get(i);
    }

    //得到边的总数量
    public int getEage() {
        return du;
    }

    //得到节点的总数量
    public int getNodeAll() {
        return list.size();
    }

    //至此，边和节点的插入，以及节点边的总数量，以及对应边的权值以及对应节点的数据，这6个基本操作编写完成
    //现在我们来进行测试
    public static void main(String[] args) {
        //为了更好的测试，我们操作初始化的信息少点

        //对应节点和边的数量
        int a = 4;
        //当然，上面定义的是最大值，所以要注意

        //定义节点的信息，这里就在前面说明了以String的信息为主，所以这里就是如下：
        String[] s = {"v1", "v2", "v3", "v4"};
        //创建对象
        test66 t = new test66(a);
        //插入节点
        for (String c : s) {
            t.insertNode(c);
        }

        //现在我们进行插入边
        t.insertEdge(0, 1, 2);
        //t.insertEdge(0, 1, 2);，因为是逻辑的，所以如果这里也加上的话，会使得对应的总边数加1
        //t.insertEdge(1, 1, 2);，这个也会，但实际上却不能操作，因为没有自身指向自身的，可是这里的总边数还是会加1，所以说他是逻辑的
        t.insertEdge(0, 2, 5);
        t.insertEdge(2, 3, 8);
        t.insertEdge(3, 0, 7);
        /*
        这里我要说明一下，二维数组的表示图形显示：
        你可以这样（第一种）
        v1 v2 v3 v4
     v1 0  2  5  0
     v2 0  0  0  0
     v3 0  0  0  8
     v4 7  0  0  0
        很明显，每一行代表二维数组中的i[a]，而不是i[a][b]的[b]
        你也可以这样（第二种）
        v1 v2 v3 v4
     v1 0  0  0  0
     v2 2  0  0  0
     v3 5  0  0  7
     v4 0  0  8  0
         很明显，每一列代表二维数组中的i[a]，而不是i[a][b]的[b]
         这都是不同的表示形式，至于使用那一种，看你自己，因为他们都可以
         只是一般情况下，第一种好点，因为行看起来比较整齐，且我们通常喜欢看行，然后是列，当然主要看自己的习惯
         */
        //这里以第一种为主
        //我们来观察他的信息，v1这个节点，他指向了v2和v3（逻辑上的），v3指向v4，v4指向v1，对应的值就是权值
        //至此，该基本图操作完毕
        
        System.out.println("结点个数是：" + t.getNodeAll());
        System.out.println("边的个数是：" + t.getEage());
    }
}

当然，上面我们可以看到，他只是给出逻辑上的指向，所以只要该二维数组的值是对应的图即可，即手动的设置是否是有向图，还是无向图，还是带权图（这里一般结合前面的，使得不默认为1），所以这里看你如何的添加了（这里就是有向图），当然，这里并没有给出什么限制条件，因为我们只操作主要的，你可以自己进行操作限制，或者修改某些细节，比如添加相同的边，总边数也会增加，我们只需要设置判断是否有权值即可，没有权值，那么增加总边数，否则使得总边数不增加，并覆盖对应的权值（修改成自身的再次的设置的权重）等等，这样的思路也是可以的

邻接表：

用邻接矩阵来表示一个图，虽然简单、直观，但是比较浪费存储空间

特别是对于无向图来说，如果 A[i] [j]等于 1，那 A[j] [i]也肯定等于 1

而对于他（无向图），实际上，我们只需要存储一个就可以了，也就是说，无向图的二维数组中，如果我们将其用对角线划分为上下两部分，那我们只需要利用上面或者下面这样一半的空间就足够了，另外一半白白浪费掉了 （使得节省空间）

还有，如果我们存储的是稀疏图（Sparse Matrix），也就是说，顶点很多，但每个顶点的边并不多， 那邻接矩阵的存储方法就更加浪费空间了（因为对应的值都是默认值，并没有使用到，在前面的例子中，可以发现，有很多个都是0），比如微信有好几亿的用户，对应到图上就是好几亿的顶点，但是每个用户的好友并不会很多，一般也就三五百个而已，如果我们用邻接矩阵来存储，那绝大部分的存储空间都被浪费了（因为没有使用，加上行是100，列是100，但是其中一行只有一个空间利用了，那么其他的空间自然是浪费的），所以总体而言，无论是无向图还是有向图，在边少的情况下，会浪费空间（虽然无向图，可以节省一半），其中带权图，只是使得权能够突破1而已，所以他是附加在无向图或者有向图的，所以不要理会

针对上面邻接矩阵比较浪费内存空间的问题，我们来看另外一种图的存储方法，邻接表（Adjacency List）

每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点

图中画的是一个有向图的邻接表存储方式，每个顶点对应的链表里面，存储的是指向的顶点

在前面的二维数组中，存储的是对于的指向的权重，而集合存储的是所有的顶点，并且该顶点保存的是其本身的值，现在我们将每一个顶点看成一个类，然后该类是一个链表节点，后面连接的块（节点），代表前面顶点所指向的顶点，里面也包括了该路线的权值

如果该点还指向其他顶点，则继续在块后面添加，例如A指向了B，权值是4，那么A后面就加上一块，之后发现A还指向D权值是5，那么就在块尾继续添加一块，其实也就是数组+链表的结构，但是好像他也只是一个指向而已，并不是多条线路，所以从上到下的添加边时，若先添加的是D，那么在后面的打印中，可能是D先出现，你交换位置就知道了（在后面会说明），即他们是一个一个的打印的，而不会将其指向的顶点的指向的顶点进行打印（因为只打印边），即只操作第一级别，当然，这是因为其他的顶点由其他数组下标的值来进行保存的，所以这里是分开的保存，当然，二维数组基本也是，但是总体结合起来就是图了

根据邻接表的结构和图，我们不难发现，图其实是由顶点和边组成的，所以我们就抽象出两种类，一个 是Vertex顶点类，一个是Edge边类，注意：这里是将开始的节点称为顶点，顶点指向的顶点称为边类（这里要注意，之所以是边类，在程序里面会说明）

具体代码如下，可以先看一遍，然后自己编写：

package com.lagou;

import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;

/**
 *
 */
public class test77 {

    //定义顶点类
    public class Vertex {
        String name; //顶点名称，也就是之前的顶点的值，只是这里是节点了，我们保存该名称即可
        Edge next;

        public Vertex(String name, Edge next) {
            this.name = name;
            this.next = next;
        }

    }

    //定义边类（也就是指向的顶点），这里之所以看成是边类，是因为，好像这里的内容就是边的信息，所以我们一般也会将该类称为边，内容称为指向顶点的内容（包含顶点）
    public class Edge {
        String name; //被指向的顶点，或者说，就是顶点，所以可以认为这里定义的是边的信息
        int weight; //对应的权重（权，权值）
        Edge next; //指向的下一个边

        public Edge(String name, int weight, Edge next) {
            this.name = name;
            this.weight = weight;
            this.next = next;
        }
//之所以这样，是因为数组有很多顶点，那么其链表只需要保存边即可，所以因为数组保存顶点，链表保存边，即我们也会称为分开的保存

    }

    //类已经定义好了，那么我们来进行操作，即上面我们定义了顶点，以及边（指向了顶点），即他们的类信息
    //在前面我们操作时，是以集合保存顶点的，现在，为了不操作二维数组，所以我们来进行直接使用链表，当然，之前的集合本质上也是数组，所以这里本质上就是数组加链表
    //我们先定义数组，当然，该数组我们可以使用集合，这里考虑使用map集合的数组
    Map<String, Vertex> map; //前面的String也用来保存顶点名称的，这样，就不用我们来考虑下标来得到名称了，使得可以对应，这就是使用map集合的原因
    
    //这里就不考虑对应的顶点总边了（当然，考虑所有顶点总边也行），因为我们选择主要的操作来进行操作的（前面在说明过了，即在BM算法代码中有说明"我们只会选择主要的情况来操作"）

    //我们进行初始化
    public test77() {
        map = new HashMap<>();
    }

    //首先我们需要进行两个主要操作，即添加顶点以及添加边（包含顶点）

    //添加顶点
    public void insertNode(String a) {
        //参数自然就是顶点的名称
        Vertex aa = new Vertex(a, null); //一开始是没有边的
        map.put(a, aa);

    }

    //添加边，我们需要参数如下：被指向顶点的名称，权值，给哪个对应的顶点
    public void insertEdge(String a, String b, int c) {
        //其中a代表以及添加的顶点名称，b代表被指向的顶点名称，c代表权值
        //那么这里为了先考虑若没有对应的顶点怎么办，所以我们操作补偿

        Vertex vertex = map.get(a);
        if (vertex == null) {
            vertex = new Vertex(a, null); //一开始是没有边的
            map.put(a, vertex); //之所以这样，是为了后面可以再次的得到（因为指向改变了）
        }
        //如果没有顶点，自然我们手动的创建

        //现在我们来添加边

        if (vertex.next == null) {
            vertex.next = new Edge(b, c, null);
        } else {
            Edge temp = vertex.next;
            while (true) {

                if (temp.next == null) {
                    //到这里代表没有边，那么添加
                    temp.next = new Edge(b, c, null);
                    return;
                }
                temp = temp.next;
            }
        }

    }

    //上面我们编写完毕，但为了更好的操作遍历，我们可以写一个遍历方法
    public void Select() {
        //我们知道他是map集合，他的总体打印一般需要先进行转换（是他的操作，而不是我之前手写的map集合，因为我有对应的方法）
        Set<Map.Entry<String, Vertex>> entries = map.entrySet();
        Iterator<Map.Entry<String, Vertex>> iterator = entries.iterator();
        while (iterator.hasNext()) {
            Map.Entry<String, Vertex> entry = iterator.next();
            Vertex vertex = entry.getValue(); //得到其中数组的顶点
            Edge edge = vertex.next; //得到该顶点的下一个边类
            while (edge != null) {
                System.out.println(vertex.name + " 指向 " + edge.name + " 权值为：" + edge.weight);
                edge = edge.next;
            }

        }
    }

    public static void main(String[] args) {
        test77 graph = new test77();
        graph.insertNode("A");
        graph.insertNode("B");
        graph.insertNode("C");
        graph.insertNode("D");
        graph.insertNode("E");
        graph.insertNode("F");
        //给c这个顶点，添加A这个顶点，对应的权值是1，后面依次类推即可
        graph.insertEdge("C", "A", 1);
        graph.insertEdge("F", "C", 2);
        graph.insertEdge("A", "B", 4);
        graph.insertEdge("E", "B", 2);
        graph.insertEdge("A", "D", 5); //可以与graph.insertEdge("A", "B", 4);交换位置，可以发现打印顺序从原来的先输出B，变成了先输出D
        graph.insertEdge("D", "F", 4);
        graph.insertEdge("D", "E", 3);
        graph.Select();

    }
    //当然，上面的添加也是逻辑性的，虽然他们可以任意的添加，但我们可以发现，边的添加可以是相同的，这是不好的情况，而顶点，因为map集合的原因，相同的则会覆盖（会使得没有边，因为方法的缘故），当然，这些问题是细节问题，这里没有理会，你可以选择进行操作修改
    //这里实际上也与二维数组一样的，都是逻辑上的连接
    
    //因为实际上图就是逻辑结构
}

所以通过上面的代码，我们才会说，图是顶点和边来操作的，因为边的指向包含了指向的顶点，并且，这样可以保证数据是一致的

我们也可以发现，实际上被指向的顶点和边是一起的（在一个类里面，并且总体被一个顶点指向）

至此通过前面的说明以及代码的实现，所以我们可以说，这里的数组加链表完全的利用了空间

时间复杂度：

邻接表：访问所有顶点的时间为 O（V）（一个数组），而查找所有顶点的邻居一共需要 O（E）（连接的邻居，自然不会也是数组，所以不会是相乘） 的时间，所以总的时间复杂度是O（V + E），V是顶点数，E是边数（该边数通常比V大，在极端情况下，要比V少一个，比如就一条线）

邻接矩阵：

查找每个顶点的邻居需要 O（V）（二维数组） 的时间，所以查找整个矩阵的时候需要 O（V^2） 的时间，V是顶点数（这里找边数，却要找顶点数，所以是V^2）

图的遍历 ：

遍历是指从某个节点出发，按照一定的的搜索路线，依次访问对数据结构中的全部节点，且每个节点仅访问一次

当然，前面的代码中，因为先后顺序，所以A顶点信息会先打印出来

前面已经讲过了二叉树的节点遍历（比如广度优先和深度优先（也分为前序，中序，后序））

类似的，图的遍历是指，从给定图中任意指定的顶点（称为初始点）出发，按照某种搜索方法沿着图的边访问图中的所有顶点，使每个顶点仅被访问一次，这个过程称为图的遍历，遍历过程中得到的顶点序列称为图遍历序列，当前，上面代码中，不是这样的遍历，他只是打印出对应的指向终点而而已

图的遍历过程中，根据搜索方法的不同，又可以划分为两种搜索策略：

深度优先搜索以及广度优先搜索

深度优先搜索（DFS，Depth First Search） ：

深度优先搜索，从起点出发，从规定的方向中选择其中一个不断地向前走，直到无法继续为止，然后尝试另外一种方向，直到最后走到终点，就像走迷宫一样，尽量往深处走，这里我们就不会只操作第一级别了，即不会像前面的代码一样，只保证顶点指向的顶点（他操作了分开的保存）

DFS 解决的是连通性的问题，即，给定两个点，一个是起始点，一个是终点，判断是不是有一条路径能从起点连接到终点，起点和终点，也可以指的是某种起始状态和最终的状态，问题的要求并不在乎路径 是长还是短，只在乎有还是没有，所以这里要进行注意

假设我们有这么一个图，里面有A、B、C、D、E、F、G、H，8 个顶点，点和点之间的联系如下图所示， 对这个图进行深度优先的遍历

基本通常依赖栈（Stack），因为其特点是满足这里的后进先出（LIFO）的

第一步，选择一个起始顶点（先不给出终点，这里先来看看他的流程是什么），例如从顶点 A 开始，把 A 压入栈，标记它为访问过（用红色或者黄色标记），并输出到结果中

第二步，寻找与 A 相连并且还没有被访问过的顶点，顶点 A 与 B、D、G 相连，而且它们都还没有被访 问过，我们按照字母顺序处理，所以将 B 压入栈，标记它为访问过，并输出到结果中

第三步，现在我们在顶点 B 上，重复上面的操作，由于 B 与 A、E、F 相连，如果按照字母顺序处理的 话，A 应该是要被访问的，但是 A 已经被访问了，所以我们访问顶点 E，将 E 压入栈，标记它为访问过，并输出到结果中

第四步，从 E 开始，E 与 B、G 相连，但是B刚刚被访问过了，所以下一个被访问的将是G，把G压入 栈，标记它为访问过，并输出到结果中

第五步，现在我们在顶点 G 的位置，由于与 G 相连的顶点都被访问过了，类似于我们走到了一个死胡同，必须尝试其他的路口了

所以我们这里要做的就是简单地将 G 从栈里弹出，表示我们从 G 这里已 经无法继续走下去了，看看能不能从前一个路口找到出路

也就是说，如果发现周围的顶点都被访问了，就把当前的顶点弹出

第六步，现在栈的顶部记录的是顶点 E，我们来看看与 E 相连的顶点中有没有还没被访问到的，发现它们都被访问了（虽然在栈中被弹出，但是访问的标记他还是在的，只是在栈里面没有而已，但是其他已经保存的还是在的），所以把 E 也弹出去

第七步，当前栈的顶点是 B，看看它周围有没有还没被访问的顶点，有，是顶点 F，于是把 F 压入栈， 标记它为访问过，并输出到结果中（下面的F是我加上的，使得图片变的合理）

第八步，当前顶点是 F，与 F 相连并且还未被访问到的点是 C 和 D，按照字母顺序来，下一个被访问的 点是 C，将 C 压入栈，标记为访问过，输出到结果中

第九步，当前顶点为 C，与 C 相连并尚未被访问到的顶点是 H，将 H 压入栈，标记为访问过，输出到结 果中

第十步，当前顶点是 H，由于和它相连的点都被访问过了，将它弹出栈

第十一步，当前顶点是 C，与 C 相连的点都被访问过了，将 C 弹出栈

第十二步，当前顶点是 F，与 F 相连的并且尚未访问的点是 D，将 D 压入栈，输出到结果中，并标记为 访问过

第十三步，当前顶点是 D，与它相连的点都被访问过了，将它弹出栈，以此类推，顶点 F，B，A 的邻居 都被访问过了，将它们依次弹出栈就好了，最后，当栈里已经没有顶点需要处理了，我们的整个遍历结束

即结果就是：A，B，E，G，F，C，H，D

广度优先搜索（BFS，Breadth First Search） ：

直观地讲，它其实就是一种"地毯式"层层推进的搜索策略，即先查找离起始顶点最近的，然后是次近 的，依次往外搜索

假设我们有这么一个图，里面有A、B、C、D、E、F、G、H，8 个顶点，点和点之间的联系如下图所示， 对这个图进行深度优先的遍历

依赖队列（Queue），先进先出（FIFO）

一层一层地把与某个点相连的点放入队列中，处理节点的时候正好按照它们进入队列的顺序进行

第一步，选择一个起始顶点（先不给出终点，这里先来看看他的流程是什么），让我们从顶点 A 开始，把 A 压入队列，标记它为访问过（用红色或者黄色标记）

第二步，从队列的头取出顶点 A，打印输出到结果中，同时将与它相连的尚未被访问过的点按照字母大小顺序压入队列，同时把它们都标记为访问过，防止它们被重复地添加到队列中

第三步，从队列的头取出顶点 B，打印输出它，同时将与它相连的尚未被访问过的点（也就是 E 和 F） 压入队列，同时把它们都标记为访问过

第四步，继续从队列的头取出顶点 D，打印输出它，此时我们发现，与 D 相连的顶点 A 和 F 都被标记 访问过了，所以就不要把它们压入队列里

第五步，接下来，队列的头是顶点 G，打印输出它，同样的，G 周围的点都被标记访问过了，我们不做 任何处理

第六步，队列的头是 E，打印输出它，它周围的点也都被标记为访问过了，我们不做任何处理

第七步，接下来轮到顶点 F，打印输出它，将 C 压入队列，并标记 C 为访问过

第八步，将 C 从队列中移出，打印输出它，与它相连的 H 还没被访问到，将 H 压入队列，将它标记为 访问过

第九步，队列里只剩下 H 了，将它移出，打印输出它，发现它的邻居都被访问过了，不做任何事情

第十步，队列为空，表示所有的点都被处理完毕了，程序结束

至此，我们可以发现：

广度优先搜索结果就是：A，B，D，G，E，F，C，H，感觉是总中间往外扩散，所以是广度

深度优先搜索结果就是：A，B，E，G，F，C，H，D，感觉一路找过去，所以是深度

当然他们都是无向图，这里要注意

最短路径问题：

广度优先搜索，一般用来解决最短路径的问题

因为我们知道，前面的操作是无向的，所以可以操作直接的标记，但是在有向的情况下，A只能操作D和G，又因为深度，他只会操作一路找过去，所以并不能确定当前的路径是否是最短的，或者说，很难确定，但是广度，由于是扩散的，所以很容易的知道哪个路径先到终点，那么谁就是最短路径

从上面的图中，可以得出（没有指向的不会操作，之前的都是无向图）：

深度优先遍历（搜索）是：A，D，F，C，H，G，E，B

广度优先遍历（搜索）是：A，D，G，F，E，C，B，H

这里，我们就选择，有向图来进行编写代码（作为主要的情况来操作）：

我们先编写基础的代码，然后来选择说明深度和广度谁能操作最短路径

可以先看完后，在自行进行编写（以上面的图为例的添加节点）：

package com.lagou;

import java.util.*;

/**
 *
 */
public class test88 {
    //这里以有向图来进行操作，顺便也结合带权（带权图）
    //我们这里还是使用链表加数组来表示，所以有些代码利用之前的
    public class Vertex {
        String name;
        Edge next;
        boolean b = false; //默认没有访问，注意：边不需要进行设置该变量，因为其不是唯一，这里代表唯一的，边只是定义其指向信息的，而不能是顶点

        //所以这里更加的说明一下，边就是边，而不是顶点
        public Vertex(String name, Edge next) {
            this.name = name;
            this.next = next;
        }

    }

    public class Edge {
        String name;
        int weight;
        Edge next;


        public Edge(String name, int weight, Edge next) {
            this.name = name;
            this.weight = weight;
            this.next = next;
        }


    }

    //注意：因为他们是不同的类，我存放在栈里面，一般直接存放其名称即可，因为我们可以通过名称来得到其节点（虽然他们是分开的）
    //当然，你可能会问，设置相同的类不就好了，实际上也行，只是总不能所有的类都有权重（权值吧），因为一开始是没有边的，你可以再编写测试后，将Edge类删除，然后在Vertex类里加上权重变量，可以发现，虽然添加节点，需要添加权重，其他的代码只需要改变将Edge变成Vertex即可，结果还是一样的，因为其操作的内容还是一样，只是连接的是当前类而已，但是一开始怎么能够有权重呢
    //所以如果你不操作权重，那么可以是相同的类（虽然就算操作了也行），因为我们只要指向就行，这里为了完美操作，我们就加上权重了，并且定义两个类，来具体区分，总不能又当顶点，也当边吧，要明确的分工，虽然需要多定义一个类

    Map<String, Vertex> map;

    public test88() {
        map = new HashMap<>();
    }

    public void insertNode(String a) {

        //这里我们进行修改
        if (map.get(a) == null) {
            Vertex aa = new Vertex(a, null);
            map.put(a, aa);
        }
        //总不能使得操作覆盖，使得没有边了吧

    }

    public void insertEdge(String a, String b, int c) {

        Vertex vertex = map.get(a);
        if (vertex == null) {
            vertex = new Vertex(a, null);
            map.put(a, vertex);
        }


        if (vertex.next == null) {
            vertex.next = new Edge(b, c, null);
        } else {
            Edge temp = vertex.next;
            Edge temp2 = vertex.next;
            while (true) {
                //为了后续队列的操作，这里需要进行大小的判断，由于不用考虑头，所以代码相对简单

                //防止添加相同的边
                if (temp.name == b) {
                    temp.weight = c;
                    return;
                }

                if (temp.name.hashCode() > b.hashCode()) { //那么就说明新添加的比较小，所以对应的要放在前面
                    if (temp2 != vertex.next) {
                        //进入这里，说明他已经经历了一个循环
                        Edge j = new Edge(b, c, null);
                        temp2.next = j;
                        j.next = temp;
                    } else {
                        //进入这里，说明就是第一次
                        Edge j = new Edge(b, c, null);
                        vertex.next = j;
                        j.next = temp2;
                    }
                    return;
                }

                if (temp.next == null) {
                    temp.next = new Edge(b, c, null);
                    return;
                }
                //其他情况就是大的，当然，这里可以不用判断，因为外面就是大的了，虽然也可以判断，之前的链表操作就是判断的，这里就不判断了，反正是一样的
                temp2 = temp;
                temp = temp.next;
            }
        }

    }

    public void Select() {

        Set<Map.Entry<String, Vertex>> entries = map.entrySet();
        Iterator<Map.Entry<String, Vertex>> iterator = entries.iterator();
        while (iterator.hasNext()) {
            Map.Entry<String, Vertex> entry = iterator.next();
            Vertex vertex = entry.getValue();
            Edge edge = vertex.next;
            while (edge != null) {
                System.out.println(vertex.name + " 指向 " + edge.name + " 权值为：" + edge.weight);
                edge = edge.next;
            }

        }
    }

    //当然，对应的有向图是逻辑的，所以主要看对应的添加信息的方式（后面的添加是有向图的），所以这里我们直接的编写广度优先搜索和深度优先搜索即可

    //深度优先搜索
    public void Select1(String a) {
        //要完成深度优先搜索，我们可以先选择看之前的图片，也就是"针对上面邻接矩阵比较浪费内存空间的问题，我们来看另外一种图的存储方法，邻接表（Adjacency List）"这段话下面的图片
        //我们操作的就是他，所以我们添加的是有向图
        //那么由于我们需要一个起点，所以这个参数a就是起点的节点名称，当然，后面会给出一个终点的操作
        //我们既然选择该起点，那么就需要将他进行标记，前提，首先需要都进行解除，因为，当多次的执行，那么标记总不能重复使用吧

        //初始化标记
        Set<String> strings = map.keySet();
        Iterator<String> iterator = strings.iterator();
        while (iterator.hasNext()) {
            String next = iterator.next();
            map.get(next).b = false;
        }
        //初始化完成后，现在，我们进行深度遍历
        //定义输出的数组信息
        String[] array = new String[map.size()];
        //定义起始下标
        int i = 0;
        //首先得到该节点
        Vertex vertex = map.get(a);
        //然后输出信息（放在数组里面）
        array[i] = vertex.name;
        i++;

        //定义一个栈
        Stack<Object> stack = new Stack<>();
        stack.push(vertex.name); //入栈
        vertex.b = true; //设置标记
        //然后看看该节点对应的边的内容节点最先是谁，由于对应都是由字母进行设置的，所以实际上可以使用他们本身的哈希值来决定先后

        while (true) {
            //定义最先内容
            String na = null;
            Edge edge = vertex.next;
            if (edge != null) {

                //只有，有下一个的，才会操作这里的操作
                while (edge != null) {
                    //因为添加的原因，所以其链表第一个或者前一个就是最小的
                    if (map.get(edge.name).b == false) {
                        na = edge.name;
                        //找到最小就不用在循环了
                        break;
                    }
                    edge = edge.next;
                }

                //若代表有值则为true，否则都是标记的，那么也直接的出栈
                if (na != null) {
                    //上面得到了最先的顺序，那么我们加入栈
                    stack.push(na);

                    array[i] = na;
                    i++;
                    map.get(na).b = true; //设置标记

                } else {
                    //都标记了，那么直接的出栈
                    stack.pop();
                }

            } else {
                //没有下一个了，那么直接的出栈
                stack.pop();
            }

            //如果没有栈内容了，那么说明都出栈了，即都遍历完毕了
            if (stack.isEmpty()) {
                break;

            }
            //获得当前顶点
            String peek = (String) stack.peek();
            //改变顶点
            vertex = map.get(peek);


        }

        //打印遍历的信息
        System.out.print("[");
        for (int ii = 0; ii < array.length; ii++) {
            if (ii == array.length - 1) {
                System.out.print(array[ii]);
            } else {
                System.out.print(array[ii] + ",");
            }
        }
        System.out.println("]");

    }

    //至此，深度优先搜索操作完毕

    //现在我们来编写广度优先搜索
    public void Select2(String a) {
        //前面几乎与深度优先搜索一样
        Set<String> strings = map.keySet();
        Iterator<String> iterator = strings.iterator();
        while (iterator.hasNext()) {
            String next = iterator.next();
            map.get(next).b = false;
        }
        //初始化完成后，现在，我们进行广度遍历
        //定义输出的数组信息
        String[] array = new String[map.size()];
        //定义起始下标
        int i = 0;
        //首先得到该节点
        Vertex vertex = map.get(a);

        //定义一个队列
        Queue<String> queue = new LinkedList<>();
        queue.offer(vertex.name); //入队
        vertex.b = true; //设置标记
        //出队
        String poll = queue.poll();
        array[i] = poll;
        i++;

        while (true) {
            //操作入队
            Edge edge = vertex.next;
            if (edge != null) {

                while (edge != null) {
                    //这里我们需要有顺序的进行入队，所以我们需要将链表进行排列，当然，这个操作，我们需要在添加边中进行
                    //前面的添加操作中有说明了，他是小的在前面，大的在后面，所以这里直接的入队即可

                    if (map.get(edge.name).b == false) {
                        queue.offer(edge.name);
                        map.get(edge.name).b = true; //标记
                    }
                    edge = edge.next;
                }


            }
            //最后一个出队也到这里，说明操作完毕
            if (queue.isEmpty()) {
                break;

            }
            //上面将相关的都入队后，然后外面操作出队，若没有入队的，那么自然是对应下一个出队
            String poll1 = queue.poll();

            array[i] = poll1;
            i++;

            vertex = map.get(poll1); //得到出队的顶点
            edge = vertex.next; //操作出队顶点的入队


        }
        //打印遍历的信息
        System.out.print("[");
        for (int ii = 0; ii < array.length; ii++) {
            if (ii == array.length - 1) {
                System.out.print(array[ii]);
            } else {
                System.out.print(array[ii] + ",");
            }
        }
        System.out.println("]");


    }
    //至此，广度优先遍历操作完毕

    public static void main(String[] args) {
        test88 graph = new test88();
        graph.insertNode("A");
        graph.insertNode("B");
        graph.insertNode("C");
        graph.insertNode("D");
        graph.insertNode("E");
        graph.insertNode("F");


        //给c这个顶点，添加A这个顶点，对应的权值是1，后面依次类推即可
        graph.insertEdge("C", "A", 1);
        graph.insertEdge("F", "C", 2);
        graph.insertEdge("A", "D", 5);
        graph.insertEdge("A", "B", 4);
        graph.insertEdge("E", "B", 2);
        graph.insertEdge("D", "F", 4);
        graph.insertEdge("D", "E", 3);


        graph.Select();

        graph.Select1("A"); //[A,B,D,E,F,C]
        graph.Select2("A"); //[A,B,D,E,F,C]

        test88 aa = new test88();
        aa.insertNode("A");
        aa.insertNode("B");
        aa.insertNode("C");
        aa.insertNode("D");
        aa.insertNode("E");
        aa.insertNode("F");
        aa.insertNode("G");
        aa.insertNode("H");
        aa.insertEdge("A", "D", 3);
        aa.insertEdge("A", "G", 3);
        aa.insertEdge("B", "A", 3);
        aa.insertEdge("B", "F", 3);
        aa.insertEdge("C", "H", 3);
        aa.insertEdge("D", "F", 3);
        aa.insertEdge("E", "B", 3);
        aa.insertEdge("F", "C", 3);
        aa.insertEdge("G", "E", 3);
        aa.Select();

        aa.Select1("A"); //[A,D,F,C,H,G,E,B]
        aa.Select2("A"); //[A,D,G,F,E,C,B,H]

    }

}

我们也操作了该有向图：

那么对应的遍历如下：

深度优先遍历（搜索）：A，B，D，E，F，C

广度优先遍历（搜索）：A，B，D，E，F，C

我们可以发现，他们是一样的，所以在某些时候，他们是可以一样的，所以这里注意即可

继续回到前面的问题，如何得出最短路径，我们知道，深度优先搜索，他是一路找的，从代码里面可以看出，他先选择一个路，直到找不到了才会返回，如果我们使用深度来操作最短，那么我们基本是得不到具体路径的，因为有标志（且由于是按照字母顺序来的，所以如果上面的B指向E，E指向F，那么以A为起点，F为终点，我们只能得到ABEDF，然后因为标志，所以下一次不可能指向或者获得E了，但是实际上最短路径是ADF，即是错误的最短路径，所以我们不会考虑深度），所以深度是基本操作不了最短的，而广度可以，因为他是分散的，只要谁先找到E，那么对应的路径就是最短的，具体代码如下（以上面这个图片为例子）：

package com.lagou;

import java.util.*;

/**
 *
 */
public class test99 {

    //这里要考虑一个问题，如果广度操作最短路径那么需要某些自定义的变量吗，我稍微思考了一下：
    //实际上单纯的循环就能解决，比如我指定起点A，终点E，那么我们循环A的所有节点，然后对其节点对应的顶点也进行循环，自然也能找到终点E
    //所以我们唯一要做的，就是如何保存路径，我们也知道他的最短路径是ADE，可以怎么保存呢，因为我们第一次扩散，是BE，他的对应A节点可以保存，但是若到第二个扩散D开始时，虽然找到E，但是你总不能格外定义一个变量保存他的A吧
    //就算你能，那么第三次扩散，第n次扩散，你怎么保存，所以只要解决保存的问题，那么该最短路径就解决了
    //我思考良久，我决定加上一个变量，我对每个边（Edge）中加上头节点变量

    public class Vertex {
        String name;
        Edge next;
        Vertex prev; //用来保存头节点，只要每个节点都进行保存，那么就能够得出路径，但是有个问题，该变量在添加边时，需要将指向的节点的该变量进行设置吗，答：不要，因为添加的节点中，因为一个节点是可以被多个节点指向的，所以不会让他进行初始化头
        //我们这个变量只是为了给广度进行操作，因为标志的原因，所以其他节点是就不能再次的指向他了，所以只在对应的广度里进行操作
        //注意：这里是给节点，而不是边，因为边只有对应的节点才有，到其他节点了，那么边就不同了（虽然是相同的对应节点名称，但是还是不同的类对象），再说，该边的next只是保存对应同一顶点的边的
        boolean b = false;

        public Vertex(String name, Edge next) {
            this.name = name;
            this.next = next;
        }

    }

    public class Edge {
        String name;
        int weight;
        Edge next;

        public Edge(String name, int weight, Edge next) {
            this.name = name;
            this.weight = weight;
            this.next = next;
        }


    }

    Map<String, Vertex> map;

    public test99() {
        map = new HashMap<>();
    }

    public void insertNode(String a) {

        if (map.get(a) == null) {
            Vertex aa = new Vertex(a, null);
            map.put(a, aa);
        }

    }

    public void insertEdge(String a, String b, int c) {

        Vertex vertex = map.get(a);
        if (vertex == null) {
            vertex = new Vertex(a, null);
            map.put(a, vertex);
        }


        if (vertex.next == null) {
            vertex.next = new Edge(b, c, null);
        } else {
            Edge temp = vertex.next;
            Edge temp2 = vertex.next;
            while (true) {
                //为了后续队列的操作，这里需要进行大小的判断，由于不用考虑头，所以代码相对简单

                //防止添加相同的边
                if (temp.name == b) {
                    temp.weight = c;
                    return;
                }

                if (temp.name.hashCode() > b.hashCode()) { //那么就说明新添加的比较小，所以对应的要放在前面
                    if (temp2 != vertex.next) {
                        //进入这里，说明他已经经历了一个循环
                        Edge j = new Edge(b, c, null);
                        temp2.next = j;
                        j.next = temp;
                    } else {
                        //进入这里，说明就是第一次
                        Edge j = new Edge(b, c, null);
                        vertex.next = j;
                        j.next = temp2;
                    }
                    return;
                }

                if (temp.next == null) {
                    temp.next = new Edge(b, c, null);
                    return;
                }
                //其他情况就是大的，当然，这里可以不用判断，因为外面就是大的了，虽然也可以判断，之前的链表操作就是判断的，这里就不判断了，反正是一样的
                temp2 = temp;
                temp = temp.next;
            }
        }

    }

    public void Select() {
        Set<Map.Entry<String, Vertex>> entries = map.entrySet();
        Iterator<Map.Entry<String, Vertex>> iterator = entries.iterator();
        while (iterator.hasNext()) {
            Map.Entry<String, Vertex> entry = iterator.next();
            Vertex vertex = entry.getValue();
            Edge edge = vertex.next;
            while (edge != null) {
                System.out.println(vertex.name + " 指向 " + edge.name + " 权值为：" + edge.weight);
                edge = edge.next;
            }

        }
    }

    //现在我们来编写广度优先搜索
    public void Select2(String a) {
        Set<String> strings = map.keySet();
        Iterator<String> iterator = strings.iterator();
        while (iterator.hasNext()) {
            String next = iterator.next();
            map.get(next).b = false;
        }
        String[] array = new String[map.size()];
        int i = 0;
        //首先得到该节点
        Vertex vertex = map.get(a);

        //定义一个队列
        Queue<String> queue = new LinkedList<>();
        queue.offer(vertex.name); //入队
        vertex.b = true; //设置标记
        //出队
        String poll = queue.poll();
        array[i] = poll;
        i++;

        while (true) {
            //操作入队
            Edge edge = vertex.next;
            if (edge != null) {

                while (edge != null) {
                    if (map.get(edge.name).b == false) {
                        queue.offer(edge.name);
                        map.get(edge.name).b = true; //标记
                    }
                    edge = edge.next;
                }


            }
            //最后一个出队也到这里，说明操作完毕
            if (queue.isEmpty()) {
                break;

            }
            //上面将相关的都入队后，然后外面操作出队，若没有入队的，那么自然是对应下一个出队
            String poll1 = queue.poll();

            array[i] = poll1;
            i++;

            vertex = map.get(poll1); //得到出队的顶点
            edge = vertex.next; //操作出队顶点的入队


        }
        //打印遍历的信息
        System.out.print("[");
        for (int ii = 0; ii < array.length; ii++) {
            if (ii == array.length - 1) {
                System.out.print(array[ii]);
            } else {
                System.out.print(array[ii] + ",");
            }
        }
        System.out.println("]");


    }
    //至此，广度优先遍历操作完毕

    //这里的代码我进行了没有必要的删除，因为深度（深度优先搜索）是不需要的，现在我们任然是编写一个方法，代码与前面的广度的代码基本类似
    //只是需要部分修改
    public void Select3(String a, String b) { //b代表终点
        Set<String> strings = map.keySet();
        Iterator<String> iterator = strings.iterator();
        while (iterator.hasNext()) {
            String next = iterator.next();
            map.get(next).b = false;
        }
        String[] array = new String[map.size()];
        int i = 0;
        //首先得到该节点
        Vertex vertex = map.get(a);

        //定义一个队列
        Queue<String> queue = new LinkedList<>();
        queue.offer(vertex.name); //入队
        vertex.b = true; //设置标记
        //出队
        String poll = queue.poll();
        array[i] = poll;
        i++;
        //定义最终的节点
        Vertex l = null;
        while (true) {
            //操作入队
            Edge edge = vertex.next;
            if (edge != null) {

                int o = 0;
                while (edge != null) {
                    if (map.get(edge.name).b == false) {

                        queue.offer(edge.name);
                        map.get(edge.name).b = true; //标记
                    }
                    map.get(edge.name).prev = vertex;
                    if (edge.name == b) {
                        l = map.get(edge.name);
                        o = 1;
                        break;
                    }
                    edge = edge.next;

                }
                if (o == 1) {
                    break;
                }


            }
            //最后一个出队也到这里，说明操作完毕
            if (queue.isEmpty()) {
                break;

            }
            //上面将相关的都入队后，然后外面操作出队，若没有入队的，那么自然是对应下一个出队
            String poll1 = queue.poll();

            array[i] = poll1;
            i++;

            vertex = map.get(poll1); //得到出队的顶点
            edge = vertex.next; //操作出队顶点的入队


        }
        //打印路径

        String[] aaa = new String[map.size()];
        int oo = 0;
        for (int ii = 0; ii < aaa.length; ii++) {
            aaa[ii] = l.name;
            oo++;
            l = l.prev;
            if (l == null) {
                break;
            }
        }
        //进行提取路径
        System.out.println(Arrays.toString(aaa));
        String[] bbb = new String[oo];
        for (int pp = 0; pp < bbb.length; pp++) {
            bbb[pp] = aaa[pp];
        }
        String[] ccc = new String[bbb.length];
        //因为他的路径是反的，所以再次的反过来
        for (int pp = 0, ss = ccc.length - 1; pp < ccc.length; pp++, ss--) {
            ccc[pp] = bbb[ss];
        }
        System.out.println("路径如下：" + Arrays.toString(ccc));

    }

    public static void main(String[] args) {
        test99 graph = new test99();
        graph.insertNode("A");
        graph.insertNode("B");
        graph.insertNode("C");
        graph.insertNode("D");
        graph.insertNode("E");
        graph.insertNode("F");


        //给c这个顶点，添加A这个顶点，对应的权值是1，后面依次类推即可
        graph.insertEdge("C", "A", 1);
        graph.insertEdge("F", "C", 2);
        graph.insertEdge("A", "D", 5);
        graph.insertEdge("A", "B", 4);
        graph.insertEdge("E", "B", 2);
        graph.insertEdge("D", "F", 4);
        graph.insertEdge("D", "E", 3);


        graph.Select();

        graph.Select2("A");
        graph.Select3("A", "E"); //[A, D, E]，这就是最短路径

    }

}
//从这里我们可以发现，对应的图的确是由顶点和边组，因为边也能够得到具体的顶点，当然如果他也是当前类，那么也是一样的得到，因为name的存在可以使得map来得到无论他是当前Vertex类（前面说明操作权重的是否需要相同类的哪个地方进行了说明，即"当然，你可能会问，设置相同的类不就好了，实际上也行"），还是定义的Edge类
//所以顶点的设计，以及边的设计，和集合的设计，都是有深意的

至此，对应的最短路径操作完毕

时间复杂度：

深度优先搜索的时间复杂度是：O（V+E），v代表边数（因为他的寻找就是根据边的），E代表节点数，也就是顶点数，因为我们还需要进行回退，即出栈，这个循环就是顶点数，那么可以同理，实际上广度优先搜索也是O（V+E），V也是边数，E也是顶点数

即深度优先遍历（搜索，是图的遍历或者搜索）和广度优先遍历（搜索，是图的遍历或者搜索）都是O（V+E）

上面忽略了打印的时间复杂度，否则还要加上O（X），X代表打印代码的执行次数

应用：

广度优先的搜索可以同时从起始点和终点开始进行，称之为双端 BFS，这种算法往往可以大大地提高搜索的效率

社交网络可以用图来表示，这个问题就非常适合用图的广度优先搜索算法来解决，因为广度优先搜索是层层往外推进的

首先，遍历与起始顶点最近的一层顶点，也就是用户的一度好友，然后再遍历与用户 距离的边数为 2 的顶点，也就是二度好友关系，以及与用户距离的边数为 3 的顶点，也就是三度好友关系，即就是这样的说明

算法思维 ：

接下来说明的都是思想，而不是算法，只是我们可以利用这些思想，可以更加合理的，或者简便的使用具体算法来实现需求

贪心算法 ：

概念 ：

贪婪（心）算法（Greedy）的定义：是一种在每一步选中都采取在当前状态下最好或最优的选择，从而希望导致结果是全局最好或最优的算法

贪婪算法：当下做局部最优判断，不能回退（能回退的是回溯，最优+回退是动态规划），注意：可能你认为是最好的，但是可能还有更好的，所以这里是看个人的最优判断

由于贪心算法的高效性以及所求得答案比较接近最优结果，贪心算法可以作为辅助算法或解决一些要求结果不特别精确的问题

注意：当下是最优的，并不一定全局是最优的，举例如下：

有硬币分值为10、9、4若干枚，问如果组成分值为18，最少需要多少枚硬币？

采用贪心算法，选择当下硬币分值最大的：10

注意：是当下最大的硬币，也就是说，必须先操作10，所以有如下：

18-10=8，8/4=2

即：1个10、2个4，共需要3枚硬币

但实际上我们知道，选择分值为9的硬币，2枚就够了（18/9=2），所以我们才会说贪心算法是当下最优解，而不是全局的

所以才会说明当下做局部最优判断，有时候也可以认为我们已经操作一部分了，那么现在最优解是什么，但是前面的部分未必是最优解的

如果改成：

有硬币分值为10、5、1若干枚，问如果组成分值为16，最少需要多少枚硬币？

采用贪心算法，选择当下硬币分值最大的：10

16-10=6

6-5=1

即：1个10，1个5，1个1 ，共需要3枚硬币

即为最优解，由此可以看出贪心算法适合于一些特殊的情况，如果能用一定是最优解（且是全局的，即当前就是在最好的情况下进行贪心）

总而言之，就是在一定情况下，做出最优解，而该情况可能是最好的状态，也可能是不好的状态，而贪心不能改变该情况，所以贪心可以是全局最优解，也可以是局部最优解，但是该情况是最好的情况比例是很少的，所以总体来说，贪心就称为局部最优解了（虽然他在极端情况下，也能是全局最优解），以后说明的最优解，我们统称为局部最优解，如果是全局最优解我会特殊说明

实际上从上面可以看出，三个硬币中，如果最大的硬币（10），与第二大的硬币（5或者9），相差很大，那么最优解就更加全局

当然，这不是贪心算法，而是上面说明的本身的情况，即状态，所以第二种有5的，就是最好的状态（当然，还有好的状态，或者不好的状态，我们一般也将不是最好的状态，称为不好的状态，因为局部最优解是全局最优解之外的统称）

经典问题：部分背包

背包问题是算法的经典问题，分为部分背包和0-1背包，主要区别如下：

部分背包：某件物品是一堆，可以带走其一部分

0-1背包：对于某件物品，要么被带走（选择了它），要么不被带走（没有选择它），不存在只带走一 部分的情况

部分背包问题可以用贪心算法求解，且能够得到最优解

以部分背包的问题为例子（作为主要的情况来操作，不是0-1背包的问题）：

假设一共有N件物品，第 i 件物品的价值为 Vi ，重量为Wi，一个小偷有一个最多只能装下重量为W的背包，他希望带走的物品越有价值越好，可以带走某件物品的一部分，请问：他应该选择哪些物品？

假设背包可容纳50Kg的重量，物品信息如下表：

贪心算法的关键是贪心策略的选择或者思考，比如如下策略的思考：

从上面可以看出，A的价值是最好的，因为换算成重量，那么就是最好的

我们可以将物品按单位重量所具有的价值排序，总是优先选择单位重量下价值最大的物品

按照我们的贪心策略，单位重量的价值排序： 物品A > 物品B > 物品C

因此，我们尽可能地多拿物品A，直到将物品A拿完之后，才去拿物品B，然后是物品C，很明显按照这样的顺序，物品C会只拿一部分，这样，可以使得得到最多的利润，而这样的想法也归属于贪心算法（或者称为贪心，或者称为贪婪，或者称为贪心算法）

具体代码如下，可以先看一下，然后自己进行编写：

package test;

/**
 *
 */
public class test1 {

    //这里我们定义一个类，来代表商品的关系（对象的概念）
    public static class Goods {
        String name; //物品名称
        double weight; //物品重量，实际上通常需要double来表示实际重量，因为在生活中都基本是有小数的
        double price; //物品价格
        String k = ""; //为了给不排序进行操作的变量
        //这里就不给出具体一千克多少元的变量了，因为实际上生活中，是需要我们自己计算的


        public Goods(String name, double weight, double price) {
            this.name = name;
            this.weight = weight;
            this.price = price;
        }
    }

    //既然类已经定义好了，那么我们在测试时，必然是需要操作三个他这个对象的，所以具体方法如下：
    //参数1：商品列表，我们通常需要将他进行排序，参数2：我们需要的最大重量，即背包最大重量
    public void take(Goods[] goods, double a) {
        //我们先对该列表进行排序，那么有个问题，可以不排序吗，并且，不排序的时间复杂度会低吗，在代码中，我会给出两种操作，一个是排序的，一个是不排序的
        //即在后面我会给出一个没有排序的方法，你可以进行对比，来观察时间复杂度
        //进行排序
        Goods[] sort = sort(goods);

        double j = 0;
        //我们来决定操作拿什么
        for (int i = 0; i < sort.length; i++) {
            //我们先判断我们的容量是否可以全部拿取
            if (a >= sort[i].weight) {
                a -= sort[i].weight;
                System.out.println(sort[i].name + "全部拿走，总共：" + sort[i].weight + "kg，总价值" + sort[i].price);
                j += sort[i].price;
            } else {
                //如果容量不能都进行拿取，那么只能是取一部分了
                System.out.println(sort[i].name + "部分拿走，总共：" + a + "kg，总价值" + a * sort[i].price / sort[i].weight);
                j += a * sort[i].price / sort[i].weight;
                a -= a;
                break;


            }

        }
        System.out.println("总共得到" + j + "元");
        System.out.println("背包剩余容量：" + a + "kg");


    }

    //如果不操作排序，那么需要如下代码：
    public void take1(Goods[] sort, double a) {

        double j = 0;
        //我们来决定操作拿什么
        for (int i = 0; i < sort.length; i++) {
            //找到最好的商品
            int ii = 0;
            Goods g = sort[ii];
            while (true) {
                if (ii + 1 >= sort.length) {
                    break;
                }
                if (g.k.equals("不存在")) {
                    g = sort[ii + 1];
                    ii++;
                    continue;
                }
                if (g.price / g.weight < sort[ii + 1].price / sort[ii + 1].weight) {
                    g = sort[ii + 1];

                }
                ii++;
            }

            //我们先判断我们的容量是否可以全部拿取
            if (a >= g.weight) {
                a -= g.weight;
                System.out.println(g.name + "全部拿走，总共：" + g.weight + "kg，总价值" + g.price);
                j += g.price;
            } else {
                //如果容量不能都进行拿取，那么只能是取一部分了
                System.out.println(g.name + "部分拿走，总共：" + a + "kg，总价值" + a * g.price / g.weight);
                j += a * g.price / g.weight;
                a -= a;
                break;

            }
            g.k = "不存在";


        }
        System.out.println("总共得到" + j + "元");
        System.out.println("背包剩余容量：" + a + "kg");


    }
    //我们可以发现，他里面嵌套了循环，那么他最少也是n^2，而不排序的基本是n^2+n（虽然有优化）
    //即，我们可以发现，不排序的时间复杂度竟然比较低，所以有时候我们并不会必须排序，我们通过观察可以发现，实际上是因为先排序的，他需要保存，而不排序的直接使用了，所以减少了保存的时间复杂度，也就是n
    //但是，不排序的真的好吗，答：在非常多的操作中，我们最好进行排序，虽然这里他看起来不排序的好，那么如果后面又有一个操作，比如我需要你输出从大到小的对应每1kg多少元，很明显，他要进行循环，是n^2，而先排序的，只需要一个循环即可，即O（n），所以这个时候，排序的就只需要n^2+2n，但是不排序的却需要2n^2，很明显，如果n是2，那么自然相等，但是一般n都是有很多的，所以通常来说排序的好，即我们通常会使用排序的
    //所以实际上先排序的可以重复利用，只是他的一开始需要更多的时间复杂度而已

    //那么结合上面的，我们知道，排序的可以重复利用，那么我们可以选择忽略排序的时间复杂度（只是这里，其他地方要的话，我们通常不会忽略）
    //那么该贪心算法的（该操作），只需要O（n）即可，n是商品数量


    //定义排序方法
    public Goods[] sort(Goods[] a) {
        //根据需求，排序是需要根据其重量对应的元来进行的，根据前面学习的排序，这里我们使用冒泡排序，因为最简单，虽然时间复杂度比较高
        for (int i = 0; i < a.length - 1; i++) {
            boolean is = true;
            for (int j = 0; j < a.length - 1 - i; j++) {
                Goods tmp = null;
                if ((a[j].price / a[j].weight) < (a[j + 1].price / a[j + 1].weight)) {
                    is = false;
                    tmp = a[j];
                    a[j] = a[j + 1];
                    a[j + 1] = tmp;
                }
            }

            if (is) {
                break;
            }
        }
        return a;

    }

    public static void main(String[] args) {
        test1 bd = new test1();
        Goods goods1 = new Goods("A", 10, 60);
        Goods goods2 = new Goods("B", 20, 100);
        Goods goods3 = new Goods("C", 30, 120);
        Goods[] goodslist = {goods1, goods2, goods3};
        bd.take(goodslist, 50);
        bd.take1(goodslist, 50);

    }
}

时间复杂度 ：

在不考虑排序的前提下（省略了n^2），贪心算法只需要一次循环，所以时间复杂度是O（n），n是商品数量

优缺点：

优点：性能高，能用贪心算法解决的往往是最优解

缺点：在实际情况下能用的不多，用贪心算法解的往往不是最好的，需要自己的逻辑思维，所以贪心算法往往不能求得最优解

所以，实际上得到最优解的解决方案（看起来，并不是一定是最优解，后面会说明，比如斐波那契数列的通项公式），我们都会认为是贪心算法，当然上面只是一种思维，即我们需要得到最好的，那么就可以认为是贪心算法

适用场景 ：

若针对一组数据，我们定义了限制值和期望值，我们希望从中选出几个数据，在满足限制值的情况下，使得期望值最大

或者说每次选择当前情况下，在对限制值同等贡献量的情况下，对期望值贡献最大的数据（局部最优，也可以使得全局最优）

上述情况，大部分能用贪心算法来解决问题

贪心算法的正确性都是显而易见的，也不需要严格的数学推导证明，在实际情况下，用贪心算法解决问题的思路，并不总能给出最优解（特别是全局，因为比例太少，部分局部也不能，比如其对应可以通过数学知识，比如斐波那契数列的通项公式，他是最优解，而贪心算法在对应情况下，是基本得不到比他还要好的最优解的）

简单来说，贪心算法是使得在当前情况下是最优解的思想，只有你认为是最优解的即可，无论是否有其他最优解（比如斐波那契数列的通项公式，他这种情况，单纯的使用贪心算法思想，可能是想不到的），即贪心算法是一种思想，而不是一个算法，只是这个思想形成的算法，我们称为贪心算法

分治算法：

概念 ：

分治算法（divide and conquer）的核心思想其实就是四个字，分而治之 ，也就是将原问题划分成 n个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，就得到原问题的解（快速排序就是一种使用了分治法，即分治算法的排序）

关于分治和递归的区别：

分治算法是一种处理问题的思想，递归是一种编程技巧，分治算法的递归实现中，每一层递归都会涉及这样三个操作：

分解：将原问题分解成一系列子问题 （调用自身，相当于递归三要素中的"函数的功能 "，虽然他可以看成就是相当于递归）

解决：递归地求解各个子问题，若子问题足够小，则直接求解 （有最终返回条件，即终止条件，相当于递归三要素中的"函数的功能加上递归结束条件"）

合并：将子问题的结果合并成原问题（相当于递归三要素中的"函数的等价关系式"，虽然这里不同的是，他是主要操作合并的，而并不会必须是一个关系式，只需要是一个方程或者具体式子操作即可）

可以看到，实际上分治算法基本需要利用递归，但是并不完全需要递归，虽然递归的具体操作是正好符合他分治的思想而已，但是也可以使用其他方式，比如循环（如快速排序），只要思想是这样的即可，所以上面我才会说"分治算法是一种处理问题的思想，递归是一种编程技巧"，只不过该技巧，符合他的主要操作（分治），就如循环是实现次数，而递归是调用自身，但是像这些操作，我们都称为技巧（也是算法，只不过这些大众认为的基本操作，我们也称为技巧而已，像前面的"跟踪算法"，以及"定义临时变量"等等都是技巧，虽然也称为算法，只是大多数这样操作能够更好的进行实现具体要求，我们也通常会利用这些技巧来更好的实现具体需求）

比如：

将字符串中的小写字母转化为大写字母

“abcde"转化为"ABCDE”

我们可以利用分治的思想将整个字符串转化成一个一个的字符处理

经典问题 ：

上述问题代码如下，可以先看一下，然后自己编写：

package test;

/**
 *
 */
public class test2 {

    //定义变大写的方法
    public static char toUpCaseUnit(char c) {
        //因为在ASCII中，a代表97，z代表122，所以，如果对应的字母越界了，那么直接的返回空字符（没有''），字符必须要有个值
        int n = c;
        if (n < 97 || n > 122) {
            return ' ';
        }
        //如果在该范围里面那么减去32即可
        return (char) (n - 32);
    }

    //定义了对应的转换，那么我们来操作他
    //参数1：代表对应的字符串的字符，因为这里是递归，所以需要有对象操作（数组），来使得递归的方法也能继续操作
    //参数2：代表从哪个下标开始进行变大，下标自然包括0
    public static char[] toUpCase(char[] chs, int i) {
        if (i >= chs.length) return chs; //如果超过了，说明没有什么需要进行变大的，自然返回自身
        chs[i] = toUpCaseUnit(chs[i]); //将该字符进行变大
        return toUpCase(chs, i + 1); //重新执行当前方法，该就是式子操作，而并非一定是关系式
        //很明显，他最终都会返回return chs，即当前数组
        //实际上我们也可以使用循环来操作
    }

    //实际上我们也可以使用循环来操作
    //具体方法如下
    public static char[] toUpCase1(char[] chs, int i) {
        for (int a = i; a < chs.length; a++) {
            chs[a] = toUpCaseUnit(chs[a]);
        }
        //都进行变大后，直接的退出，不用考虑判断了
        return chs;
    }

    public static void main(String[] args) {
        String ss = "abcde";
        System.out.println(test2.toUpCase(ss.toCharArray(), 0));
        System.out.println(test2.toUpCase1(ss.toCharArray(), 0));
    }

}

时间复杂度：就是字符串的长度，也就是O（n）

求X^n问题：

比如：2^10，即2的10次幂

一般的解法是循环10次

package test;

/**
 *
 */
public class test3 {
    public static int commpow(int x, int n) { //假设x是2，n是10
        int s = 1;
        while (n >= 1) { //因为n是10，所以这里会执行10次
            s *= x; //执行10次，那么会乘以10个2，也就是2^10了
            n--;
        }
        return s;
    }

    public static void main(String[] args) {
        System.out.println(commpow(2, 10));
    }
}

该方法的时间复杂度是：O（n），n代表多少次幂

采用分治法：

2^10拆成：

我们看到每次拆成n/2次幂，时间复杂度是O（logn），可能你看不明白，没有关系，看代码就知道了：

package test;

/**
 *
 */
public class test4 {
    public static int dividpow(int x, int n) { //假设x是2，n是10
        //递归结束 任何数的1次方都是它本身
        if (n == 1) {
            return x;
        }
        //每次分拆成幂的一半
        int half = dividpow(x, n / 2); //很明显，他里面会操作其一般的次幂
        //偶数
        if (n % 2 == 0) {
            return half * half;
        } else {
            return half * half * x;
        }
    }

    //看代码，你可能很难看出，现在，我给出具体的流程
    //当2，10进入后
    /*
    2，10进入的half等待获取值，2，5进入后等待获取值，2，2进入后等待获取值，2，1进入后，返回一个2
    2，2，得到该2，返回2*2
    2，5，得到2*2，返回（2*2）*（2*2）*2
    2，10，得到（2*2）*（2*2）*2，返回（2*2）*（2*2）*2*（2*2）*（2*2）*2，即2^10，至此方法真正的结束
    所以上面的：
    if (n % 2 == 0) {
            return half * half;
        } else {
            return half * half * x;
        }
        就是操作其次幂，这里你最好多思考一下
        实际上是因为底层最里面的原因，导致2这个值一直返回，而其上面的都操作返回的值，而因为奇数的存在，所以导致奇数需要多出来一个2
        至此，底层的原因说明完毕，具体如何体会，看你自己吧
     */
    public static void main(String[] args) {
        System.out.println(dividpow(2, 10));
    }
}

//上面是从低到高的进行说明该算法，现在你再看看之前的图片，可以发现，实际上他的每一次操作，都会结合返回值来进行重合，即从高到低的进行说明
//所以就会出现前面图片的情况，因为加起来的half就是前面的图片最后的组合

时间复杂度：

根据拆分情况可以是O（n）或O（logn），为什么可以是O（n），因为如果对应只需要2^1，那么难道不是O（n）吗，当然，这是极端情况下的，因为按照这样说，那么所有的O（logn）的操作都基本可以是O（n），所以总体来说，我们就认为他是O（logn），即不考虑极端情况，除非具体说明（比如这里就说明了），因为"时间复杂度是整体的说明的，而不是投机取巧说明的"（前面说明过了）

优缺点：

优势：将复杂的问题拆分成简单的子问题，解决更容易，另外根据拆分规则，性能有可能提高

劣势：子问题必须要一样，用相同的方式解决（因为是相同的方法，即利用自己）

适用场景 ：

分治算法能解决的问题，一般需要满足下面这几个条件：

原问题与分解成的小问题具有相同的模式（相同的自身方法）

原问题分解成的子问题可以独立求解，子问题之间没有相关性，这一点是分治算法跟动态规划的明显区别

具有分解终止条件，也就是说，当问题足够小时，可以直接求解（即前面说明的返回2）

可以将子问题合并成原问题，而这个合并操作的复杂度不能太高（即前面说明的判断），否则就起不到减小算法总体复杂度的效果了

回溯算法 ：

概念：

回溯算法实际上一个类似枚举的深度优先搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发 现已不满足求解条件时，就"回溯"返回（也就是递归返回），尝试别的路径（虽然可能该路径已经确定，但还是会检验的）

回溯的处理思想，有点类似枚举（列出所有的情况）搜索，我们枚举所有的解，找到满足期望的解，为了有规律地枚举所有可能的解，避免遗漏和重复，我们把问题求解的过程分为多个阶段，每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走，人生如果能够回退？那么你想回退到哪个阶段呢？

经典问题 ：

N皇后问题：

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击

我们把这个问题划分成 8 个阶段，依次将 8 个棋子放到第一行、第二行、第三行…直到第八行

在放置的过程中，我们不停地检查当前放法，是否满足要求，如果满足，则跳到下一行继续放置棋子，如果不满足，那就再换一种放法，继续尝试（这里就使用了回溯的思想，具体如何使用，我们在代码中进行查看）

具体实现代码如下（可以先看下，然后自己进行编写）：

package test;

/**
 *
 */
public class test5 {
    //皇后，在上下直线以及其四个方向的对角线都能进行攻击（具体百度查看即可），所以这里要考虑这些情况

    //要解决n皇后的问题，我们知道，要添加皇后时，他的主要问题是在添加这个皇后之后，其他的皇后不能在他的对角线上（斜线）以及直线上
    //那么如何操作对角线和直线呢，且加上皇后之后，那么后面每次添加皇后，都必须要前面的皇后进行判断，这非常困难

    //当然，虽然很困难，但是还是可以操作的，话不多说，先看代码，在代码中进行说明

    //首先我们先定义皇后数量，我们将棋盘从0开始，到7就行（行和列都是这样），那么棋盘最大数量的皇后必然只能是8个，因为对角线和直线的存在，所以皇后只能是8个（主要是因为直线）
    static int QUEENS = 8;
    //那么如何定义棋盘的，由于皇后是8个，那么整个棋盘中，其中一行也只能是一个（直线只能存在一个皇后），即很明显，我们可以定义一个数组即可
    int[] result = new int[QUEENS]; //我们将下标表示行，里面的值表示存储在哪一列即可（这里是覆盖的必然条件，在后面会有解释为什么要这样）

    //定义多少可能
    int aa = 0;

    //定义执行次数
    int jj = 0;

    //现在，我们以及定义好棋盘了，那么现在我们来编写主要代码：
    //首先是存放皇后的位置，参数a代表要添加的行
    public void insert(int a) {

        //这里我会使用递归来操作，当然，如何操作看后面即可
        //首先操作结束条件
        if (a >= QUEENS) { //只要==即可，但为了以防万一（一般是高并发才会出现"万一"的情况，即出现问题，那么在高并发下，我们最好设置>=，这里可以只要==即可，反正基本不会出现什么问题），这里设置>=
            printQueens(); //添加完毕，才会操作打印，这里的理解，也要看后面
            aa++;
            return;
        }
        //现在，我们来进行放入皇后
        for (int i = 0; i < QUEENS; i++) { //这个i代表列，那么自然这个列不能超过8
            //System.out.println("执行第" + ++jj + "次循环"); //这里的+要进行分开，否则会报错，比如：因为不知道是+（连接）还是++（操作值的加1）
            //++jj;
            if (isOK(a, i)) { //判断是否可以放置，即在该行和该列是否可以放置
                //如果可以放置，那么我们进行放置
                result[a] = i;//该行的该列（值）
                //开始下一行
                insert(a + 1);
                //这里我会进行大致说明：
                //加上了这个，代表我们已经操作完毕，为什么，这里你仔细思考一下回溯
                //如果我们这里添加成功一次，那么当insert(a+1);返回后
                //其他的循环，是不是必然直接的跳过，而不会操作isOK(a,i)为true，答：不是，如果是上面的，必然会导致在这种情况下，出现问题：
             /*


                1 0 0 0 0 0 0 0
                0 0 1 0 0 0 0 0
                0 0 0 0 1 0 0 0
                0 1 0 0 0 0 0 0
                0 0 0 1 0 0 0 0
                0 0 0 0 0 0 0 0 在这一行，我们可以发现，他必然是添加不了的，也就是说，他会往上走，当然，我们判断isOK中，判断是是竖直的直线，所以这里会延续其列
                0 0 0 0 0 0 0 0
                0 0 0 0 0 0 0 0

                会改变其该列，即变成了
                1 0 0 0 0 0 0 0
                0 0 1 0 0 0 0 0
                0 0 0 0 1 0 0 0
                0 1 0 0 0 0 0 0
                0 0 0 0 0 0 0 1 因为只有一个列，所以数组覆盖后，那么就变成了这里
                0 0 0 0 0 0 0 0
                0 0 0 0 0 0 0 0
                0 0 0 0 0 0 0 0
                当然有很多种这样的情况，但是无论你怎么存放，对角线都充足的，所以通过上面的操作，必然会导致一个结果出来，这里的最终结果是：
                0 0 0 0 0 0 0 1
                0 0 0 1 0 0 0 0
                1 0 0 0 0 0 0 0
                0 0 1 0 0 0 0 0
                0 0 0 0 0 1 0 0
                0 1 0 0 0 0 0 0
                0 0 0 0 0 0 1 0
                0 0 0 0 1 0 0 0

                你可能会有疑惑，这样也行啊：
                1 0 0 0 0 0 0 0
                0 0 0 0 1 0 0 0
                0 0 0 0 0 0 0 1
                0 0 0 0 0 1 0 0
                0 0 1 0 0 0 0 0
                0 0 0 0 0 0 1 0
                0 1 0 0 0 0 0 0
                0 0 0 1 0 0 0 0
                但是打印信息为什么会有多个
                这里就要格外考虑了：
                我们查看上面的这个代码：
                 if (a == QUEENS) {
                    printQueens(); //添加完毕，才会操作打印，这里的理解，也要看后面
                    return;
                }
                我们可以发现，当全部满足时，可以进行返回，但是你要知道，他的满足中，前面的路径是可以改变的，因为不会判断水平和左下角和右下角，比如其中第一行的位置是能够再次的覆盖移动，通过这样的说明你应该可以发现，他就是打印出所有的情况
                以第一行为主（因为是查看左上角和右上角的，而不会查看左下角和右下角的），其他行满足前面的行时，慢慢的往下制造打印的可能，然后可以改变前面的行，然后如此反复，自然就是打印所有情况，即这的确利用的回溯的本意"我们枚举所有的解，找到满足期望的解，为了有规律地枚举所有可能的解，避免遗漏和重复，我们把问题求解的过程分为多个阶段，每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走"
                即可以这样的认为，如果是：
                "111"数字
                让你列举111到999的所有的可能，那么自然是112，113，当119后，然前一个进行加1，这就是回溯的一个意思，上面的n皇后也是利用这样，当后面的完全满足时，或者到尽头了，那么前面的可以进行移动了
        */
                //这是因为数组的特性（对同一个下标进行更新，那么就相当于覆盖操作了），所以可以这样的覆盖，所以在isOK中，我才说，数组隐含的表示了水平，也就是说，实际上我们也判断了其他的可能，即回溯了，也检验了"枚举所有的解"，避免遗漏和重复
                //即检验了上一个的不是吗，所以在回溯的介绍中，我们也说明了"当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走"
                //所以与递归不同的是，他的返回是能够在上一个继续的递归，而不是返回后，继续在上一个去返回，这就是回溯的基本思想

            }
            //如果不可以放置，那么在该行的其他列进行放置，因为其直线和对角线的原因，实际上必然可以放置8个（因为对角线是大于8的，即有15个，才能全部覆盖，但只能添加8个，因为直线的原因，即直线决定上下和位置，对角线只决定位置）

            //至此，只有对应的所有循环都结束，那么打印才会结束，即代码执行完毕

        }

    }

    public void printQueens() {
        for (int i = 0; i < QUEENS; i++) { //定义行
            System.out.print("|");
            for (int j = 0; j < QUEENS; j++) { //定义列
                if (result[i] == j) {
                    System.out.print("Q|");
                } else {
                    System.out.print("*|");
                }
            }
            System.out.println(); //换行
        }
        System.out.println("-----------------------");

    }

    //这里是n皇后的主要问题，用来确定是否在对角线或者直线上有皇后
    public boolean isOK(int a, int b) { //参数a代表该行，b代表该列，我们主要的就是判断该行该列的对角线或者直线上是否有皇后
        int left = b - 1; //既然是对角线，那么首先线得到左边的对角线的第一个位置列
        int right = b + 1; //得到右边对角线的第一个位置列
        //那么我们是看上面的对角线，还是看下面的对角线呢（对角线有四个方向），答：我们只需要看上面的对角线，因为我们是往下添加的（即我们只看左上和右上），因为下面必然是没有皇后的（我们才刚刚添加，即尾部行添加，那么自然下面的行没有皇后）
        //那么我们就逐级的判断上一行即可
        int o =jj;
        for (int i = a - 1; i >= 0; i--) { //先从当前的上一行开始，然后依次的判断上面其他的行
            ++jj;
            //首先看他有没有在当前直线上（竖直的直线，因为水平的直线，已经通过数组隐含的表示了，在上面回溯中会说明，即上面的"这里你仔细思考一下回溯"那个地方）是否有皇后，因为这也是需要判断的（即这里补充）
            if (result[i] == b) { //如果上一行的值（也就是列，这个下标是行），与当前的列（值）相同，代表是一个直线
                return false; //返回false，代表有皇后
            }
            //查看左上角是否有皇后
            if (left >= 0) { //自然不能超过棋盘，否则是默认不存在皇后的，自然不会对该情况操作出返回false，相当于在最左边添加，那么自然不用考虑左边的对角线
                if (result[i] == left) { //若对应上一行的值等于该列（下标是代表行的，值是代表列的），那么说明对角线有皇后，即返回false
                    return false;
                }
            }
            if (right < QUEENS) { //与上面同理，这里没有=，当然加上也没有事情，因为列的值是不可能是QUEENS的，如果操作等于，那么在最右边添加，那么等于=就会出现对应的操作（与上面的在最左边添加相反）
                if (result[i] == right) {
                    return false;
                }

            }


            //如果没有返回，说明该两个位置列判断完成，那么我们再次的移动列
            left--;
            right++;

        }
        if(o==jj){
            jj++; //操作这个最终的jj是40290，因为外循环本身也算，和内循环结合也算一起（因为也是一起的）
        }
        //当上面的对角线和直线都判断没有皇后，那么说明该行和该列可以添加，自然返回true
        return true;

    }

    public static void main(String[] args) {
        test5 queens = new test5();
        queens.insert(0); //从0行开始添加
        System.out.println("有" + queens.aa + "个可能"); //92个可能
        System.out.println("执行了" + queens.jj + "次循环"); //40282次循环（实际上总共是40290，因为会第一行是直接跳过的，但是有8次操作，如果操作了上面的o==j就是40290），而8的阶乘是40320
        //这个次数有外面的循环和内循环总体来的
        //但也可以大致的认为是8的阶乘
        //当然，你可以设置对应的QUEENS=4，会发现，只有2个可能，但有78次循环
        //而4*3*2*1=24，比较多了，而对于3来说是没有可能的，即0个可能
        //你可能会有疑惑，按道理来说无论是设置8还是4，应该是阶乘的次数，但是为什么不是呢
        //现在我们来进行调试，很困难哦
    
        /*
        //现在就是第一次：
        1 0 0 0
        0 0 0 0
        0 0 0 0
        0 0 0 0
        
        1 0 0 0
        0 0 1 0 到这里，需要3次
        0 0 0 0
        0 0 0 0
        
        1 0 0 0
        0 0 1 0
        0 0 0 0 因为2+1+1+1=5次
        0 0 0 0
        
        1 0 0 0
        0 0 0 1 再来1次，那么这里的4次操作完毕，现在总共是10次了（包括该1次）
        0 0 0 0
        0 0 0 0
        
        1 0 0 0
        0 0 0 1
        0 1 0 0 总共需要2+2=4次
        0 0 0 0
        
        1 0 0 0
        0 0 0 1
        0 1 0 0
        0 0 0 0 需要1+1+1+2=5次，现在是19次了
        
        1 0 0 0
        0 0 0 1
        0 1 0 0 这里往后移动需要1+1=2次，即21次
        0 0 0 0
        
        经过21次后
        1 0 0 0
        0 0 0 0 由于他的执行是直接的退出，那么可以发现，上面的1需要移动
        0 0 0 0
        0 0 0 0
        至此，第一行的1代表21次，很明显，与你认为的4*4*4=64少很多次数
        现在我们来分析上面的情况，我们先看第二行，他总共执行次数是4，没有问题
        第三行就有问题了，即5+4+2=11次，从这里你应该可以看出，并不是每一次的上一行都会使得下一行进行操作，比如第二行只有两次会影响下一行，所以4*4*4*4是不正确的，而（3*1）*（2*1）*（1*1）*4=3*2*1*4（第一行操作4次），即认为他们只判断1次，这也是不正确的（因为有些执行2次，有些执行1次就退出），很明显，次数在他们中间，因为他们始终进行变化，所以需要需要考虑边界的问题，所以需要的次数在4*3*2*1<x<4*4*4*4（x是需要的次数）
        至此，他并没有什么规律，所以时间复杂度模糊不定（因为对角线和直线的存在是变化的，因为可以放在最左边和最右边，使得只有两个一次，而不是三个，或者导致只有少的次数影响下一行，所以模糊不定），但是我们认为他是按照理想情况下的最小进行操作，所以我们也认为这里的时间复杂度是n!，即4*3*2*1
        
        
        */
    }


}

至此n皇后说明完毕

时间复杂度：

N皇后问题的时间复杂度为：如果不考虑他的n皇后的本来意义，一般就是O（n^n），若考虑的情况下，我们可以认为是（n!，前面有解释，这里是相乘的阶乘，而不是相加，可能在某些优化下可以达到，并且可能也会可以是n!/2，具体优化可以百度查看）

在程序里面我们一般会将阶乘称为相加或者相乘，一般我们会认为是相乘（而不是相加，当然，在程序里面我们都可以表示，看情况即可）

优缺点：

优点：

回溯算法的思想非常简单，大部分情况下，都是用来解决广义的搜索问题，也就是，从一组可能的解 中，选择出一个满足要求的解

回溯算法非常适合用递归来实现，在实现的过程中，剪枝操作是提高回溯效率的一种技巧（相当于前面冒泡中的优化，比如其设置标志isSort），利用剪枝，我们并不需要穷举搜索所有的情况，从而提高搜索效率

劣势： 效率相对于低（动态规划）

适用场景 ：

回溯算法（思想）是个"万金油"，基本上能用的动态规划、贪心解决的问题，我们都可以用回溯算法解决

回溯算法相当于穷举搜索，穷举所有的情况，然后对比得到最优解，不过，回溯算法的时间复杂度非常高

是指数级别的，只能用来解决小规模数据的问题，对于大规模数据的问题，用回溯算法解决的执行效率 就很低了

动态规划 ：

概念：

动态规划（Dynamic Programming），是一种分阶段求解的方法

动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治） 的方式去解决

首先是拆分问题，我的理解就是根据问题的可能性把问题划分成一步一步这样就可以通过递推或者递归来实现

关键就是这个步骤，动态规划有一类问题就是从后往前推的

有时候我们很容易知道，如果只有一种情况时，最佳的选择应该怎么做，然后根据这个最佳选择往前一步推导，得到前一步的最佳选择 （也类似于该方法的编写，类似于包含递归三要素中的"函数的功能"和"递归结束条件"的作用）

然后就是定义问题状态和状态之间的关系，我的理解是前面拆分的步骤之间的关系，用一种量化的形式表现出来，类似于高中学的推导公式，因为这种式子很容易用程序写出来，也可以说对程序比较亲和（也就是最后所说的状态转移方程式，类似于递归三要素中的"函数的等价关系式"，虽然他并不是一定是关系式，但包含关系式）

我们再来看如下说明，我的理解是比如我们找到最优解，我们应该讲最优解保存下来：

为了往前推导时能够使用前一步的最优解，在这个过程中难免有一些相比于最优解差的解，此时我们应该放弃

只保存最优解，这样我们每一次都把最优解保存了下来，大大降低了时间复杂度（如后面斐波那契数列的备忘录操作，虽然他本来就是计算，单纯的计算自然归属于最优解，就比如23=6，你在再怎么操作，2 * 3=6就是最优解的，可能有与他同级，但基本不会超过（因为是自己的），比如32=6，当然，这个最优解是自己的最优解，不是别人的，因为6也可以是1 *6=6，这里以自己的最优解来说明）

动态规划中有三个重要概念：

1：最优子结构（类似于递归三要素中的"函数的功能"，但还是有点差别，可以说是最大的情况）

2：边界（类似于递归三要素中的"递归结束条件"）

3：状态转移公式（也可叫做递推方程），即dp方程（类似于递归三要素中的"函数的等价关系式"，一般来说递推就是循环操作的分解的递归，比如前面使用循环解决的斐波那契数列就是递推操作，所以递推方程和递归方程是类似的，而之所以分为递归和递推，主要是调用自身是归的意思，所以我们称为递归，而一路执行是推的意思，所以我们称为递推）

要注意，该dp方程可以是多样的，而不仅仅只是一个函数的关系式，特别在后面0-1背包问题中的分析会说明

经典问题 ：

再谈斐波那契数列：

优化递归：

通过上边的递归树可以看出在树的每层和上层都有大量的重复计算，可以把计算结果存起来，下次再用的时候就不用再计算了，这种方式叫记忆搜索，也叫做备忘录模式（前面有大致说明，在这个地方"缺点：占用空间较大、如果递归太深，可能会发生栈溢出、可能会有重复计算，可以通过备忘录（动态规划，在说明动态规划时会说明）或递归的其他方式去优化"）

现在我们来进行实现，可以先看一下，然后自己进行编写：

package test;

/**
 *
 */
public class test6 {
    //用于存储每次的计算结果
    static long[] sub = new long[100];

    public static long fib(int n) {
        if (n <= 1) return n;
        //没有计算过则计算

        if (sub[n] == 0) {
            sub[n] = fib(n - 1) + fib(n - 2); //之前的递归，基本是直接的返回该值，现在我们直接的保存
        }
        //计算过直接返回
        return sub[n];
    }

    //之前的代码
    public static long fa(int n) {
        if (n <= 1) return n;

        return fa(n - 1) + fa(n - 2);
    }


    public static void main(String[] args) {
        System.out.println(fib(50)); //50的话就是96次操作（调用自身）
        //可以发现，他的执行出现的结果比之前的快了很多（也就是下面的打印中使用的方法，就是之前的）
        System.out.println(fa(50)); //50的话就是96次，这个说明在下面的解释中
    }


}

dp方程：

/*
如果i<=1，那么dp[0]=0，dp[1]=1，dp代表上图中下面的类似数组
如果i>1，那么就是dp[i]=dp[i-1]+dp[i-2]，这就是dp方程
最优子结构：如果我们查询的是第9个下标，那么就是fib[9]=fib[8]+fib[7]，即最大的情况（也是函数的功能，因为的确要这样加）
边界：a[0]=0; a[1]=1;，可以看到的确类似于结束条件
dp方程：fib[n]=fib[n-1]+fib[n-2]
我们也可以发现，实际上算法的思想，基本都与递归有关，当然，虽然是不同的思路，可以具体的意义不同，侧重点不同
贪心侧重于当前（直接的解决即可，看最好情况）
分治侧重于下一个（子问题，相当于递归）
回溯侧重于上一个（使用循环来操作上一个）
而动态规划侧重于所有情况，通常我们也用来保存最优解（主要侧重）
他们基本都利用了递归

所以说，当某些问题需要你使用上面的情况时，自然是需要你进行侧重点进行出发
*/

现在我们来编写一个递推的代码（比上面的递归要好，在斐波那契数列中，递推是基本比递归好的，你可以设置在其中进行打印数字，每打印一次，该数字加1，这样来进行验证，很明显，可以发现，上面的递归需要96次，而下面的递推只需要49次），可以自己先看一下，然后编写：

package test;

/**
 *
 */
public class test7 {
    public static int fib(int n) {
        int a[] = new int[n + 1];
        a[0] = 0;
        a[1] = 1;
        int i;
        // a[n]= a[n-1]+a[n-2]
        for (i = 2; i <= n; i++) {
            a[i] = a[i - 1] + a[i - 2];

            //直接得到上一个
        }
        // i已经加1了，所以要减掉1
        return a[i - 1];
    }

    //之前的循环是：
    public static int fa(int i) {
        if (i <= 1) return i;
        int a = 0;
        int b = 1;
        for (int j = 2; j <= i; j++) {
            b = b + a;
            a = b - a;
            //进行移动

        }
        return b;
    }

    //很明显，上面的保存是按照数组来保存的，因为循环下标（参数）正好可以对应数组下标
    //这里稍微思考一下就是：
    //0 1 1 2 3，要得到5
    //前面的一种是，将数组对应下标的2的值和3的值相加到上一个下标（因为会有上一个，所以长度要比传递进来的参数要加1
    //而后面的一种就是2加上3，然后移动b到5，a到3

    public static void main(String[] args) {
        System.out.println(fib(9)); //50的话就是49
        System.out.println(fa(9)); //50的话就是49
    }

}

使用动态规划四个步骤：

1：把当前的复杂问题转化成一个个简单的子问题（分治）

2：寻找子问题的最优解法（最优子结构）

3：把子问题的解合并，存储中间状态（这是主要的思想，因为其他的基本于分治类似，因为分治相当于递归，即这里是主要的区别）

4：递归+记忆搜索或自底而上的形成递推方程（dp方程）

时间复杂度 ：

新的斐波那契数列（这里是递推的实现方式）实现时间复杂度为O（n）（以递推为例子则是O（n），因为是循环，前面第一次说明斐波那契数列时，就已经说明过了），n代表：你要找的数减去1

优缺点 ：

优点：时间复杂度和空间复杂度都相当较低

缺点：难，有些场景不适用

适用场景 ：

尽管动态规划比回溯算法高效，但是，并不是所有问题，都可以用动态规划来解决

能用动态规划解决 的问题，需要满足三个特征，最优子结构、无后效性和重复子问题

在重复子问题这一点上，动态规划 和分治算法的区分非常明显，分治算法要求分割成的子问题，不能有重复子问题

而动态规划正好相反（因为保存的存在操作，使得不用再次的计算了），动态规划之所以高效，就是因为回溯算法（因为也是单纯使用分治算法）实现中存在大量的重复子问题

数据结构与算法实战：

接下来给出几个问题来练一练手：

环形链表问题：

给定一个链表，判断链表中是否有环，存在环返回 true ，否则返回 false（头节点为null，也是这个）

分析：

该题可以理解为检测链表的某节点能否二次到达（重复访问）的问题，需要一个容器记录已经访问过的节点，每次访问到新的节点，都与容器中的记录进行匹配，若相同则存在环，那么直接的返回false，若匹配之后没有相同节点，则存入容器，继续访问新的节点，直到访问节点的next指针返回null，那么返回true，至此操作结束，实现简单

时间复杂度为：

遍历整个链表，即O（n），每次遍历节点，再遍历数组进行匹配，O（x），x代表总遍历数组的记录，如果是哈希的操作，那么只需要O（n）即可

这样就不用遍历了，而使得总时间复杂度是n+x（该x是（n-1+1）（n-1）/2=（n^2-n）/2，因为假设是9个节点，那么需要判断从1次到8次为止）

换个思路： 该题可以理解为"追击相遇"问题，如果存在环，跑得快的一定能追上跑得慢的，比如：一快一慢两个运动员，如果在直道赛跑，不存在追击相遇问题，如果是在环道赛跑，快的绕了一 圈肯定可以追上慢的

解法：

/*
1：定义快慢两个指针：
slow=head; 
fast=head.next; 
2：遍历链表（这里不考虑哈希的操作）：
快指针步长为2：fast=fast.next.next; 
慢指针步长为1：slow=slow.next;
3：当且仅当快慢指针重合(slow==fast)，有环，返回true
4：快指针为null，或其next指向null，没有环，返回false，操作结束
那么要不要考虑环的大小，答不用考虑，如果存在环，说明他们的移动必然会导致相同
那么为什么设置快的为2，可以设置3，4，5吗，最好不要，因为我们是需要注意fast.next.next中next是否为null的情况
那么如果解决这个问题，那么可以随便移动快的位置吗，答：可以
你可能会认为出现这样的
假设是：1 2 3 4 5，5指向3，我们设置快指针是4，首先假设快的先操作，那么直接到5，慢到2
以此类推：3 3，4 4，重合了，这一个例子你可能会认为不够
那么再次的假设是：1 2 3 4 5 6，6指向3，我们设置快指针是5，那么为什么上面是4，这里是5呢，这是为了保证在里面可以无限循环，比如5后面到6，那么他是慢慢加1的，而慢指针也是慢慢加1，所以是不会重合，即无限循环了，而其他的情况，必然会导致重合，只是时间问题而已，因为你始终接近慢的1，但是你可以发现，就算是设置5，那么一开始就是6，2，然后3，3，也重合的，所以我们才会说，可以随便移动快的指针，但是由于需要注意fast.next.next中next是否为null的情况，我们才只会操作设置为2的快指针（实际上因为对应的环对应设置，所以导致第二次移动时，必然会导致相等，所以这也是虽然可以移动的原因）

//这里我们就以快指向移动2，慢指针移动1开始操作
*/

代码如下，可以自己先看一遍，然后自行编写：

package test;

/**
 *
 */
public class test8 {

    //定义节点类
    public static class Node {
        int key;
        String name;
        Node next;

        public Node(int key, String name) {
            this.key = key;
            this.name = name;
        }
    }

    //我们直接定义方法：
    public static boolean isRing(Node head) {
        if (head == null) {
            System.out.println("没有头节点"); //进行提示，使得与环的问题相离
            return false; //如果对应没有节点，那么自然直接的返回false，
        }
        //定义初始的快慢指针
        Node slow = head; //慢指针
        Node fast = head.next; //快指针
        while (fast != null && fast.next != null) { //之所以将fast != null放在前面，是防止fast本身是null，导致fast.next报空指针异常，这是因为&&只要出现false，那么后续条件不会执行操作了
            //查看其当前或者他的下一个是否是null，如果是null，说明他是null或者下一个是null，那么就没有环了，因为已经到顶了

            //有环，顺便可以判断初始的指针
            if (slow == fast) {
                return true;
            }
            fast = fast.next.next;// 快指针步长为2
            slow = slow.next;//慢指针步长为1

        }
        return false;
    }

    public static void main(String[] args) {
        Node n1 = new Node(1, "张飞");
        Node n2 = new Node(2, "关羽");
        Node n3 = new Node(3, "赵云");
        Node n4 = new Node(4, "黄忠");
        Node n5 = new Node(5, "马超");
        n1.next = n2;
        n2.next = n3;
        n3.next = n4;
        n4.next = n5;
        n5.next = n1;
        System.out.println(isRing(n1));
    }


}

此种算法的时间复杂度为：O（n），因为他是循环链表的，但是可能快的指针能够更快的循环，所以可以认为是n/2-1次，忽略系数，认为是O（n）

0-1背包问题：

有n件物品和一个最大承重为W的背包，每件物品的重量是w[i]，价值是v[i]

在保证总重量不超过W的前提下，选择某些物品装入背包，背包的最大总价值是多少？

注意：每个物品只有一件，也就是每个物品只能选择0件或者1件

分析：

假设：W=10（背包重量），有5件物品，重量和价值如下：

w[1]=2，v[1]=6

w[2]=2，v[2]=3

w[3]=6，v[3]=5

w[4]=5，v[4]=4

w[5]=4，v[5]=6

我们一般在后面称为组合，比如w[1]=2，v[1]=6 就是（2，6）组合

由于只能选择1件物品，那么可以有如下：

dp数组的计算结果如下表：

i：选择的物品

j：最大承重

现在我们来解释一下上面的表：

首先是左边，左边是我们选择的物品，上边是最大承重，那么中间的值呢，他代表是该承重最大的价值是多少

从上到下的思考：

首先j是0和1，i是1，由于他们什么都不能选择，自然价值就是0

而j是2和3，i是1，由于他们选择的价值最大是（2，6）组合，所以都是6

那么4（4列那里，包括0的）为什么是中间的值从上到下是：6，9，9，9，9呢

我们第一个自然是分配一个（2，6）组合，而后面只能分配（2，3）组合了因为容量只有4

后面的就不多说，这里给出一个具体例子，即第9个重量，你可以发现中间的值从上到下是6，9，11，13，15，很明显，你可能不知道为什么，这里给出原因：

第一个是6，9-2=7，第二个是9，7-2=5，那么第三个怎么来的，因为由于5-6=-1，超过了重量，所以我们应该重新评估价格，这是因为在前面三个选择中，很明显（6，5）组合价值比（2，3）组合价值高（只能选取一个，且不考虑后续的情况下），所以直接省略了之前的操作，也就是7-2=5，变成7-6=1，总体由9（6+3）价值变成了11（6+5）个价值，然后继续往下，又可以发现，他的（5，4）组合可以结合（2，3）组合，所以又要进行重新判断，至此，你应该知道了上面的表代表什么意思了吧（即其第四个中的13就是6+3+4=13，同理6+3+6=15，因为他们相对的价值是最多的），他的意思也就是说，在考虑前面的物品的情况下的最好价值，比如如果是第4行，那么只考虑前4个物品，所以如果要实现前面的问题，我们只需要到第5行即可（0行忽略，即只考虑i=5的那一行数据），可以得出，即在重量为10的情况下，最好的价值就是15

你可能会有疑惑，单位价值中（2，3）组合必然是比（5，4）组合要好的，我可以将他们的单位价值来排序吗，答：不需要，因为我们是0-1问题，是不看单位价值的（即一个重量是多少价值），只看是否合适重量，才会考虑价值，且只能选择一个，比如我只剩下5个重量，因为只能选择一个（如果只考虑他们两个），那么我们必然是选择5 4，因为反正只能放入一个，即他们都合适重量（因为合适，所以不考虑单位重量），那么才会考虑价值，而4是大于3的，那么我们才会选择5 4

注意：上面只是逻辑的思考，并没有给出具体流程，只是让你知道为什么会是这样的值，而没有给通过流程来得到这样的值

解法：

dp方程：

/*
前面只是给出最好的价值出现的原因（逻辑思考的），那么在程序里面或者说有没有具体流程来使得得到最好的价值，即我们应该如何得到最好的价值呢，这是完成0-1背包的核心问题，只要解决了这一个问题，那么说明o-1背包问题解决，现在我们进行分析，由于我们是按照顺序来的，也就是先看前面的组合，然后看后面的组合，那么有以下的分析：
在保证前面的组合进行放入的情况下，再次考虑后续组合，这里最好理解，这是核心
也就是说，先判断当前所操作的行，然后来进行添加，如果我们的循环的重量，比如前面的j是1，i也是1，由于j是小于当前物品重量的，那么取前面一个值，即上一行（前面的所有物品）的值（也就是0，即价值），这是上面二维数组，为什么从1开始的主要原因，否则我们需要进行判断，使得如果是-1那么设置为0价值（后面会说明，即uu=0那里），那么需要格外的代码了，为什么取前面一个值的原因是：既然你的重量不满足，那么自然就是前面的是最好的值（因为保存的都是最好的）

如果循环的j是大于等于当前物品重量的，比如j是2，那么判断如下："当前上一行的该重量价值"与"当前物品价值+剩余重量在上一行中对应的价值"，谁大取哪个，这里就是核心的列子

既然我们知道了核心列子，我们主要分析这个："当前上一行的该重量价值"与"当前物品价值+剩余重量在上一行中对应的价值"，为什么要这样的设置，看如下解释：
先说明他的公式（式子或者方程）是否正确：
假设i是2，j是3，首先当前上一行的价值是6，但正是因为我们可以进行放入该物品
所以我们需要考虑总体（就如前面的由9变成11的一样）：当前物品（行）的价值是3，我们还剩余1个重量（因为3-2=1，注意：这个2是当前物品的重量），那么我们将这个剩余的重量进行查找，也就是从上一行找，因为上一行自然是其最好的价值，即我们找到上一行的第j是1的哪个值进行相加，很明显，他是0，所以当前上一行的价值是6，而当前物品价值加上上一行中剩余重量的最好值是3+0=3，那么取6，这里你可以发现，他的逻辑问题就是，如果满足当前的，那么剩余的重量取上一行的对应重量值，你可能还是有疑惑，为什么这样就能得出最好的结果呢（后面会进行说明的），那好，现在我们可以继续分析之前的第9个重量，即中间价值从上到下中的6 9 11 13 15中的11这个地方，使用具体流程来进行操作11
即主要参考其i是3，j是9的地方，我们可以发现，当前价值是5，9-6=3，还剩余3这个重量，那么我们来看看上一行中，3重量的最好价值，那么很明显就是6，所以他的结果就是11，因为当前上一行是9，11大于9，所以取11（当然，如果他们是相同的，那么自然取前者，在后面我们会使用Math.max，他的底层就是(a >= b) ? a : b;，即取前者）
至此，你可以发现，按照我们的逻辑是：如果有剩余重量，就比较当前上一行该重量的价值，与当前物品价值+上一行中剩余重量的对应的价值谁大，我们取大的，通过上面，可以发现，他的确能够解决最大的问题，可是你的疑惑可能还有，你可能认为上面不就是将公式进行运用吗，但没有说明为什么这样设置的原因，实际上上面的说明只是开始，即是让你知道他是可以作用的，即上面是前戏，现在才是重头戏：
我们知道按照前面的思考逻辑，我们在那里说明是通过重新判断来进行取得最大的值，但那里只是逻辑思考，没有具体流程而言，那么我们换一种思路，前面的说明是从上到下，那么我们现在从下到上：
假设他先取得当前所指向的物品，以i是1，j是2为例，那么j直到10都是6价值，当i是2时，j从2到10，在j是4时变成了9，我们先拿取当前的物品，然后拿取上一个的物品（从小到上），那么的确是9，注意：前面很明显的说明了，对应的j重量时，必然是最好的物品，因为都是从最好的情况来进行分析的，那么当i是3时，j从2到10，在j是8时变成了11，我们先拿取当前的物品，然后拿取上一个物品，当前的物品是（6，5）组合，接下来就是关键，因为我们是先拿当前物品，那么剩余的重量自然在上一行中就是其对应的最好物品，所以也就是3这个重量在上一行中是最好的物品，那么就是6的价值，即5+6=11，所以也就是说，满足自己，然后取剩余重量的最好情况
但是还有另外一种可能：如果当前物品价值加上剩余的价值，可能少于上一个，那么我们就要取上一个对应重量的价值
这里也有个问题，如果本身的重量大于其j重量，那么直接的取上一行重量对应的价值即可，否则看看上一行重量对应的价值与当前物品价值+剩余重量在上一行中对应的价值进行比较了，那么这里给出一个特殊情况，假设组合是：
（2，99）
（2，88）
（4，5）
当先到（4，5），你可能会认为由于先加上（4，5）可能结果不对了，那这是错误的，因为还有上一行重量对应的价值我们会比较了，所以说，实际上当前物品价值+剩余重量在上一行中对应的价值就是为了考虑当前物品加上与之前的区别，之前的是没有加上了，而这里是加上的，所以"当前上一行的该重量价值"与"当前物品价值+剩余重量在上一行中对应的价值"用你能够理解的话语就是："不考虑当前的物品"与"考虑当前的物品"的价值比较，由于保存的都是最好的，所有他们的重量操作是没有错误的，至此，说明完毕

这里我们假设定义一个数组，也就是上面图片中的数组，很明显，我们需要二维数组，因为0的存在，所以我们可以定义如下：
int[][]dp=new int[values.length+1][max+1];，其中values.length是5，也就是左边的价值，max也就是最大重量
那么物品重量呢，我们使用int[] weights来表示对应价值的对应重量，因为我们会设置int[] weights与int[] values是对应的，所以通过相同下标可以找到对应的价值和重量

那么我们应该循环上面的图片二维数组的次数，也就是：
for(int i=1;i<=values.length;i++){
            for(int j=1;j<=max;j++){
从1开始，因为0不用考虑，但是他还需要用处，后面你就知道了（因为从1开始，所以对应的weights下标需要减1）：

现在我们选择一个物品，首先判断他是否大于总重量（背包）

如果w[i-1] >j，即若当前物品重量大于背包重量，那么直接取上一行该重量的值，也就是dp(i,j)=dp(i-1,j)，因为0的存在，所以可以发现，0在这里是非常好的，即可以用来作为初始数据
而w[i-1]<=w，即若当前物品重量小于背包重量，那么我们就会考虑选择他，这时因为=的存在，所以会用到左边的0，那么0在这里也是非常好的


至此，上面大致说明完毕，现在，我们来进行编写：

*/

可以自己看一遍，然后自行编写：

package test;

/**
 *
 */
public class test9 {
    //参数1：物品价值，参数2：物品重量，参数3：背包重量，用来设置dp数组的j的最大值
    public static int maxValue(int[] values, int[] weights, int max) {
        if (values == null || values.length == 0) return 0;
        if (weights == null || weights.length == 0) return 0;
        if (values.length != weights.length || max <= 0) return 0; //需要进行对应，否则直接返回，因为总不能一个物品对应两个重量或者两个价值吧，所以这里需要是长度相同的才可往下操作
        //如果对应的数组是空的，或者背包是没有重量的，那么返回0，即什么都没有拿取

        //dp数组
        int[][] dp = new int[values.length + 1][max + 1]; //设置数组，我们以max为基准
        //从1开始
        for (int i = 1; i <= values.length; i++) {
            for (int j = 1; j <= max; j++) {
                //选择的物品超过最大承重
                if (j < weights[i - 1]) {
                    //最大价值=上一轮的最大价值（不选择当前物品，因为重量不够）
                    dp[i][j] = dp[i - 1][j];
                }
                //否则可选择该物品
                else {
                    //上一轮的最大价值（不选择该物品）与选择该物品进行比较，我们取两者的最大值
                    dp[i][j] = Math.max((dp[i - 1][j]), values[i - 1] + dp[i - 1][j - weights[i - 1]]);

                }
            }
        }
        return dp[values.length][max]; //返回最后一行，然后是max的重量即可
    }

    public static void main(String[] args) {
        int[] values = {6, 3, 5, 4, 6};
        int[] weights = {2, 2, 6, 5, 4};
        int max = 10;
        System.out.println(maxValue(values, weights, max));
    }

}

//如果你的循环非要从0开始，并且数组去除两边的0，那么可以操作如下代码：
package test;

/**
 *
 */
public class test9 {
    public static int maxValue(int[] values, int[] weights, int max) {
        if (values == null || values.length == 0) return 0;
        if (weights == null || weights.length == 0) return 0;
        if (values.length != weights.length || max <= 0)
            return 0;

        int[][] dp = new int[values.length][max]; //从0开始，去除了两边的0，即不用加1了
        for (int i = 0; i < values.length; i++) {
            for (int j = 0; j < max; j++) {
                if (j + 1 < weights[i]) { //需要从1开始，使得与前面去掉的一样，因为前面也是没有操作0的位置
                    int l = 0;
                    if (i != 0) {
                        l = dp[i - 1][j];
                    }
                    dp[i][j] = l;
                } else {
                    int ii = 0;
                    int oo = 0;
                    if (i != 0) {
                        ii = dp[i - 1][j];
                        int uu = j - weights[i]; //因为j+1，所以需要考虑下标越界，但由于去掉了对应的0，所以-1和0是相同的结果（因为-1和0就是原来的0，1的结果，都是0价值结果的意思），即uu设置为0，使得是相同的结果（即都是0价值的结果）
                        if (uu < 0) {
                            uu = 0;
                        }

                        oo = dp[i - 1][uu];
                    }
                    dp[i][j] = Math.max(ii, values[i] + oo);

                }
            }
        }
        return dp[values.length - 1][max - 1];
    }

    public static void main(String[] args) {
        int[] values = {6, 3, 5, 4, 6};
        int[] weights = {2, 2, 6, 5, 4};
        int max = 10;
        System.out.println(maxValue(values, weights, max));
    }

}

时间复杂度为： O（i*j），i代表物品数量，j代表背包重量

可以看出动态规划是计算的值是上次的某个值+这次的值，是一种用空间换时间的算法

至此，我们的数据结构和算法大致说明完毕（选取主要的来进行学习，就比如二叉树那里有很多种数据结构的类型，但我们只是说明主要的情况或者类型）