一、卷积定义
卷积计算过程如图1所示,即输入矩阵和核函数对应的位置相乘,然后相加得到输出对应位置的数。

图1. 卷积计算过程
该过程可以形象地从图2中展现。
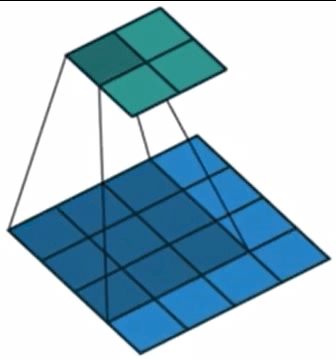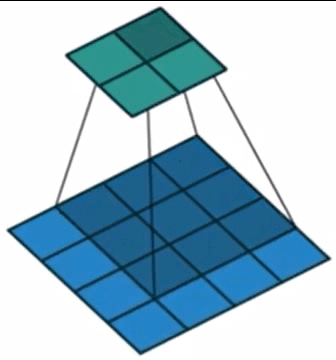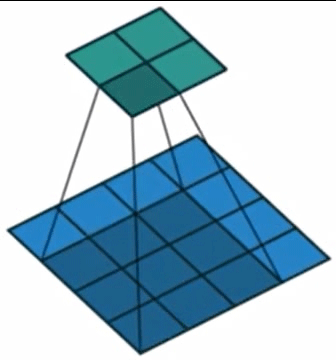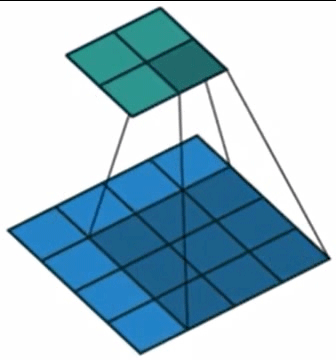
图2. 二维卷积示意图
二、代码实现
2.1 实现互相关运算
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): #@save
"""计算二维互相关运算"""
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Yh,w为卷积核的行、列数
Y为输出矩阵,它的行、列数为X.shape[0] - h + 1和 X.shape[1] - w + 1,X.shape[0] 为输入矩阵的行数,X.shape[0] - h 为卷积核可以向右移动的步数,因为移动步数为零时也会计算出一个值,所以 X.shape[0] - h + 1 为输出结果的行数,列数同理。
X[i:i + h, j:j + w] * K 表示从输入矩阵中提取一个子矩阵,索引范围为,即包含左边不包含右边,乘法表示对应元素相乘。
2.2 训练卷积网络的简单实现
import torch
from torch import nn
from d2l import torch as d2l
X = torch.ones((6, 8))
X[:, 2:6] = 0
Y = torch.zeros((6, 7))
# 构造一个二维卷积层,它具有1个输出通道和形状为(1,2)的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)
# 这个二维卷积层使用四维输入和输出格式(批量大小、通道、高度、宽度),
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2 # 学习率
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat - Y) ** 2
conv2d.zero_grad()
l.sum().backward()
# 迭代卷积核
conv2d.weight.data[:] -= lr * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f'epoch {i+1}, loss {l.sum():.3f}')三、填充与步幅
填充(padding)指在输入矩阵周围添加行列,使卷积后得到的结果行列数更多。效果如图3所示。
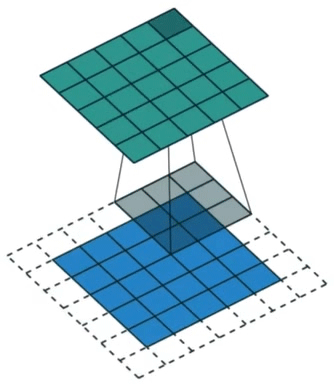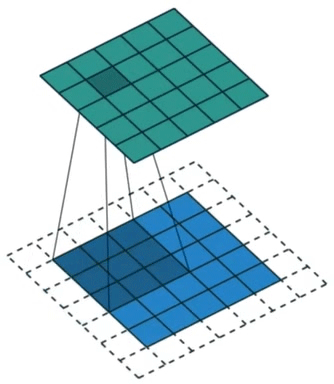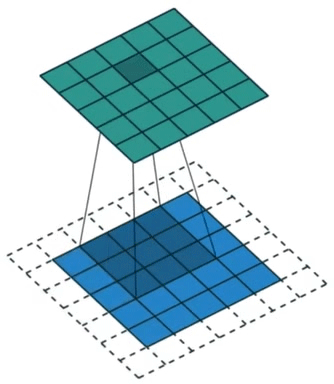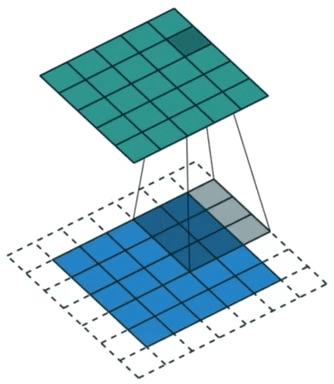
图3. 卷积填充示意图
import torch
from torch import nn
# 为了方便起见,我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重,并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
# 这里的(1,1)表示批量大小和通道数都是1
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
# 省略前两个维度:批量大小和通道
return Y.reshape(Y.shape[2:])
# 请注意,这里每边都填充了1行或1列,因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape
# 上下各填充2行,左右各填充1列,总计填充4行2列
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape步幅(stride)指卷积核每次移动距离,增加步幅可以在不增加卷积核尺寸的条件下使得到的结果行列数更少。效果如图4所示。
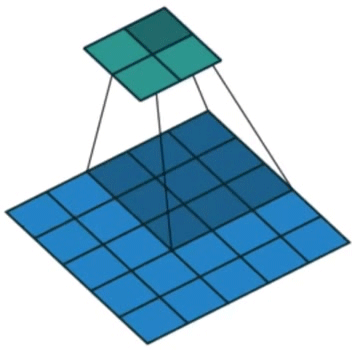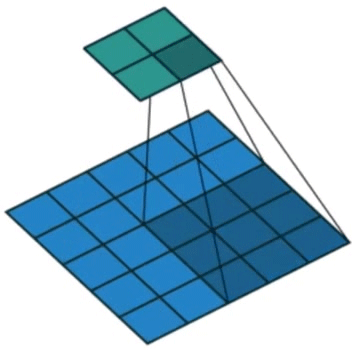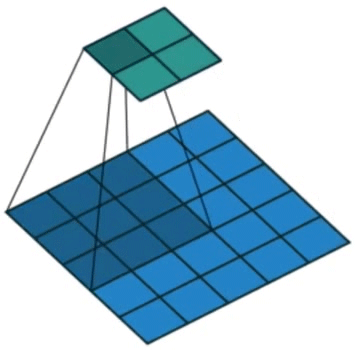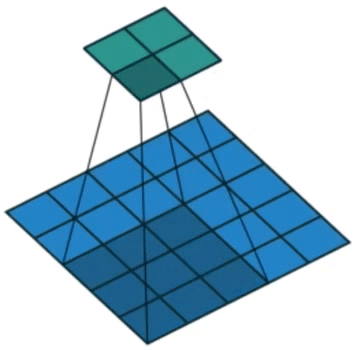
图4. 卷积步幅示意图
import torch
from torch import nn
# 向右移动的步幅与向下移动的步幅均为2
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
X = torch.rand(size=(8, 8))
print(comp_conv2d(conv2d, X).shape) # 输出 torch.Size([4, 4])
X = torch.rand(size=(8, 8))
# padding之后,size=(8,10),输出行数=1+(8-3)/3=2,输出列数=1+(10-5)/4=2
# 行向移动的stride=3,列向移动的stride=4
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
print(comp_conv2d(conv2d, X).shape) # 输出 torch.Size([2, 2])