特征提取与匹配

路标是三维空间中固定不变的点，可以在特定位姿下观测到
在视觉SLAM中，可利用图像特征点作为SLAM中的路标

特征点

特征点是图像中最具代表性的部分，如轮廓、边缘、最暗或最亮的部分

特征点具有以下性质
在这里插入图片描述
特征点的信息：

关键点：位置、大小、方向、评分等
描述子：特征点周围的图像信息

ORB特征

ORB特征的关键点是：Oriented FAST（一种改进的FAST角点）
描述子：改进BRIEF
FAST关键点：
FAST：主要检测局部像素灰度变化明显的地方，（如果一个像素与邻域的像素差别较大，则更可能是角点），检测过程如下：
在这里插入图片描述

在这里插入图片描述
在FAST12中，提出一个高效的测试，来快速排除一大部分非特征点的点，该测试仅仅检查位置1、5、9、13四个位置的像素，如果不满足至少三个角点亮度大于I+T或小于I-T，那么p不可能是一个角点。
FAST缺点：

原始FAST角点经常出现扎堆的现象。所以在第一遍检测之后，还需要用非极大抑制，在一定区域内仅保留响应极大值的角点，避免角点集中问题。
由于FAST角点不具有方向信息且存在尺度问题，ORB添加了尺度和旋转的描述：尺度不变性通过构建图像金字塔来实现，旋转是由灰度质心法来实现的。
Oriented FAST:
👉尺度不变性

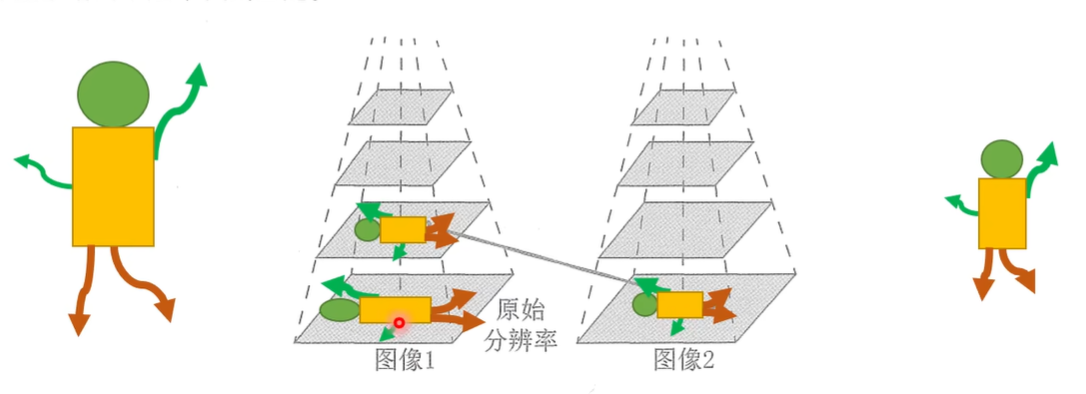
很好的避免了尺度不变性
👉旋转是由灰度质心实现的
质心是指以图像块灰度值作为权重的中心。
在这里插入图片描述

描述子：
一种二进制描述子，其描述向量由许多01组成

1：关键点附近两个像素p>q
0: 关键点附近两个像素p<q

在这里插入图片描述

example:

那么怎么旋转的呢？

BRIEF描述子总结

优点：使用了随机选点的比较，速度标记快，由于使用二进制表达，存储起来十分方便
缺点：原始的BRIEF描述子具有旋转不变性，在图像发生旋转时容易丢失，而ORB在FAST特征提取阶段计算了关键点的方向，计算了旋转之后的BRIEF特征使ORB的描述子具有较好的旋转不变性。
BRIEF是一种二进制描述，需要用汉明距离度量（即其中01个数的差异）

特征匹配

特征匹配解决了SLAM中的数据关联问题，即确定当前看到的路标与之前看到的路标之间的对应关系。
通过对图像或者图像与地图之间的描述子进行准确匹配，可以为后续的姿态估计、优化等操作减轻大量负担，然而，由于图像特征的局部特征、误匹配的情况存在。
对于两个时刻的图像：

在图像It中提取到特征点xm(m=1,2…M)在图像It+1时刻提取到特征点xn(n=1,2…N)
暴力匹配：对于每一个特征点xm与所有xn测量描述子的距离，然后排序，取最近的一个作为匹配点
当特征点数量很大时，匹配的运算量会变得很大，选用一些改进算法：快速近似最近邻算法

计算相机运动

2D-2D对极集合

在这里插入图片描述

)
需要用到相机坐标系->像素坐标系相关知识

👉 对极几何

在这里插入图片描述
本质矩阵仅依赖于外部参数R,t
👉八点法求E
将E看作3*3的矩阵，去掉尺度因子后剩下8个自由度，考虑一对匹配点，其归一化坐标为:

把上述方程记为
Ae=0
如果给定的匹配点多于8，该方程构成一个超定方程，即不一定存在e使得上式成立，此时可以计算一个最小二乘解
在这里插入图片描述
求出了在最小二乘意义下的E矩阵。

（超定方程是指具有多于未知数的方程组。在超定方程中，未知数的个数大于等于方程的个数。这种情况下，通常不存在一个恰好满足所有方程的解。因此，超定方程往往没有唯一解，而是寻求最小二乘解或最优解。最小二乘解是使得所有方程误差的平方和最小化的解，而最优解则是根据给定的目标函数和约束条件来确定的最佳解）

在这里插入图片描述
👉从E中分解R和t
对E进行奇异值分解

（U与V是正交阵，）

奇异值分解（SVD）是一种矩阵分解的方法。对于一个m×n维的矩阵A，它可以表示为以下形式的矩阵乘积：

A = UΣV^T

其中，U是一个m×m维的正交矩阵，Σ是一个m×n维的对角矩阵，V是一个n×n维的正交矩阵的转置。

在Σ中，对角线上的元素称为奇异值，按照从大到小的顺序排列。而U和V中的列向量分别称为左奇异向量和右奇异向量，它们都是正交向量。

SVD可以将原始矩阵A分解成三个部分，U、Σ和V，这些部分包含了矩阵A的重要信息。

三角测量、PNP、ICP

3D-2D:PNP

已知：

1.3D：上一帧的相机坐标系下的3D点。
2.2D：两幅图片的匹配点信息，像素坐标。
3.其他：相机内参
> 求：两帧之间的变化矩阵R,t

👉直接线性变换（DLT）
在这里插入图片描述

👉P3P
输入数据为3对 3D-2D匹配点

P3P总结：
利用三角形相似性质，求解A,B,C在当前相机坐标系下的3D坐标，转换一个3D-3D的位姿估计问题=》ICP
❗❗❗👉非线性优化不太会
前面说的线性优化方法，往往是先求相机位姿，再求空间点位置，非线性优化则是把它们都看成优化变量，放在一起优化，因此可以构建一个定义于李代数上的非线性最小二乘问题。
分析目标函数：我们通过特征匹配知道p1,p2是同一空间点的投影，估计了一个相机位姿，使得3D的实际投影位置与观测位置存在一个误差（重投影误差），则把误差求和，构建最小二乘问题，然后寻找最好的相机位姿，使其最小化。
在这里插入图片描述