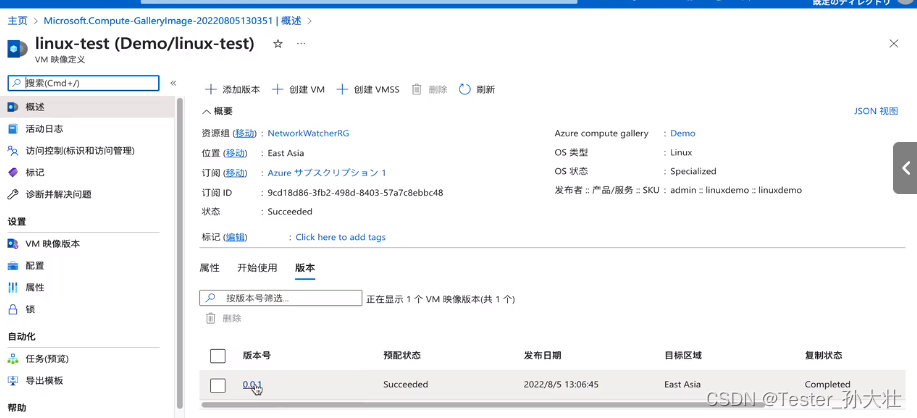
奇异值和特征值都描述了一个矩阵的一些特性，但很多情况下，对于两者之间的区别和联系都不太清楚。

本文就这两者进行解析，并对奇异值的一些简单应用进行探索。

奇异值与特征值的定义

奇异值与特征值都被用于描述矩阵作用于某些向量的标量，都是描述该向量模长变化幅度的数值。矩阵与向量的乘积得到一个新的向量，几何上相当于对向量进行了旋转和拉伸，就像是对向量施加了一个作用，或者说是变换。

定义：

• 如果有向量$v$能使得矩阵$A$与之的积$Av=\lambda v$，$\lambda$为标量，那么$\lambda$和$v$就分别是$A$的特征值与特征向量
• 如果存在单位正交矩阵$U$和$V$，使得$A=UD{V}^T$，$D$为对角矩阵，对角线上的值被称为奇异值，$U$和$V$中的列分别被称为$D$的左奇异向量和右奇异向量

特征值只能在方阵中进行，而奇异值则没有这个限制。

如果考虑矩阵的维度，奇异值的定义为：

对于一个秩为$r$的矩阵$A_{m\ast n}$，必存在$m\ast m$的正交矩阵$U_{m\ast m}$，$n\ast n$的正交矩阵$V_{n\ast n}$，$m\ast n$的矩阵$D_{m\ast n}$，使得：

$$A_{m\ast n}=U_{m\ast m}{D}_{m\ast n}{V}_{n\ast n}^T=U_{m\ast m}{\left[\begin{array}{cc}{\Sigma }_{r\ast r}& 0\\ 0& 0\end{array}\right]}_{m\ast n}{V}_{n\ast n}^T$$

特征值

从定义中可看出，特征向量给出了方向不变作用的方向。 当$A$作用于特征向量时（$Av$），它只是将特征向量$v$数乘一个标量（对应的特征值$\lambda$），相当于将$v$长度变化了$\lambda$倍，若$\lambda$为正，$v$方向保持不变；否则，$v$方向反转。

例如：对于矩阵$A=\left[\begin{array}{cc}1& \frac{1}{3}\\ \frac{1}{3}& 1\end{array}\right]$，单位圆被变换为椭圆，特征向量是所有向量中经过线性变换（乘以$A$）后，方向不变的向量。

奇异值

特征向量不变的方向并不保证是拉伸效果最大的方向，而这是奇异向量的方向。

奇异值是非负实数，通常从大到小顺序排列。

${\sigma }_1$是矩阵$A$的最大奇异值，对应右奇异向量$v$。$v$是$arg{\max }_{x,|x|=1}(||Ax|{|}_2^2)$的解，换句话说：在$A$与所有单位向量$x$的乘积中，$||Av|{|}_2^2={\sigma }_1$是最大的；但不保证乘积后方向不变。

怎么理解这一点呢？

对于$A=UD{V}^T$，可以这么理解：

• $V^T$：旋转（正定矩阵）
• $D$：缩放或拉伸（对角矩阵）
• $U$：旋转（正定矩阵）

由于SVD分解对于$A$本身没有任何的限制，也就是说，任何矩阵变换总可以看成旋转+缩放或拉伸+旋转的过程。

既然这样，那么对于拉伸效果最大的判断，就是看$D$矩阵中最大的奇异值了。

例如：对于矩阵$A=\left[\begin{array}{cc}1& \frac{1}{3}\\ \frac{1}{3}& 1\end{array}\right]$，单位圆被变换为椭圆，奇异向量对应椭圆的半长轴，不同于上例中同一矩阵的特征值方向。

区别与联系

从上面的图中可以清楚的看到，奇异值与特征值的差异在于：

• 特征向量描述的是矩阵的方向不变作用的向量
• 奇异向量描述的是矩阵最大作用的方向向量

而它们的关联在于：

• $A^{T}A$和$A{A}^T$特征值是$A$的奇异值的平方（具体的解释分析见下文）

方向不变和拉伸最大都是矩阵内禀的性质，方向不变在马尔可夫随机场中非常重要；而拉伸最大的方向则是数据方差分布最大的方向，所含信息量最大，是PCA等方法中的核心思想。

$A$的奇异值与$A^{T}A$和$A{A}^T$的特征值的关系

首先，我们需要简单回顾一下特征值与特征向量：

如果对于任意方阵A，假设求得$n$个特征值$[{\lambda }_1,{\lambda }_2,...,{\lambda }_n]$，对应到特征向量为$[x_1,x_2,...x_n]$，其中每一个$x_i$均为一个列向量。我们分别构建特征值对应的对角阵$\Sigma$和特征向量构建的矩阵$W$，有：

$$\Sigma =\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]$$

$$W=\left[\begin{array}{cccc}{x}_1& x_2& ...& x_n\end{array}\right]$$

那么结合$Ax=\lambda x$，我们得到如下等式，即$A$的特征分解表达式：

$$AW=W\Sigma \Rightarrow A=W\Sigma W^{-1}$$

进一步，由于特征向量是原空间经过线性变换后的方向向量，因此我们可以对每个特征向量进行尺度缩放，令其模长为1（归一化），即$||x_i|{|}_2^2=1$。那么此时构建的$n$个特征向量组成的矩阵$W$则为正交矩阵，即满足$W^T=W^{-1}$。因此，$A$的特征分解表达式可改写为：

$$A=W\Sigma W^T$$

有了以上结论，我们就可以进一步去探寻$A^{T}A$的特征值与$A$的奇异值之间的关系了。

我们知道，$A$的SVD分解结果为：

$$A=UD{V}^T=U\left[\begin{array}{c}\Sigma \\ 0\end{array}\right]V^T$$

因此：

$$A^T=V{D}^T{U}^T=V\left[\begin{array}{cc}\Sigma & 0\end{array}\right]U^T$$

那么有：

$$A^{T}A=V{D}^T{U}^{T}UD{V}^T$$

由于$U$是正交矩阵：

$$A^{T}A=V{D}^{T}D{V}^T=V{\Sigma }^2{V}^T$$

因此我们发现对$A$的右奇异矩阵$V$正好是$A^{T}A$的特征向量构建的矩阵$W$。同时，$A^{T}A$特征值是$A$奇异值的平方。

同理：

$$A{A}^T=UD{V}^{T}V{D}^T{U}^T=UD{D}^T{U}^T=U{\Sigma }^2{U}^T$$

因此我们发现对$A$的左奇异矩阵$U$正好是$A{A}^T$的特征向量构建的矩阵$W$。同时，$A{A}^T$特征值是$A$奇异值的平方。

在文章【Math】线性方程组的最小二乘解中，对齐次方程组的最小二乘解进行分析，其中对应的特征值解和奇异值解。根据结论，特征值解为$A^{T}A$最小特征值对应的特征向量，奇异值解为$A$最小奇异值对应的右奇异向量。

根据本文结论，$A^{T}A$特征值是$A$奇异值的平方，因此最小奇异值就对应着最小特征值，又因为$A$的右奇异矩阵$V$矩阵正好是$A^{T}A$的特征向量构建的矩阵$W$，因此$A^{T}A$最小特征值对应的特征向量等同于$A$最小奇异值对应的右奇异向量。这并不矛盾。

对于SVD分解与特征值特征向量的关系，我们还应该想到，$A$的SVD分解结果亦可通过特征分解得到。其中求解$A^{T}A$的特征向量对应SVD中的$V$；求解$A{A}^T$的特征向量对应SVD中的$U$；而$D$也可通过特征值求平方根得到；最后在构建$UD{V}^T$各矩阵行列顺序的时候，按照奇异值$\sigma$从大到小的顺序构建即可。

奇异值分解的求法

根据$A$的奇异值与$A^{T}A$和$A{A}^T$的特征值的关系，我们就可以通过特征值的求法，来进行奇异值分解，下面介绍一下步骤：

第一步：求出$A_{m\ast n}^T{A}_{m\ast n}$的$n$个特征值${\lambda }_1$、${\lambda }_2$、$...$、${\lambda }_r$、${\lambda }_{r+1}=0$、${\lambda }_{r+2}=0$、$...$、${\lambda }_n=0$（并按照从大到小排列）和对应的标准正交的特征向量$v_1$、$v_2$、$...$、$v_r$、$v_{r+1}$、$v_{r+2}$、$...$、$v_n$

第二步：取标准正交的特征向量构成正交矩阵

$$V_{n\ast n}={\left[\begin{array}{cccccccc}{v}_1& v_2& ...& v_r& v_{r+1}& v_{r+2}& ...& v_n\end{array}\right]}_{n\ast n}$$

取正奇异值，即前$r$个奇异值，即非零特征值开根号$\sqrt{{\lambda }_1}$、$\sqrt{{\lambda }_2}$、$...$、$\sqrt{{\lambda }_r}$，构成对角矩阵

$${\Sigma }_{r\ast r}={\left[\begin{array}{cccc}\sqrt{{\lambda }_1}& & & \\ & \sqrt{{\lambda }_2}& & \\ & & \ddots & \\ & & & \sqrt{{\lambda }_n}\end{array}\right]}_{r\ast r}$$

添加额外的$0$组成$m\ast n$的矩阵：

$$D_{m\ast n}={\left[\begin{array}{cc}{\Sigma }_{r\ast r}& 0\\ 0& 0\end{array}\right]}_{m\ast n}$$

第三步：求出$A_{m\ast n}{A}_{m\ast n}^T$的$m$个特征值${\lambda }_1$、${\lambda }_2$、$...$、${\lambda }_r$、${\lambda }_{r+1}=0$、${\lambda }_{r+2}=0$、$...$、${\lambda }_m=0$（并按照从大到小排列）和对应的标准正交的特征向量$u_1$、$u_2$、$...$、$u_r$、$u_{r+1}$、$u_{r+2}$、$...$、$u_n$

第四步：取标准正交的特征向量构成正交矩阵

$$U_{m\ast m}={\left[\begin{array}{cccccccc}{u}_1& u_2& ...& u_r& v_{r+1}& u_{r+2}& ...& u_m\end{array}\right]}_{m\ast m}$$

结束。

再思考一下，因为$A^{T}A$和$A{A}^T$的秩相等、特征值一致，感觉第三步第四步有点重复的意思了，还有没有其他的办法代替这两步么？

从另个角度看：

$$A=UD{V}^T\Rightarrow AV=UD{V}^{T}V$$

由于$V$是正交矩阵，可以得到：

$$AV=UD\Rightarrow A{v}_i={\sigma }_i{u}_i\Rightarrow u_i=\frac{1}{{\sigma }_i}A{v}_i$$

这个时候，可以看到$\Sigma$的维度为$r$，$V$的维度为$n$，最多只可以计算出$U$的$r$个维度，还缺$m-r$个维度。此时可以通过标准正交的基扩充方法，将$u_1$、$u_2$、$...$、$u_r$扩充为$m$维向量空间的标准正交基$u_1$、$u_2$、$...$、$u_r$、$b_1$、$b_2$、$...$、$b_{m-r}$，组成正交矩阵：

$$U_{m\ast m}={\left[\begin{array}{cccccccc}{u}_1& u_2& ...& u_r& b_1& b_2& ...& b_{m-r}\end{array}\right]}_{m\ast m}$$

关于标准正交的基扩充，可以参考文章：奇异值分解（SVD）的定义、证明、求法。

奇异值的应用

假设想要对图片进行压缩，图片的像素矩阵为$A_{m\ast n}$。根据SVD分解，可以将$A_{m\ast n}$进行转换为：

$$A_{m\ast n}=U_{m\ast m}{D}_{m\ast n}{V}_{n\ast n}^T$$

我们现在存储的是$U_{m\ast m}$、$D_{m\ast n}$、$V_{n\ast n}$三个矩阵。如何能够压缩这$3$个矩阵的维度呢？

对于$m$行$n$列的矩阵$A$, 通过SVD分解之后，拆分成了$3$个子矩阵，其中$U$矩阵为$m$行$n$列的方阵，$V$矩阵为$n$行$n$列的方阵，$D$矩阵为只有对角线有值的矩阵，其中的值称之为奇异值。

在奇异值分解中，$D$矩阵的奇异值是按照从大到小的顺序排列的，而且减少的特别快，经常前$10\%$的奇异值就占据了全部奇异值$99\%$以上的比例。基于这个性质，我们可以只提取前几个奇异值及其对应的矩阵来近似的描述原来的矩阵。

通常，$D$矩阵可以根据$A$矩阵的秩$r$进行划分块：

$$D_{m\ast n}={\left[\begin{array}{cc}{\Sigma }_{r\ast r}& 0\\ 0& 0\end{array}\right]}_{m\ast n}$$

如果只取前$k$个奇异值，且$k\ge r$，那么新的矩阵较原来的矩阵是无损的。这是因为，$\Sigma$矩阵的奇异值表示其对应的特征，而当$k\ge r$时，$D_{k\ast k}$已经包含了${\Sigma }_{r\ast r}$的所有非零元素，所以其是可以完美复原出来的。

例如：

$$A_{4\ast 5}=\left[\begin{array}{ccccc}1& 0& 0& 0& 2\\ 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{array}\right]$$

可以SVD分解为：

$$A_{4\ast 5}=U_{4\ast 4}{D}_{4\ast 5}{V}_{5\ast 5}^T=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\end{array}\right]\left[\begin{array}{ccccc}4& 0& 0& 0& 0\\ 0& 3& 0& 0& 0\\ 0& 0& \sqrt{5}& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ \sqrt{0.2}& 0& 0& 0& \sqrt{0.8}\\ 0& 0& 0& 1& 0\\ \sqrt{0.8}& 0& 0& 0& -\sqrt{0.2}\end{array}\right]$$

如果$U$取前$3$列，$D$取前$3$行$3$列，$V^T$取前$3$行，那么：

$$U_{4\ast 3}{D}_{3\ast 3}{V}_{3\ast 5}^T=\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 0& 0& 0\\ 1& 0& 0\end{array}\right]\left[\begin{array}{ccc}4& 0& 0\\ 0& 3& 0\\ 0& 0& \sqrt{5}\end{array}\right]\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ \sqrt{0.2}& 0& 0& 0& \sqrt{0.8}\end{array}\right]=\left[\begin{array}{ccccc}1& 0& 0& 0& 2\\ 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{array}\right]$$

可以看到，该值与$A_{4\ast 5}$完全一致。

如果$U$取前$2$列，$D$取前$2$行$2$列，$V^T$取前$2$行，那么：

$$U_{4\ast 2}{D}_{2\ast 2}{V}_{2\ast 5}^T=\left[\begin{array}{cc}0& 0\\ 0& 1\\ 0& 0\\ 1& 0\end{array}\right]\left[\begin{array}{cc}4& 0\\ 0& 3\end{array}\right]\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\end{array}\right]=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{array}\right]$$

此时看到，该值与$A_{4\ast 5}$不一致。

因此，假设$A$的秩为$r$，有：

$$A_{m\ast n}=U_{m\ast m}{D}_{m\ast n}{V}_{n\ast n}^T\approx U_{m\ast k}{D}_{k\ast k}{V}_{k\ast n}^T$$

• 当$k\ge r$时，没有损失
• 当$k<r$时，$k$越大，损失的越小

图片压损也就是采用这个原理，可以将图片的矩阵进行SVD分解，取其前$k$个奇异值，然后重新计算出该图片的样式。

PCA主成分分析法，其实也是采取的同样近似的原理，所谓主成分，就是奇异值较大的几个子矩阵，用它们来代替整体的矩阵。

相关阅读

• 白话来说SVD奇异值分解(1)→原理推导与奇异值求解举例
• 奇异值与特征值辨析
• 奇异值分解
• 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用