目录

题目：

示例：

分析：

代码：

---

题目：

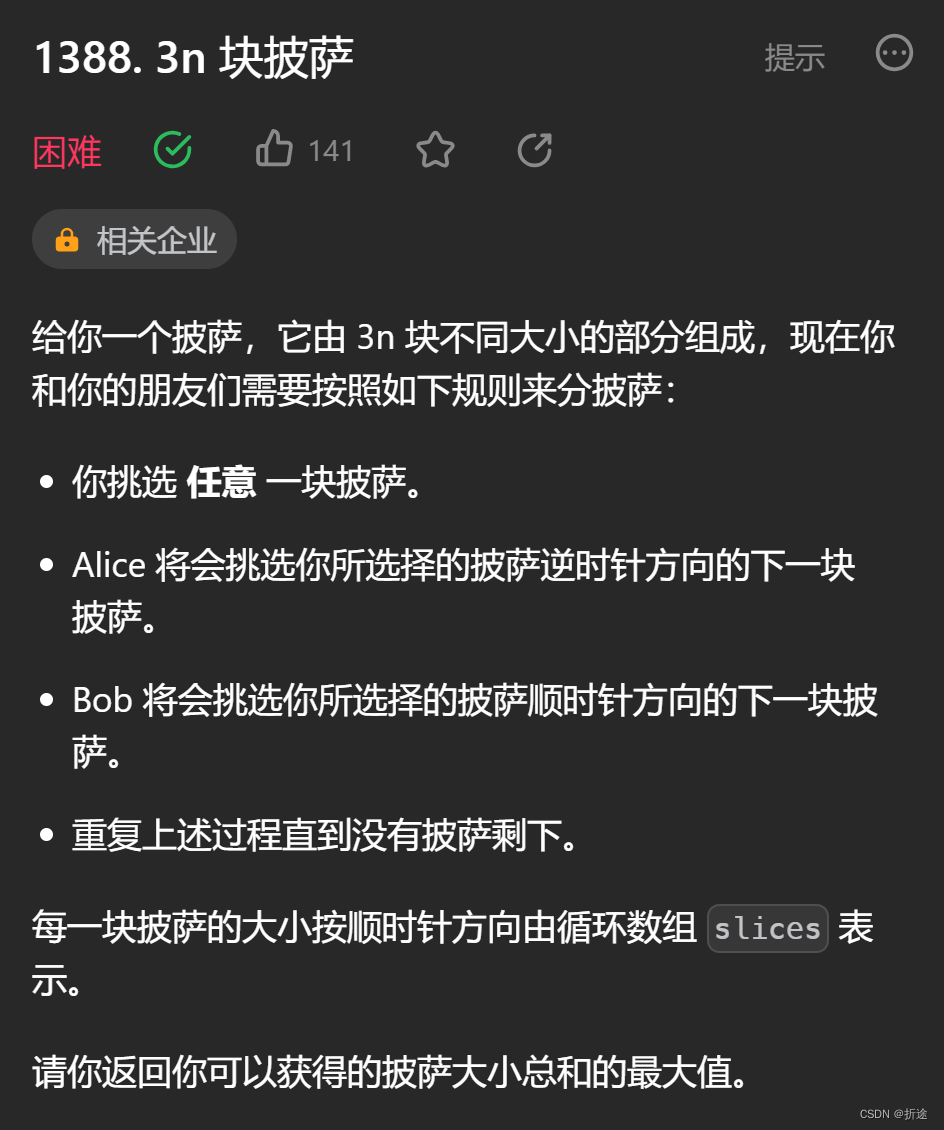
示例：

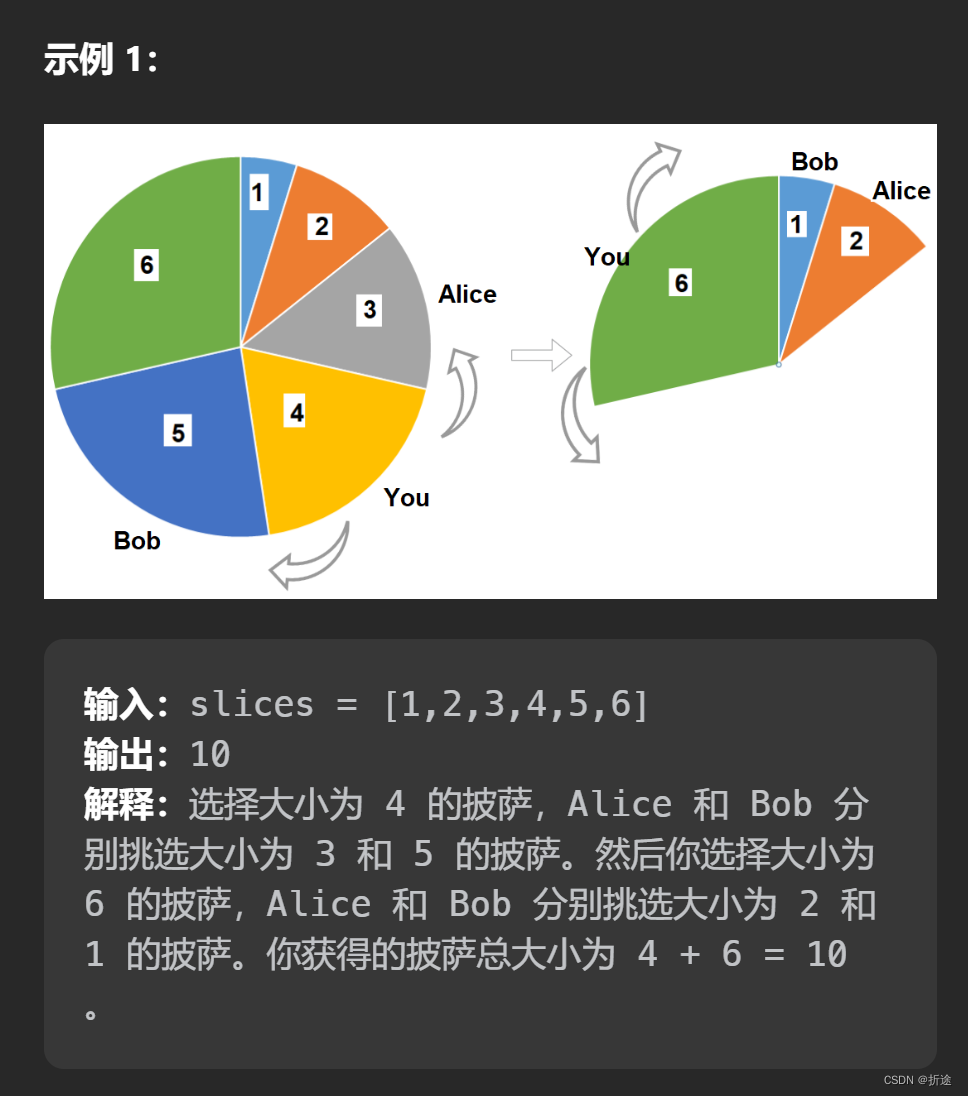
分析：

题目给我们一个披萨，分成了3n块，每次我们可以选择一块，而我们的两个小伙伴会拿走我们选的披萨的相邻的两块。

我们可以把披萨的模型转变为数组，只不过这个数组是首尾相连的：

 那么问题就变成了我们不能选择相邻的披萨，问我们可以获取的最大的披萨是多少。

这和打家劫舍2有异曲同工之妙，都是不能取相邻的两个数，并且数组也是首尾相连的：

 和打家劫舍2不同的是，本题中我们是固定取走n块披萨的，而打家劫舍2中没有明确说明偷几家。

因此本题的dp数组是二维的，dp[ i ][ j ]的含义我们定义为有 i 块披萨的情况下，我们已经获取了 j 块披萨，此时获取的最大的值。

所以我们的递推公式可以是：

dp[i][j]=max(slices[i]+dp[i-2][j-1],dp[i-1][j]);

意思是有i块披萨并且取j块披萨的情况下能获取的最大值为取本块披萨的值加上有 i - 2 块披萨并且取了 j - 1 块披萨的最大值以及不取本块披萨保持有 i - 1 块披萨且取了 j 块披萨的状态的二者的最大值。

我们再来处理一下数组首尾相连的问题，实际上数组首尾相连对我们有影响的是，不能同时取第一个元素和最后一个元素，因此我们的处理办法可以借鉴一下打家劫舍2，我们分两次动态规划，一次是假设我们没有第一块披萨然后动态规划，第二次是假设我们没有最后一块披萨然后动态规划。最后把两次的结果取一个最大值即可。

这样就不会同时取到了第一块披萨和最后一块披萨，也就满足了首尾相邻数组的限制了。

代码：

class Solution {
public:
    int maxSizeSlices(vector<int>& slices) {
        int n=slices.size();
        //dp[i][j]为有i块披萨的情况下,选择了j块披萨时能获取到的最多的数
        vector<vector<int>>dp(n,vector<int>(n/3+1,0));
        dp[0][1]=slices[0];
        dp[1][1]=max(slices[0],slices[1]);
        for(int i=2;i<n-1;i++){ //不取最后一块,所以可以不用遍历n-1
            for(int j=1;j<=n/3;j++){
                //有i块披萨并且取j块披萨的情况下能获取的最大值为
                //max(取本块披萨+有i-2块披萨并且取了j-1块披萨的最大值,
                //不取本块披萨保持有i-1块披萨且取了j块披萨的状态)
                dp[i][j]=max(slices[i]+dp[i-2][j-1],dp[i-1][j]);
            }
        }
        int res=dp[n-2][n/3];   //取第一块披萨不取最后一块披萨的情况
        dp=vector(n,vector<int>(n/3+1,0));
        dp[1][1]=slices[1];
        dp[2][1]=max(slices[1],slices[2]);
        for(int i=3;i<n;i++){
            for(int j=1;j<=n/3;j++){
                dp[i][j]=max(slices[i]+dp[i-2][j-1],dp[i-1][j]);
            }
        }
        res=max(res,dp[n-1][n/3]);  //取最后一块披萨不取第一块披萨的情况
        return res;
    }
};