目录
- 二进制介绍
- 二进制
- 2进制转10进制
- 10进制转2进制数字
- 2进制转8进制和16进制
- 2进制转8进制
- 2进制转16进制
- 原码、反码、补码
- 移位操作符
- 左移操作符
- 右移操作符
- 位操作符:&、|、^
- 逗号表达式
二进制介绍
在初学计算机时我们常常会听到2进制、8进制、10进制、16进制…这些听着非常高级的词语,其实8进制、10进制、16进制几乎和2进制非常相似,只是稍微有一些不同,下面我们对这些进行较详细的介绍
二进制
我们举一个例子,比如用不同进制形式来表示数值15:
15的2进制:1111
15的8进制:17
15的10进制:15
15的16进制:F
我们还是先从熟悉的10进制开始讲解:
在我们学过的加减法中我们常常用这样的方式进行计算:
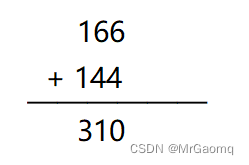
由于个位数字相加满10于是向十位数进1,而十位数也满十于是向百位数进1
因此我们从这里可以得知,所谓的十进制其实是满10进1,并且每位数字是不能超过10的
其实其他进制也相同,比如2进制
•2进制为满2进1
•2进制的数字每⼀位都是0~1的数字组成
所以1011就是15的二进制数了
2进制转10进制
10进制的123表示的值是⼀百二十三,为什么是这个值呢?其实10进制的每一位是权重的,10进制的数字从右向左是个位、十位、百位…,分别每一位的权重是10^0 , 10^1 , 10^2 …
如下图:
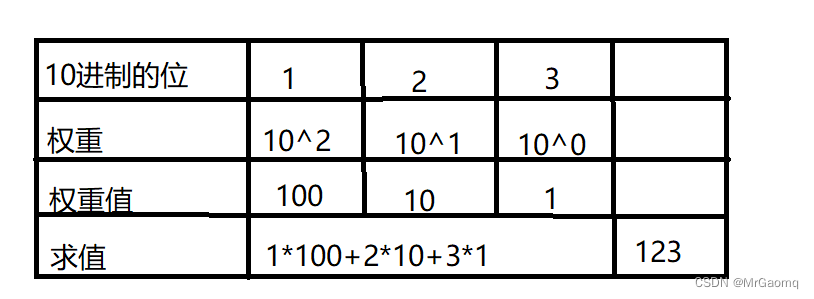
2进制和10进制是类似的,只不过2进制的每⼀位的权重,从右向左是:2^0 , 2^1 , 2 ^2…
如果是2进制的1101,该怎么理解呢?
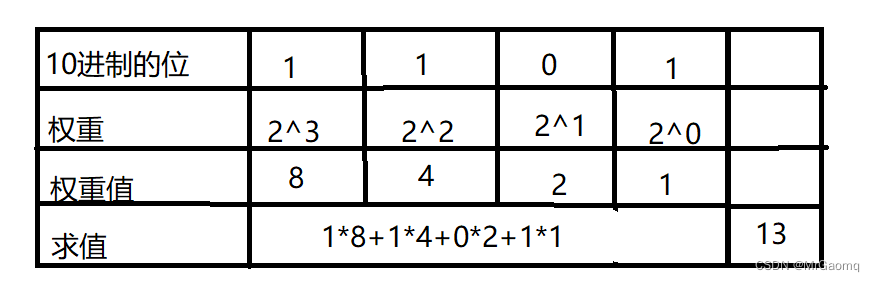
10进制转2进制数字
方法如图:
 我们只需要对125不断的除2即可得到125在2进制中的数字(其实这里我还没有完全理解为什么这样就可以得出结果,所以后期如果我想通了会在这里加上自己的理解)
我们只需要对125不断的除2即可得到125在2进制中的数字(其实这里我还没有完全理解为什么这样就可以得出结果,所以后期如果我想通了会在这里加上自己的理解)
2进制转8进制和16进制
2进制转8进制
8进制的数字每一位是0~ 7的,0~7的数字,各自写成2进制,最多有3个2进制位就足够了,比如7的二进制是111,所以在2进制转8进制数的时候,从2进制序列中右边低位开始向左每3个2进制位会换算⼀个8进制位,剩余不够3个2进制位的直接换算
如:2进制的01101011,换成8进制:0153,0开头的数组,会被当做8进制
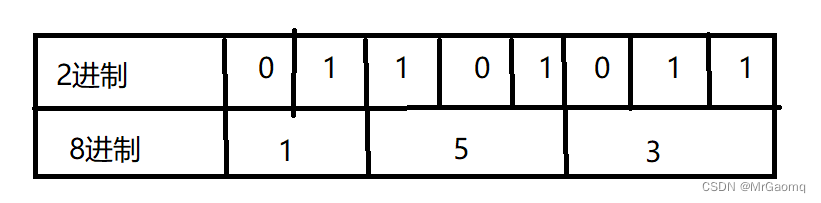
2进制转16进制
16进制的数字每⼀位是0~ 9,a~ f(10~15 )的数字,各自写成2进制,最多有4个2进制位就足够了
比如f的二进制是1111,所以在2进制转16进制数的时候,从2进制序列中右边低位开始向左每4个2进制位会换算⼀个16进制位,剩余不够4个二进制位的直接换算
如:2进制的01101011,换成16进制:0x6b,16进制表示的时候前面加0x
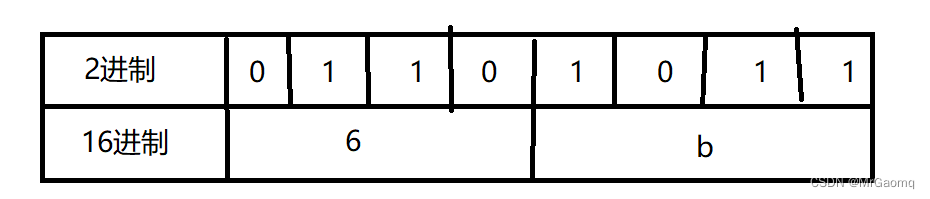
原码、反码、补码
整数的2进制表示方法有三种,即原码、反码和补码
三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位最高位的⼀位是被当做符号位,剩余的都是数值位。
正整数的原、反、补码都相同。
负整数的三种表示方法各不相同。
原码:直接将数值按照正负数的形式翻译成二进制得到的就是原码。
反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。
补码:反码+1就得到补码
对于整形来说:数据存放内存中其实存放的是补码
因为在计算机系统中,数值⼀律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统⼀处理同时,加法和减法也可以统⼀处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路
移位操作符
操作符号如下:
<<左移操作符
>>右移操作符
注:移位操作符的操作数只能是整数(因为原码、反码、补码中提到的是整数的2进制,如果是小数的话不能表示)(但是我记得好像有小数表示的方法只不过不知道能不能用在这里,可能是我没搞清楚)
左移操作符

右移操作符
移位规则:首先右移运算分两种:
1.逻辑右移:左边用0填充,右边丢弃

2.算术右移:左边用原该值的符号位填充,右边丢弃

特别提醒:对于移位运算符,不要移动负数位,这个是标准未定义的(而且也没有必要这样)
比如:
int num = 10;
num>>-1;//error
位操作符:&、|、^
位操作符有:
1.& //按位与 对应位同时为“1”时才为“1”,否则为0
2.| //按位或 对应位只要有一个为1就为1
3.^ //按位异或 对应位相同为 0,不同为 1。
注:他们的操作数必须是整数
代码如下:
#include <stdio.h>
int main()
{
int num1 = -3;
int num2 = 5;
num1 & num2;
num1 | num2;
num1 ^ num2;
return 0;
}
下面有⼀道面试题:
不能创建临时变量(第三个变量),实现两个数的交换
法一:
可能有很多人都会这样做
#include <stdio.h>
int main()
{
int a = 10;
int b = 20;
a = a+b;
b = a-b;
a = a-b;
printf("a = %d b = %d\n", a, b);
return 0;
}
这种做法有一个缺陷,就是如果a+b过大就会导致出错,因为int有范围限制,所以这种方法也要分情况用
我们看看法二:
#include <stdio.h>
int main()
{
int a = 10;
int b = 20;
a = a^b;
b = a^b;
a = a^b;
printf("a = %d b = %d\n", a, b);
return 0;
}
这种方法就很难想到了,但是也有缺陷,就是如果是有负数的话,结果就会有问题,因此这方法仅适用于正数
例题:编写代码实现:求⼀个整数存储在内存中的二进制中1的个数:
//⽅法1
#include <stdio.h>
int main()
{
int num = 10;
int count= 0;//计数
while(num)
{
if(num%2 == 1)
count++;
num = num/2;
}
printf("⼆进制中1的个数 = %d\n", count);
return 0;
}
//⽅法2:
#include <stdio.h>
int main()
{
int num = -1;
int i = 0;
int count = 0;//计数
for(i=0; i<32; i++)
{
if( num & (1 << i) )
count++;
}
printf("⼆进制中1的个数 = %d\n",count);
return 0;
}
//⽅法3:
#include <stdio.h>
int main()
{
int num = -1;
int i = 0;
int count = 0;//计数
while(num)
{
count++;
num = num&(num-1);
}
printf("⼆进制中1的个数 = %d\n",count);
return 0;
}
逗号表达式
逗号表达式,就是用逗号隔开的多个表达式。
逗号表达式,从左向右依次执行。整个表达式的结果是最后一个表达式的结果。(如果左边表达式为假就不用执行右边的表达式了)
//代码1
int a = 1;
int b = 2;
int c = (a>b, a=b+10, a, b=a+1);//逗号表达式
//代码2
if (a =b + 1, c=a / 2, d > 0)
while (a = get_val(), count_val(a), a>0)
{
..........
}