Problem - 1822E - Codeforces

题意：

 

思路：

简单复盘一下思路

首先，n为奇数或有一种字符出现次数> n / 2就无解的结论是可以根据样例看出来的

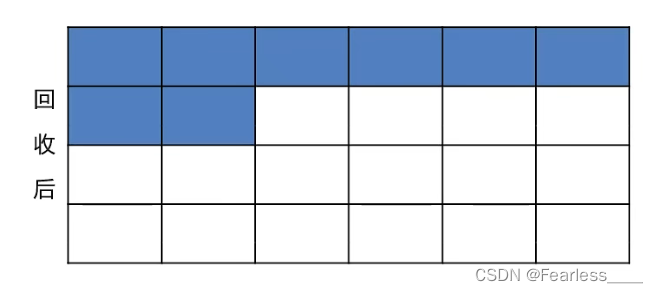
然后就显然的发现，每2个不同的回文对有1的贡献

 那么这样匹配之后会有剩余的回文对，这些回文对一定是和另两种字符的反回文对匹配

然后就开始想歪了

 

剩余的这些回文对和前面匹配好的反回文对匹配就行，且一定足够消化这些回文对

首先，回文对的字符种类一定是 >= 3的，除去那种两种字符且每种回文对的出现次数一样的情况

因为这个出现次数最多的回文对的出现次数 <= s / 2，s是总的出现次数

那么前面匹配好的反回文对一定足以消化剩余的回文对

这样贡献就是cnt_mx

还有就是内部消化，贡献就是（res + 1) / 2

取max即可

Code：

#include <bits/stdc++.h>

#define int long long

using i64 = long long;

constexpr int N = 2e5 + 10;
constexpr int mod = 998244353;

int num[30], cnt[30];

void solve() {
	for (int i = 0; i <= 29; i ++) {
		num[i] = cnt[i] = 0;
	}
	int n;
	std::string s;

	std::cin >> n >> s;
	s = " " + s;

	int mx = 0;
	for (int i = 1; i <= n; i ++) {
		num[s[i] - 'a' + 1] ++;
		mx = std::max(mx, num[s[i] - 'a' + 1]);
	}

	if (n % 2 == 1 || mx > n / 2) {
		std::cout << -1 << "\n";
		return;
	}

	int res = 0;
	for (int i = 1; i <= n / 2; i ++) {
		if (s[i] == s[n - i + 1]) {
			res ++;
			cnt[s[i] - 'a' + 1] ++;
		}
	}

	int cnt_mx = 0;
	for (int i = 1; i <= 26; i ++) {
		cnt_mx = std::max(cnt_mx, cnt[i]);
	}

	std::cout << std::max(cnt_mx, (res + 1) / 2) << "\n";
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t = 1;
	std::cin >> t;

    while (t--) {
        solve();
    }
    
    return 0;
}