版本说明

当前版本号[20230816]。

版本	修改说明
20230816	初版

目录

数组总结篇

数组理论基础

数组是非常基础的数据结构，在面试中，考察数组的题目一般在思维上都不难，主要是考察对代码的掌控能力

也就是说，想法很简单，但实现起来 可能就不是那么回事了。

首先要知道数组在内存中的存储方式，这样才能真正理解数组相关的面试题

数组是存放在连续内存空间上的相同类型数据的集合。

数组可以方便的通过下标索引的方式获取到下标下对应的数据。

举一个字符数组的例子，如图所示：

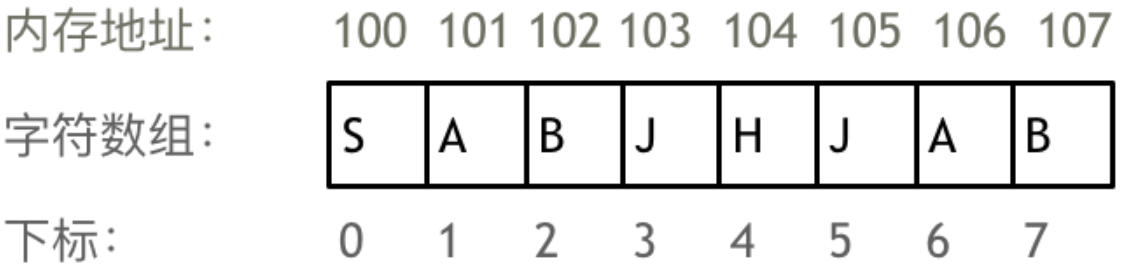
需要两点注意的是

• 数组下标都是从0开始的。
• 数组内存空间的地址是连续的

正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：

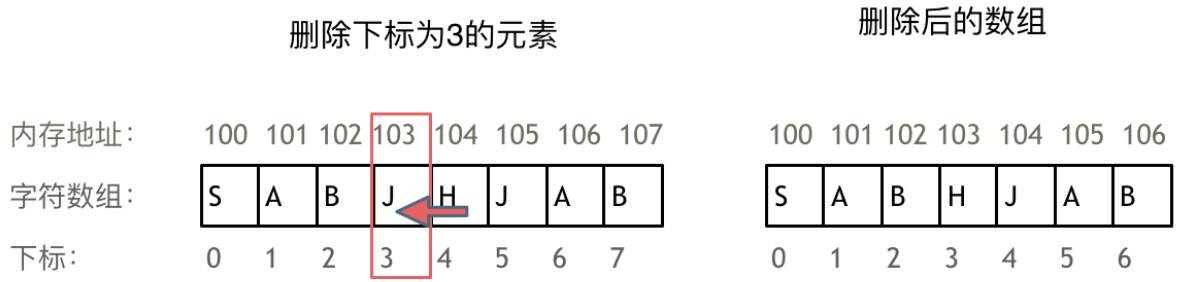
在C++中，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。

数组的元素是不能删的，只能覆盖。

那么二维数组直接上图，大家应该就知道怎么回事了

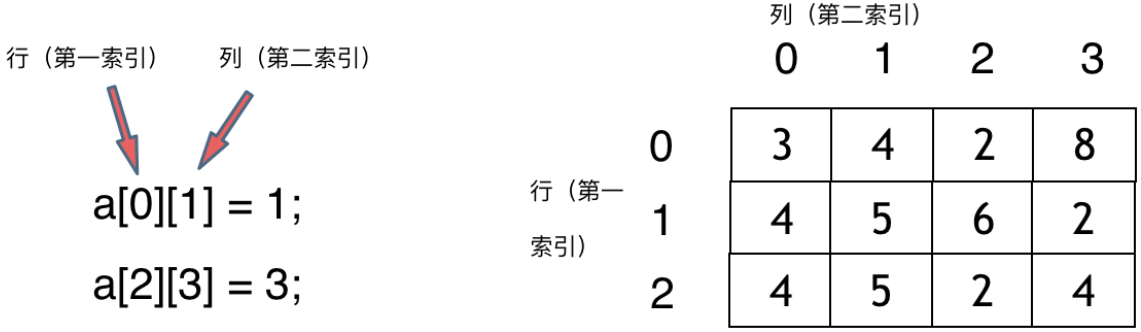
那么二维数组在内存的空间地址是连续的么？

我们来举一个Java的例子，例如： int[][] rating = new int[3][4]; ， 这个二维数组在内存空间可不是一个 3*4 的连续地址空间

看了下图，就应该明白了：

所以Java的二维数组在内存中不是 3\*4 的连续地址空间，而是四条连续的地址空间组成！

数组的经典题目

在面试中，数组是必考的基础数据结构。

其实数组的题目在思想上一般比较简单的，但是如果想高效，并不容易。

我们之前一共讲解了四道经典数组题目，每一道题目都代表一个类型，一种思想。

二分法

可点击此处，跳转->力扣算法题：704二分查找.Java版（示例代码与导图详解）

这道题目呢，考察数组的基本操作，思路很简单，但是通过率在简单题里并不高，不要轻敌。

可以使用暴力解法，通过这道题目，如果追求更优的算法，建议试一试用二分法，来解决这道题目

• 暴力解法时间复杂度：O(n)
• 二分法时间复杂度：O(logn)

在这道题目中我们讲到了循环不变量原则，只有在循环中坚持对区间的定义，才能清楚的把握循环中的各种细节。

二分法是算法面试中的常考题，建议通过这道题目，锻炼自己手撕二分的能力。

双指针法

可点击此处，跳转->力扣算法题：27移除元素.Java版（示例代码与导图详解）
可点击此处，跳转->力扣算法题：977有序数组的平方.Java版（示例代码与导图详解）

双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

• 暴力解法时间复杂度：O(n^2)
• 双指针时间复杂度：O(n)

这道题目迷惑了不少同学，纠结于数组中的元素为什么不能删除，主要是因为以下两点：

• 数组在内存中是连续的地址空间，不能释放单一元素，如果要释放，就是全释放（程序运行结束，回收内存栈空间）。
• C++中vector和array的区别一定要弄清楚，vector的底层实现是array，封装后使用更友好。

双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组和链表操作的面试题，都使用双指针法。

滑动窗口

可点击此处，跳转->力扣算法题：209长度最小的子数组.Java版（示例代码与导图详解）

本题介绍了数组操作中的另一个重要思想：滑动窗口。

• 暴力解法时间复杂度：O(n^2)
• 滑动窗口时间复杂度：O(n)

本题中，主要要理解滑动窗口如何移动 窗口起始位置，达到动态更新窗口大小的，从而得出长度最小的符合条件的长度。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。

如果没有接触过这一类的方法，很难想到类似的解题思路，滑动窗口方法还是很巧妙的。

模拟行为

可点击此处，跳转->力扣算法题：59螺旋矩阵II.Java版（示例代码与导图详解）

模拟类的题目在数组中很常见，不涉及到什么算法，就是单纯的模拟，十分考察大家对代码的掌控能力。

在这道题目中，我们再一次介绍到了循环不变量原则，其实这也是写程序中的重要原则。

相信大家有遇到过这种情况： 感觉题目的边界调节超多，一波接着一波的判断，找边界，拆了东墙补西墙，好不容易运行通过了，代码写的十分冗余，毫无章法，其实真正解决题目的代码都是简洁的，或者有原则性的，大家可以在这道题目中体会到这一点。

总结

1. 二分查找（Binary Search）：适用于已排序的数组。通过将数组**不断二分为两部分，缩小查找范围，快速定位目标元素的位置。**这是一种高效的查找方法，时间复杂度为O(log n)。
2. 移除元素（Remove Element）：**目标是移除数组中指定的元素，并返回新数组的长度。**可以使用双指针的方法，一个指针用于遍历数组，另一个指针指向当前要保留的元素。时间复杂度为O(n)，其中n是数组的长度。
3. 螺旋数组（Spiral Array）：**给定一个二维矩阵，按照顺时针螺旋顺序依次输出所有元素。**可以使用模拟的方法，按照规定的遍历顺序将元素加入结果数组。时间复杂度为O(m*n)，其中m和n分别是矩阵的行数和列数。
4. 最小覆盖子串（Minimum Window Substring）：**给定一个字符串和一个目标子串，在字符串中找到一个最短的子串，使得该子串包含目标子串中的所有字符。**通常使用滑动窗口的方法，在滑动过程中动态调整窗口的大小，找到最短的满足条件的子串。时间复杂度为O(m+n)，其中m和n分别是字符串和目标子串的长度。
5. 长度最小的数组（Minimum Length Subarray）：**给定一个数组和一个目标值，找到长度最小的子数组，使得子数组的元素和大于等于目标值。**可以使用滑动窗口的方法，在滑动过程中动态调整窗口的大小，找到最小的满足条件的子数组。时间复杂度为O(n)，其中n是数组的长度。
6. 有序数组的平方（Squares of a Sorted Array）：**给定一个有序数组，返回一个新数组，新数组中的元素为原数组元素的平方，并且新数组也是有序的。**可以使用双指针的方法，从数组的两端向中间遍历，并将平方后的较大值放入新数组的末尾。时间复杂度为O(n)，其中n是数组的长度。