LeetCode236. 二叉树的最近公共祖先

news2025/1/10 11:19:10

236. 二叉树的最近公共祖先

文章目录

- - [236. 二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)
  - - 一、题目
    - 二、题解
    - - 方法一：递归构建祖先数组
      - 方法二：一个非常方便的递归

一、题目

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

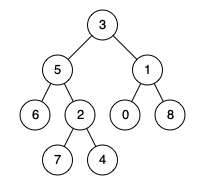
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

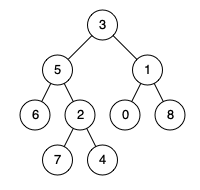
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

二、题解

方法一：递归构建祖先数组

当解决这类二叉树相关的问题时，我们可以考虑使用递归来遍历树的节点。在这个问题中，我们需要找到两个指定节点的最近公共祖先，可以考虑从根节点开始递归地往下搜索。下面是一个详细的解题思路：

算法思路

我们从根节点开始递归遍历树，查找指定的节点p和q。
使用一个递归函数 findAncestor，它将用于找到一个节点的所有祖先节点。我们使用两个vector分别保存节点p和q的所有祖先节点。
在递归遍历的过程中，一旦找到了节点p或q，我们将停止继续递归并且将flag设置为true，以便在后续递归中可以直接返回而不继续递归。
在 findAncestor 中，我们首先递归地遍历左子树，然后递归地遍历右子树。如果已经找到了节点p或q（flag为true），或者当前节点就是目标节点之一，我们将当前节点添加到对应的祖先节点vector中，并将flag设置为true。
于是乎，在递归回溯过程中目标节点的祖先节点会不断进入祖先数组节点vector（所以最后得到的数组是倒序的）。
在 lowestCommonAncestor 函数中，我们先使用 findAncestor 分别找到节点p和q的所有祖先节点。
然后，我们遍历这两个祖先节点vector，寻找第一个在两个vector中都出现的节点。这个节点就是两个指定节点的最近公共祖先。

具体实现

class Solution {
public:
    TreeNode* pre = nullptr;
    bool flag = false;
    
    // 递归函数，用于查找节点的所有祖先节点
    void findAncestor(vector<TreeNode*>& ances, TreeNode* root, TreeNode* target) {
        if (root == nullptr) return;
        if (flag) return; 
        
        // 递归遍历左子树
        findAncestor(ances, root->left, target);
        // 递归遍历右子树
        findAncestor(ances, root->right, target);
        
        // 如果flag为true，表示已经找到目标节点，或者当前节点就是目标节点之一
        if (flag || root == target) {
            // 将当前节点添加到祖先节点vector中
            ances.push_back(root);
            // 设置flag为true，以便在后续递归中可以直接返回
            flag = true;  
        }
    }

    // 主函数，寻找两个指定节点的最近公共祖先
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode* result = nullptr;
        vector<TreeNode*> ancesP;
        vector<TreeNode*> ancesQ;
        
        if (root == nullptr) return result;
        
        // 找到节点p的所有祖先节点
        findAncestor(ancesP, root, p);
        flag = false; 
        // 找到节点q的所有祖先节点
        findAncestor(ancesQ, root, q);
        
        // 遍历节点p的祖先节点
        for (int i = 0; i < ancesP.size() && result == nullptr; i++) {
            // 遍历节点q的祖先节点
            for (int j = 0; j < ancesQ.size(); j++) {
                // 如果在两个祖先节点vector中找到相同的节点，就是最近公共祖先
                if (ancesP[i] == ancesQ[j]) {
                    result = ancesP[i];
                    break;
                }
            }
        }
        return result;
    }
};

算法分析

时间复杂度：遍历树的过程中，每个节点都会被访问一次，所以时间复杂度为O(n)，其中n是树中的节点数。
空间复杂度：递归栈的深度最多为树的高度，而空间复杂度取决于递归栈的最大深度，所以空间复杂度为O(h)，其中h是树的高度。此外，用于存储祖先节点的vector也会占用一些空间。

错误历程

第一次写出来的时候犯了一些错误，花了很久才改过来，代码是这样的，错误原因写在了里面：

class Solution {
public:
    TreeNode* pre = nullptr;
    bool flag = false;
    
    void findAncestor(vector<TreeNode*>& ances, TreeNode* root, int target) {
        if (root == nullptr) return;
        findAncestor(ances, root->left, target);
        flag = false;//首先代码是基于后序遍历的。加了这行以后如果target在左子树，最后祖先数组会少根节点（调试就可以调试出来），但是不加这行更是错误，因为target在左子树的话连右子树节点都会成为其祖先节点，所以最好的方案是上面答案前面加上if (flag) return; 然后lowCommonAncestor中两个findAncestor之间重置一下flag，啥问题都解决了。
        findAncestor(ances, root->right, target);
        if (flag) {
            ances.push_back(root);
            return;
        }
        if (root->val == target) {
            ances.push_back(root);
            flag = true;
            return;
        }
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode* result = nullptr;
        vector<TreeNode*> ancesP;
        vector<TreeNode*> ancesQ;
        
        if (root == nullptr) return result;
        
        findAncestor(ancesP, root, p->val);
        findAncestor(ancesQ, root, q->val);
        
        for (int i = 0; i < ancesP.size(); i++) {
            for (int j = 0; j < ancesQ.size(); j++) {
                if (ancesP[i] == ancesQ[j]) {
                    result = ancesP[i];
                    return result;
                }
            }
        }
        return result;
    }
};

方法二：一个非常方便的递归

只能说很巧妙……

算法思路

递归的终止条件： 首先，我们需要考虑递归的终止条件。如果当前节点为空，或者当前节点是要找的两个节点之一，那么直接返回当前节点。这是因为，当节点为空时，肯定不存在公共祖先；而当节点等于要找的节点之一时，该节点自身就是最近公共祖先。
递归搜索左右子树： 若不满足终止条件，说明当前节点既不为空，也不是要找的节点之一。我们需要递归地搜索左子树和右子树，来寻找节点p和q的最近公共祖先。
递归合并结果： 在搜索左右子树之后，我们可以获得左子树和右子树分别关于节点p和q的最近公共祖先。如果左右子树的结果都不为空，说明节点p和q分别位于左右子树的不同侧，而当前节点就是最近公共祖先。如果左子树的结果不为空，而右子树的结果为空，说明两个节点都在左子树上，最近公共祖先就在左子树中。如果左子树的结果为空，而右子树的结果不为空，情况类似。

具体实现

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 递归终止条件：节点为空或节点是要找的节点之一
        if (root == nullptr || root == p || root == q) {
            return root;
        }

        // 递归搜索左右子树
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        // 递归合并结果
        if (left && right) {
            return root;
        } else if (left) {
            return left;
        } else {
            return right;
        }
    }
};