目录

背包理论基础

 动态规划五步曲：

1.确定dp[i][j]的含义

2.找出递推公式

3.初始化dp数组

4.确定遍历顺序

5.举例dp数组

背包理论基础II 

动态规划五步曲：

1.确定dp[j]含义

2.找出递推公式

3.初始化dp数组

4.确定遍历顺序

5.举例dp数组

LeetCode 416.分割等和子集

动态规划五步曲：

1.确定dp[i]的含义

2.找出递推公式

3.初始化dp数组

4.确定遍历方向

5.举例dp数组 

---

背包理论基础

文章讲解：代码随想录

视频讲解：带你学透0-1背包问题！| 关于背包问题，你不清楚的地方，这里都讲了！| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili

 动态规划五步曲：

1.确定dp[i][j]的含义

 dp[i][j]:把第i个物品放进容量为j的背包时，有最大价值为dp[i][j]

2.找出递推公式

dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]);

3.初始化dp数组

初始化dp[0][j] = value[i];

4.确定遍历顺序

从前往后

5.举例dp数组

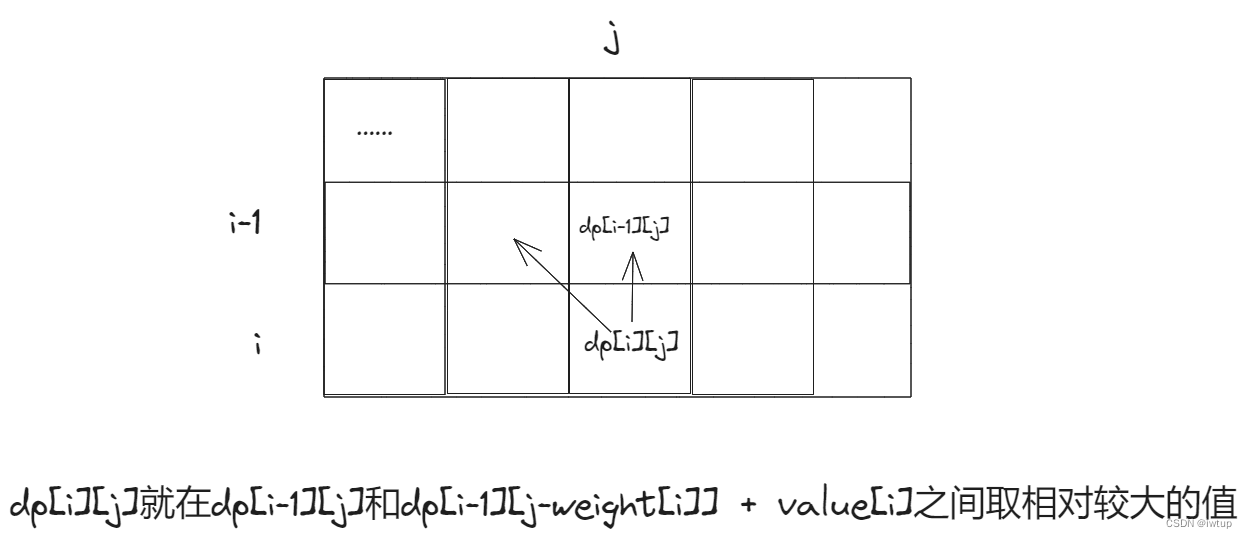
代码如下（Java）：

public class BagProblem {
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testWeightBagProblem(weight,value,bagSize);
    }

    /**
     * 动态规划获得结果
     * @param weight  物品的重量
     * @param value   物品的价值
     * @param bagSize 背包的容量
     */
    public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){

        // 创建dp数组
        int goods = weight.length;  // 获取物品的数量
        int[][] dp = new int[goods][bagSize + 1];

        // 初始化dp数组
        // 创建数组后，其中默认的值就是0
        for (int j = weight[0]; j <= bagSize; j++) {
            dp[0][j] = value[0];
        }

        // 填充dp数组
        for (int i = 1; i < weight.length; i++) {
            for (int j = 1; j <= bagSize; j++) {
                if (j < weight[i]) {
                    /**
                     * 当前背包的容量都没有当前物品i大的时候，是不放物品i的
                     * 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
                     */
                    dp[i][j] = dp[i-1][j];
                } else {
                    /**
                     * 当前背包的容量可以放下物品i
                     * 那么此时分两种情况：
                     *    1、不放物品i
                     *    2、放物品i
                     * 比较这两种情况下，哪种背包中物品的最大价值最大
                     */
                    dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
                }
            }
        }

        // 打印dp数组
        for (int i = 0; i < goods; i++) {
            for (int j = 0; j <= bagSize; j++) {
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println("\n");
        }
    }
}

背包理论基础II 

文章讲解：代码随想录

视频讲解：带你学透01背包问题（滚动数组篇） | 从此对背包问题不再迷茫！_哔哩哔哩_bilibili 

动态规划五步曲：

1.确定dp[j]含义

dp[j]:重量为j的背包最大价值为dp[j]

2.找出递推公式

dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);

3.初始化dp数组

全部初始化为非负数的最小值

4.确定遍历顺序

遍历物品为从前往后，遍历重量为从后往前

5.举例dp数组

 

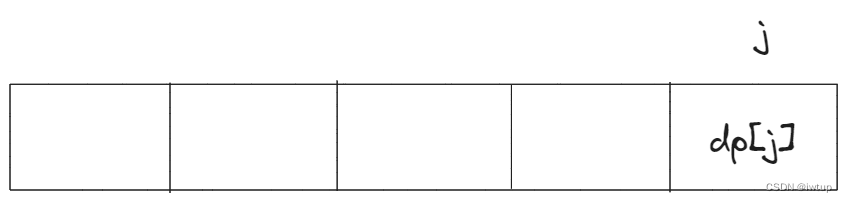
代码如下（Java）：

    public static void main(String[] args) {
        int[] weight = {1, 3, 4};
        int[] value = {15, 20, 30};
        int bagWight = 4;
        testWeightBagProblem(weight, value, bagWight);
    }

    public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
        int wLen = weight.length;
        //定义dp数组：dp[j]表示背包容量为j时，能获得的最大价值
        int[] dp = new int[bagWeight + 1];
        //遍历顺序：先遍历物品，再遍历背包容量
        for (int i = 0; i < wLen; i++){
            for (int j = bagWeight; j >= weight[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
        //打印dp数组
        for (int j = 0; j <= bagWeight; j++){
            System.out.print(dp[j] + " ");
        }
    }

---

LeetCode 416.分割等和子集

文章讲解：代码随想录

视频讲解：动态规划之背包问题，这个包能装满吗？| LeetCode：416.分割等和子集_哔哩哔哩_bilibili

力扣题目：LeetCode 416.分割等和子集

 

关键在于把分割等和子集抽象为背包问题。第一：分割两个等和子集会在该子集元素总和为偶数的前提上进行的。第二：那么我们可以把子集元素总和分割成一半为target，这一半target就作为背包问题中的背包重量。第三：子集元素看成背包问题中的物品价值以及物品总量。最后，比较target和dp[target]。

动态规划五步曲：

1.确定dp[i]的含义

dp[i]:容量为i的最大价值为dp[i]

2.找出递推公式

dp[i] = Math.max(dp[i], dp[i-nums[i]] + nums[i]);

3.初始化dp数组

dp数组全部初始化为非负整数的最小值

4.确定遍历方向

从前往后

5.举例dp数组 

代码如下（Java）：

class Solution {
    public boolean canPartition(int[] nums) {

        int n = nums.length;
        int sum = 0;

        for(int num : nums) sum += num;

        if(sum % 2 != 0)    return false;

        int target = sum / 2;
        int[] dp = new int[target + 1];

        for(int i = 0; i < n; i++){
            for(int j = target; j >= nums[i]; j--){
                dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i]);
            }

            if(target == dp[target]) return true;
        }

        return target == dp[target];
    }
}