文章目录

DFS 和 BFS
BFS 的应用一：层序遍历
BFS 的应用二：最短路径
- 最短路径例题讲解
DFS简介
DFS原理分类与分析
- 1. DFS连通性模型
- 2. DFS思路应用-穷举求解问题

DFS（深度优先搜索）和 BFS（广度优先搜索）就像孪生兄弟，提到一个总是想起另一个。然而在实际使用中，我们用 DFS 的时候远远多于 BFS。那么，是不是 BFS 就没有什么用呢？

如果我们使用 DFS/BFS 只是为了遍历一棵树、一张图上的所有结点的话，那么 DFS 和 BFS 的能力没什么差别，我们当然更倾向于更方便写、空间复杂度更低的 DFS 遍历。不过，某些使用场景是 DFS 做不到的，只能使用 BFS 遍历。这就是本文要介绍的两个场景：「层序遍历」、「最短路径」。

DFS 和 BFS

先看看在二叉树上进行 DFS 遍历和 BFS 遍历的代码比较。
DFS 遍历使用递归：

void dfs(TreeNode root){
	if (root == null) { return; }
    dfs(root.left);
    dfs(root.right);
}

BFS 遍历使用队列数据结构：

void bfs(TreeNode root) {
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll(); // Java 的 pop 写作 poll()
        if (node.left != null) {
            queue.add(node.left);
        }
        if (node.right != null) {
            queue.add(node.right);
        }
    }
}

只是比较两段代码的话，最直观的感受就是：DFS 遍历的代码比 BFS 简洁太多了！这是因为递归的方式隐含地使用了系统的栈，我们不需要自己维护一个数据结构。如果只是简单地将二叉树遍历一遍，那么 DFS 显然是更方便的选择。

虽然 DFS 与 BFS 都是将二叉树的所有结点遍历了一遍，但它们遍历结点的顺序不同。
在这里插入图片描述
这个遍历顺序也是 BFS 能够用来解「层序遍历」、「最短路径」问题的根本原因。下面，我们结合几道例题来讲讲 BFS 是如何求解层序遍历和最短路径问题的。

BFS 的应用一：层序遍历

LeetCode 102. Binary Tree Level Order Traversal 二叉树的层序遍历（Medium）

给定一个二叉树，返回其按层序遍历得到的节点值。层序遍历即逐层地、从左到右访问所有结点。

什么是层序遍历呢？简单来说，层序遍历就是把二叉树分层，然后每一层从左到右遍历：
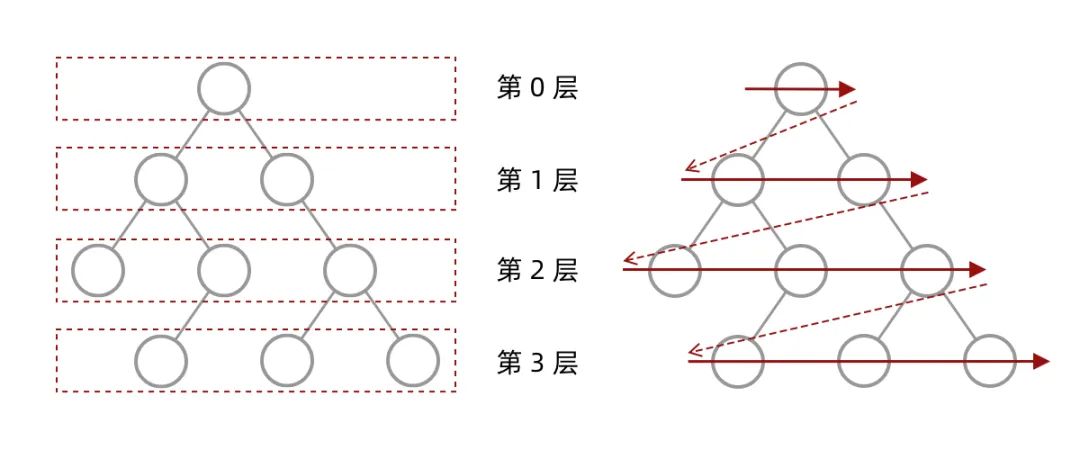
二叉树的层序遍历

乍一看来，这个遍历顺序和 BFS 是一样的，我们可以直接用 BFS 得出层序遍历结果。然而，层序遍历要求的输入结果和 BFS 是不同的。层序遍历要求我们区分每一层，也就是返回一个二维数组。而 BFS 的遍历结果是一个一维数组，无法区分每一层。
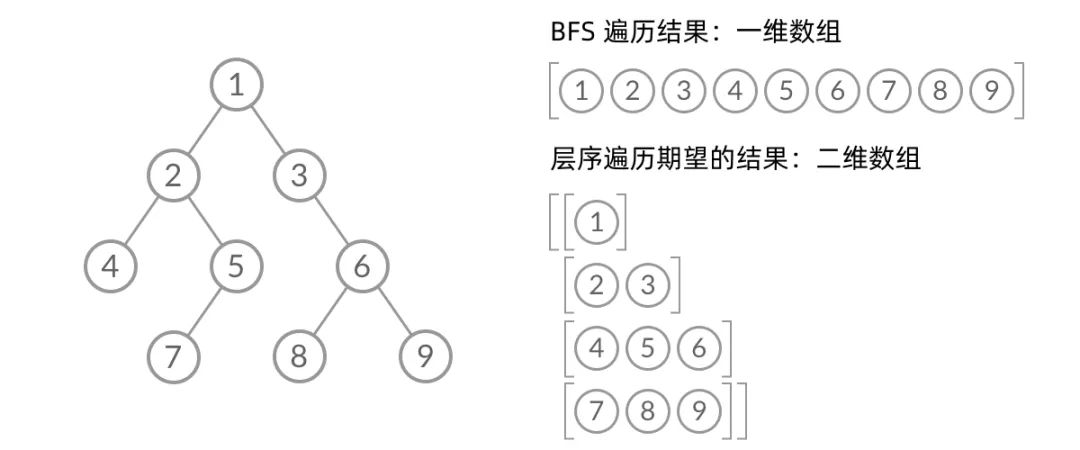
BFS 遍历与层序遍历的输出结果不同
那么，怎么给 BFS 遍历的结果分层呢？我们首先来观察一下 BFS 遍历的过程中，结点进队列和出队列的过程：
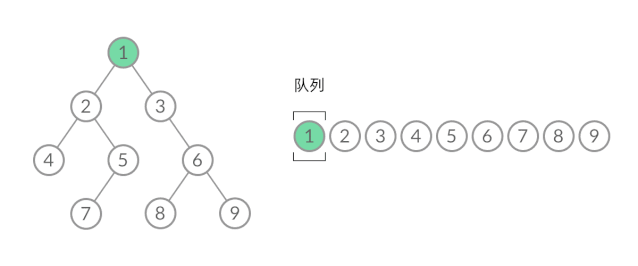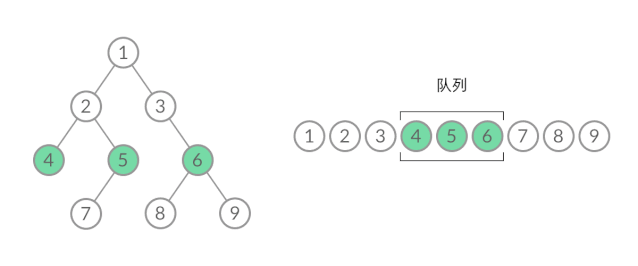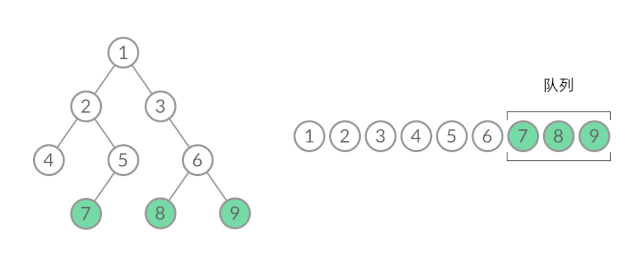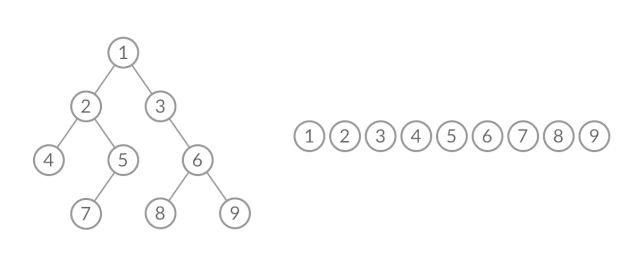
在这里插入图片描述
截取 BFS 遍历过程中的某个时刻：

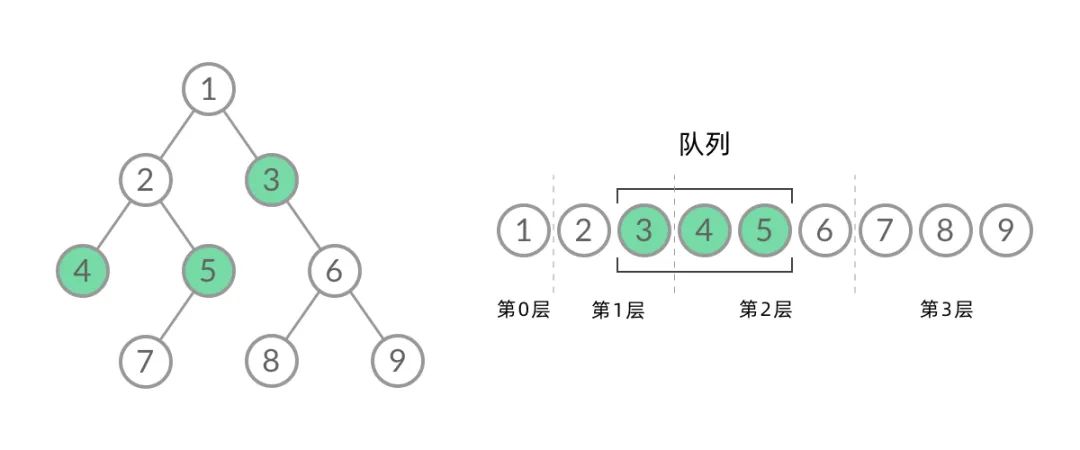
可以看到，此时队列中的结点是 3、4、5，分别来自第 1 层和第 2 层。这个时候，第 1 层的结点还没出完，第 2 层的结点就进来了，而且两层的结点在队列中紧挨在一起，我们无法区分队列中的结点来自哪一层。

因此，我们需要稍微修改一下代码，在每一层遍历开始前，先记录队列中的结点数量 n（也就是这一层的结点数量），然后一口气处理完这一层的 n 个结点。

// 二叉树的层序遍历
void bfs(TreeNode root) {
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int n = queue.size();
        for (int i = 0; i < n; i++) { 
            // 变量 i 无实际意义，只是为了循环 n 次
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
    }
}

这样，我们就将 BFS 遍历改造成了层序遍历。在遍历的过程中，结点进队列和出队列的过程为：
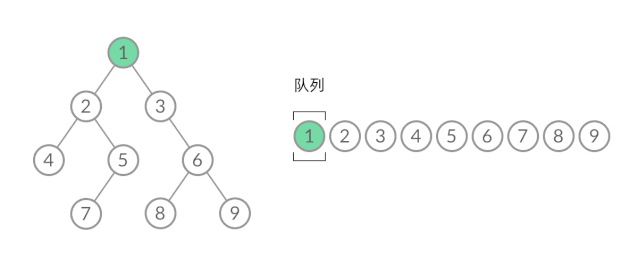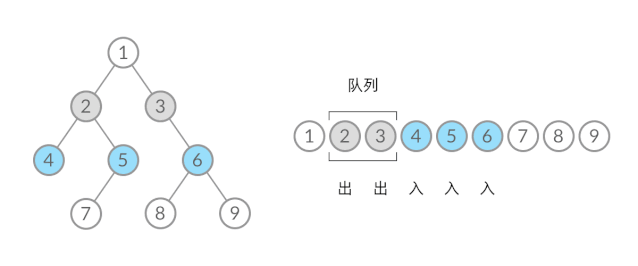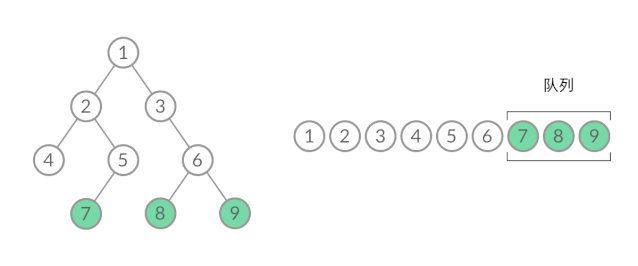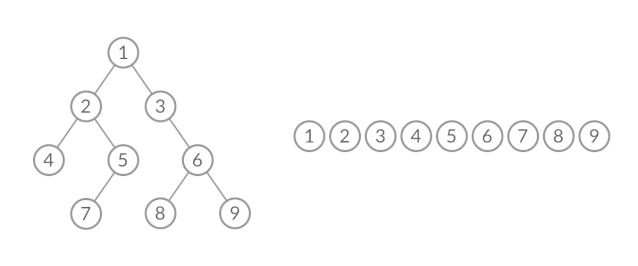
在这里插入图片描述
可以看到，在 while 循环的每一轮中，都是将当前层的所有结点出队列，再将下一层的所有结点入队列，这样就实现了层序遍历。

最终我们得到的题解代码为：

public List<List<Integer>> levelOrder(TreeNode root) {
    List<List<Integer>> res = new ArrayList<>();

    Queue<TreeNode> queue = new ArrayDeque<>();
    if (root != null) {
        queue.add(root);
    }
    while (!queue.isEmpty()) {
        int n = queue.size();
        List<Integer> level = new ArrayList<>();
        for (int i = 0; i < n; i++) { 
            TreeNode node = queue.poll();
            level.add(node.val);
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
        res.add(level);
    }

    return res;
}

BFS 的应用二：最短路径

在一棵树中，一个结点到另一个结点的路径是唯一的，但在图中，结点之间可能有多条路径，其中哪条路最近呢？这一类问题称为最短路径问题。最短路径问题也是 BFS 的典型应用，而且其方法与层序遍历关系密切。

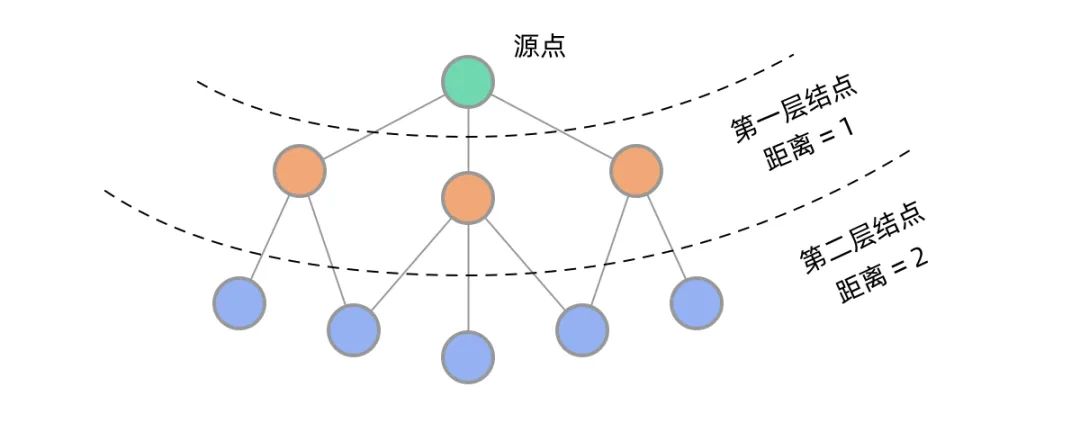
在二叉树中，BFS 可以实现一层一层的遍历。在图中同样如此。从源点出发，BFS 首先遍历到第一层结点，到源点的距离为 1，然后遍历到第二层结点，到源点的距离为 2…… 可以看到，用 BFS 的话，距离源点更近的点会先被遍历到，这样就能找到到某个点的最短路径了。
在这里插入图片描述

小贴士：
很多同学一看到「最短路径」，就条件反射地想到「Dijkstra 算法」。为什么 BFS 遍历也能找到最短路径呢？
这是因为，Dijkstra 算法解决的是带权最短路径问题，而我们这里关注的是无权最短路径问题。也可以看成每条边的权重都是 1。这样的最短路径问题，用 BFS 求解就行了。
在面试中，你可能更希望写 BFS 而不是 Dijkstra。毕竟，敢保证自己能写对 Dijkstra 算法的人不多。

最短路径问题属于图算法。由于图的表示和描述比较复杂，本文用比较简单的网格结构代替。网格结构是一种特殊的图，它的表示和遍历都比较简单，适合作为练习题。在 LeetCode 中，最短路径问题也以网格结构为主。

最短路径例题讲解

LeetCode 1162. As Far from Land as Possible 离开陆地的最远距离（Medium）

你现在手里有一份大小为 n*n 的地图网格 grid，上面的每个单元格都标记为 0 或者 1，其中 0 代表海洋，1 代表陆地，请你找出一个海洋区域，这个海洋区域到离它最近的地区域的距离是最大的。
我们这里说的距离是「曼哈顿距离。 $x_0, y_0)$ 和 $x_1, y_1)$ 这两个区域之间的距离是 $x_0-x_1|+|y_0-y_1|$ 。
如果我们的地图上只有陆地或者海洋，请返回 -1。

这道题就是一个在网格结构中求最短路径的问题。同时，它也是一个「岛屿问题」，即用网格中的 1 和 0 表示陆地和海洋，模拟出若干个岛屿。
在上一篇文章中，我们介绍了网格结构的基本概念，以及网格结构中的 DFS 遍历。其中一些概念和技巧也可以用在 BFS 遍历中：

格子 (r, c)的相邻四个格子为：(r-1, c)、(r+1, c)、(r, c-1) 和 (r, c+1)；
使用函数inArea判断当前格子的坐标是否在网格范围内；
将遍历过的格子标记为 2，避免重复遍历。

上一篇文章讲过了网格结构 DFS 遍历，这篇文章正好讲解一下网格结构的 BFS 遍历。要解最短路径问题，我们首先要写出层序遍历的代码，仿照上面的二叉树层序遍历代码，类似地可以写出网格层序遍历：

// 网格结构的层序遍历
// 从格子 (i, j) 开始遍历
void bfs(int[][] grid, int i, int j) {
    Queue<int[]> queue = new ArrayDeque<>();
    queue.add(new int[]{r, c});
    while (!queue.isEmpty()) {
        int n = queue.size();
        for (int i = 0; i < n; i++) { 
            int[] node = queue.poll();
            int r = node[0];
            int c = node[1];
            if (r-1 >= 0 && grid[r-1][c] == 0) {
                grid[r-1][c] = 2;
                queue.add(new int[]{r-1, c});
            }
            if (r+1 < N && grid[r+1][c] == 0) {
                grid[r+1][c] = 2;
                queue.add(new int[]{r+1, c});
            }
            if (c-1 >= 0 && grid[r][c-1] == 0) {
                grid[r][c-1] = 2;
                queue.add(new int[]{r, c-1});
            }
            if (c+1 < N && grid[r][c+1] == 0) {
                grid[r][c+1] = 2;
                queue.add(new int[]{r, c+1});
            }
        }
    }
}

以上的层序遍历代码有几个注意点：

队列中的元素类型是int[]数组，每个数组的长度为 2，包含格子的行坐标和列坐标。
为了避免重复遍历，这里使用到了和 DFS 遍历一样的技巧：把已遍历的格子标记为 2。注意：我们在将格子放入队列之前就将其标记为2。想一想，这是为什么？
在将格子放入队列之前就检查其坐标是否在网格范围内，避免将「不存在」的格子放入队列。

这段网格遍历代码还有一些可以优化的地方。由于一个格子有四个相邻的格子，代码中判断了四遍格子坐标的合法性，代码稍微有点啰嗦。我们可以用一个 moves 数组存储相邻格子的四个方向：

int[][] moves = {
    {-1, 0}, {1, 0}, {0, -1}, {0, 1},
};

然后把四个 if 判断变成一个循环：

for (int[][] move : moves) {
    int r2 = r + move[0];
    int c2 = c + move[1];
    if (inArea(grid, r2, c2) && grid[r2][c2] == 0) {
        grid[r2][c2] = 2;
        queue.add(new int[]{r2, c2});
    }
}

写好了层序遍历的代码，接下来我们看看如何来解决本题中的最短路径问题。

这道题要找的是距离陆地最远的海洋格子。假设网格中只有一个陆地格子，我们可以从这个陆地格子出发做层序遍历，直到所有格子都遍历完。最终遍历了几层，海洋格子的最远距离就是几。 (下图为:从单个陆地格子出发的距离（动图）)
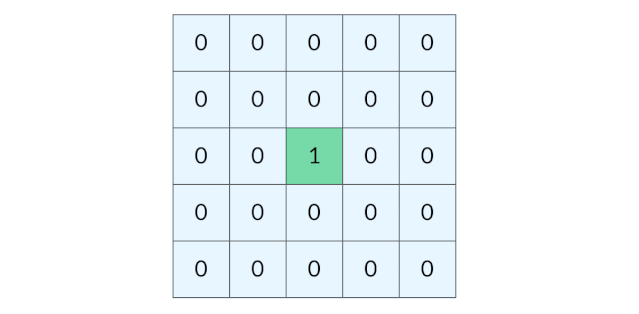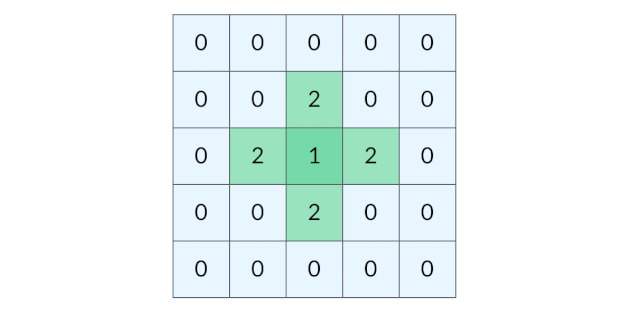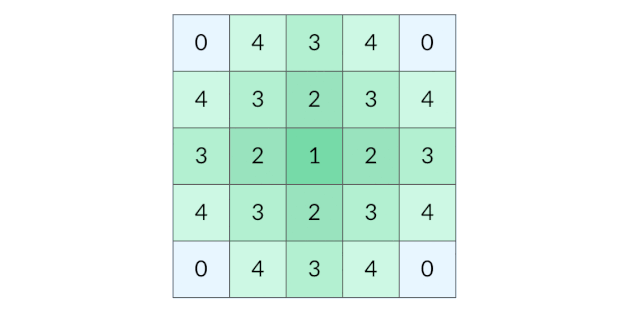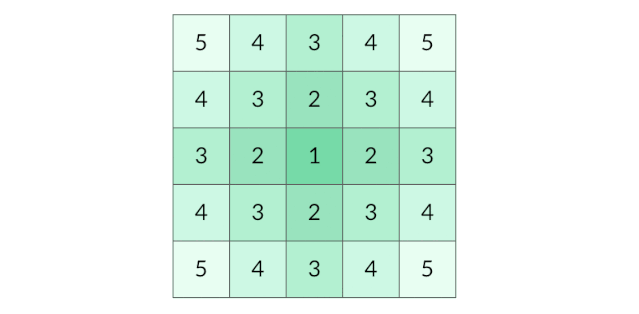
在这里插入图片描述
那么有多个陆地格子的时候怎么办呢？一种方法是将每个陆地格子都作为起点做一次层序遍历，但是这样的时间开销太大。

BFS 完全可以以多个格子同时作为起点。我们可以把所有的陆地格子同时放入初始队列，然后开始层序遍历，这样遍历的效果如下图所示：
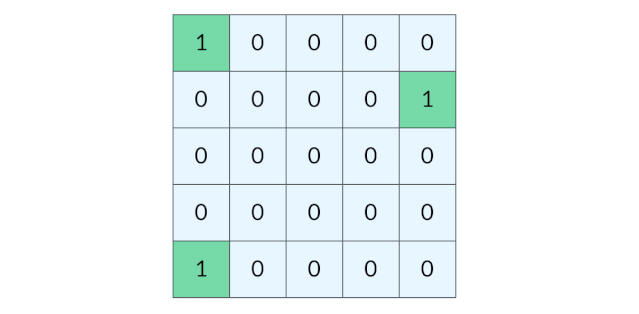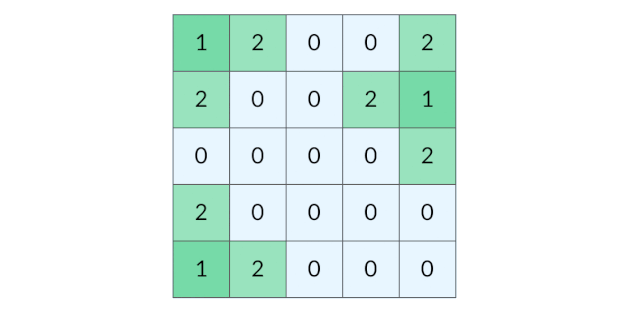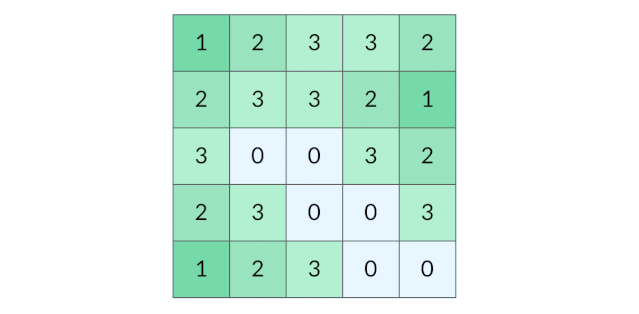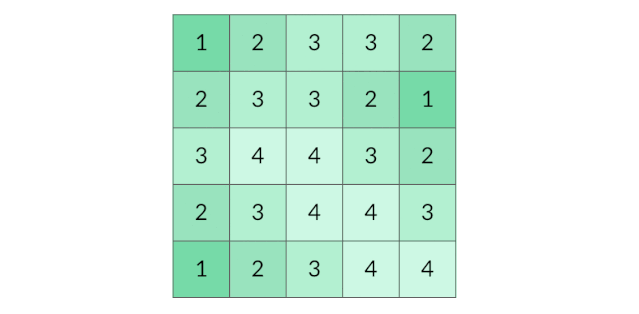
在这里插入图片描述
这种遍历方法实际上叫做「多源 BFS」。多源 BFS 的定义不是今天讨论的重点，你只需要记住多源 BFS 很方便，只需要把多个源点同时放入初始队列即可。

需要注意的是，虽然上面的图示用 1、2、3、4 表示层序遍历的层数，但是在代码中，我们不需要给每个遍历到的格子标记层数，只需要用一个distance变量记录当前的遍历的层数（也就是到陆地格子的距离）即可。
最终，我们得到的题解代码为：

public int maxDistance(int[][] grid) {
    int N = grid.length;

    Queue<int[]> queue = new ArrayDeque<>();
    // 将所有的陆地格子加入队列
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            if (grid[i][j] == 1) {
                queue.add(new int[]{i, j});
            }
        }
    }

    // 如果地图上只有陆地或者海洋，返回 -1
    if (queue.isEmpty() || queue.size() == N * N) {
        return -1;
    }

    int[][] moves = {
        {-1, 0}, {1, 0}, {0, -1}, {0, 1},
    };

    int distance = -1; // 记录当前遍历的层数（距离）
    while (!queue.isEmpty()) {
        distance++;
        int n = queue.size();
        for (int i = 0; i < n; i++) { 
            int[] node = queue.poll();
            int r = node[0];
            int c = node[1];
            for (int[] move : moves) {
                int r2 = r + move[0];
                int c2 = c + move[1];
                if (inArea(grid, r2, c2) && grid[r2][c2] == 0) {
                    grid[r2][c2] = 2;
                    queue.add(new int[]{r2, c2});
                }
            }
        }
    }

    return distance;
}

// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
    return 0 <= r && r < grid.length 
        && 0 <= c && c < grid[0].length;
}

DFS简介

定义上的深度优先搜索的思路与树的先序遍历非常相似，是针对图的搜索而提出的一种算法，下面是算法导论上的解释：

在深度优先搜索中，对于最新发现的顶点，如果它还有以此为顶点而未探测到的边，就沿此边继续探测下去，当顶点v的所有边都已被探寻过后，搜索将回溯到发现顶点v有起始点的那些边。这一过程一直进行到已发现从源顶点可达的所有顶点为止。如果还存在未被发现的顶点，则选择其中一个作为源顶点，并重复上述过程。整个过程反复进行，直到所有的顶点都被发现时为止。

在深度优先搜索中，每当扫描到已发现的顶点u的邻接表，从而发现新顶点v时，就将置v的先辈域Π[v]为u。与广度优先搜索不同的是，其先辈子图形成一棵树，深度优先搜索产生的先辈子图可以有几棵树所构成，因为搜索可能由多个源顶点开始重复进行。因此，在深度优先搜索中，先辈子图的定义也和广度优先搜索中稍有所不同：GΠ = (V, EΠ)，其中EΠ = {(Π[v], v) : v ∈V 且 Π[v] ≠ NIL}

在实际的操作中，我们一般对深度优先搜索问题进行分类：

定义的DFS：对图的连通性进行测试，典型的问题：迷宫连通性测试、图的条件搜索等
广义的DFS–DFS思路的应用：DFS搜索顺序+规则问题、穷举结果寻求最优解/符合条件解等等，由于其穷举答案的本质，又被称为爆搜

深度优先搜索(下文统称DFS)的精髓在于递归求解问题的思路以及回溯的处理。而针对搜索的过程，又有更为重要的剪枝、优化，必要的剪枝优化(通过对穷举答案方式进行改进)对DFS的顺利执行有着不可或缺的作用。本文章将针对DFS的原理、常见的题型、剪枝优化的思路进行分析。当然，爆搜的题型千千万，不可能一概而论，我会通过具体的题目对几类问题的求解思路进行总结分析，构建基本的思维模型。

DFS原理分类与分析

1. DFS连通性模型

在测试图的连通性时，DFS与实际人们的思想一致，相对于起点选择一条路走到底，发现不行就返回选择的节点换一条路试，直到试出一条能到达终点的路。当然，一直试不出来就表示该起点与某点(终点)不连通。其他DFS连通性模型的思想与之类似。

针对实际问题，我又将连通性模型按照是否需要回溯继续细分：

无需回溯：统计某点能到达的点的个数问题
在这类问题中，我们一般从某点出发进行搜索，对于已经被搜索过的点可以直接抛弃(标记不可访问)，对于当前被搜索的点递归搜索周围邻接的点并进行计数，直到无法搜索到合法的点返回。最终计数变量将记录所有能到达的点。

典型模板题：ACWing.1113 红与黑
解题报告：https://blog.csdn.net/yanweiqi1754989931/article/details/109243556X

需要回溯：迷宫类问题，测试两点间连通性
在这类问题中，由于当前选择的路径未必能够到达目标点，因此需要设置回溯，当搜索到非法路径返回时需要“恢复现场”，即：对于该路径下各点的访问状态重置。具体的搜索过程如下图所演示：

在这里插入图片描述

典型模板题：ACWing.1112 迷宫
解题报告：https://blog.csdn.net/yanweiqi1754989931/article/details/109239579
二维矩阵里走迷宫，非常简单

典型模板题：ACWing.1116 马走日
解题报告：https://blog.csdn.net/yanweiqi1754989931/article/details/109247649
这题堪称经典，与迷宫模板不同的是移动路径的选择和点合法性的判断，属于简单的搜索题

根据数据结构，又可以将两个模型分别继续细分，DFS可以基于邻接矩阵、邻接表、边集数组实现，思路相同，只是路径的遍历方式、点的访问有所改变。

这里留个坑，以后会选择不同数据结构类型的题目补充在这里

总结一下DFS的模板框架(简单描述)

function dfs(当前状态){
	if(当前状态 == 目的状态){
        ···
    }
    for(···寻找新状态){
        if(状态合法){
            vis[访问该点]；
            dfs(新状态);
            ?是否需要恢复现场->vis[恢复访问]
        } 
    }
    if(找不到新状态){
        ···
    }
}

2. DFS思路应用-穷举求解问题

在无路可走时，我们往往会选择搜索算法，因为我们期望利用计算机的高性能来有目的的穷举一个问题的部分甚至所有可能情况，从而在这些情况中寻找符合题目要求的答案。这也是“爆搜”之名的由来

我们约定，对于问题的介入状态，叫初始状态，要求的状态叫目标状态。
这里的搜索就是对实时产生的状态进行分析检测，直到得到一个目标状态或符合要求的最佳状态为止。对于实时产生新的状态的过程叫扩展（由一个状态，应用规则，产生新状态的过程）

搜索的要点：

选定初始状态，在某些问题中可能是从多个合法状态分别入手搜索；
遍历自初始状态或当前状态所产生的合法状态，产生新的状态并进入递归；
检查新状态是否为目标状态，是则返回，否则继续遍历，重复2-3步骤

对状态的处理：DFS时，用一个数组存放产生的所有状态。

把初始状态放入数组中，设为当前状态；
扩展当前的状态，从合法状态中旬寻找一个新的状态放入数组中，同时把新产生的状态设为当前状态；
判断当前状态是否和前面的状态重复，如果重复则回到上一个状态，产生它的另一状态；
判断当前状态是否为目标状态，如果是目标目标状态，则找到一个解答，根据实际问题需求，选择继续寻找答案或是直接返回。
如果数组为空，说明对于该问题无解。

与图的搜索类似，算法的框架基本不变，不同的是对于新状态的寻找、控制递归终止的条件更为复杂。在实际的题目中，会有一些题目需要对合法的新状态进行干预：可能在首轮搜索无法应用规则或所有条件均不满足且需要人为创建新的规则以继续搜索答案。这里也会设计到一系列剪枝与优化的问题。

function dfs(当前状态, 一系列其他的状态量){
	if(当前状态 == 目的状态){
        ···
    }
    for(···寻找新状态){
        if(状态合法){
            vis[访问该点]；
            dfs(新状态);
            ?是否需要恢复现场->vis[恢复访问]
        } 
    }
    if(找不到新状态){
        是否需要创建新规则？{
            创建并对当前状态进行访问vis;
            继续搜索;
            恢复现场/恢复访问vis;
        }
    }
}