Problem - C - Codeforces

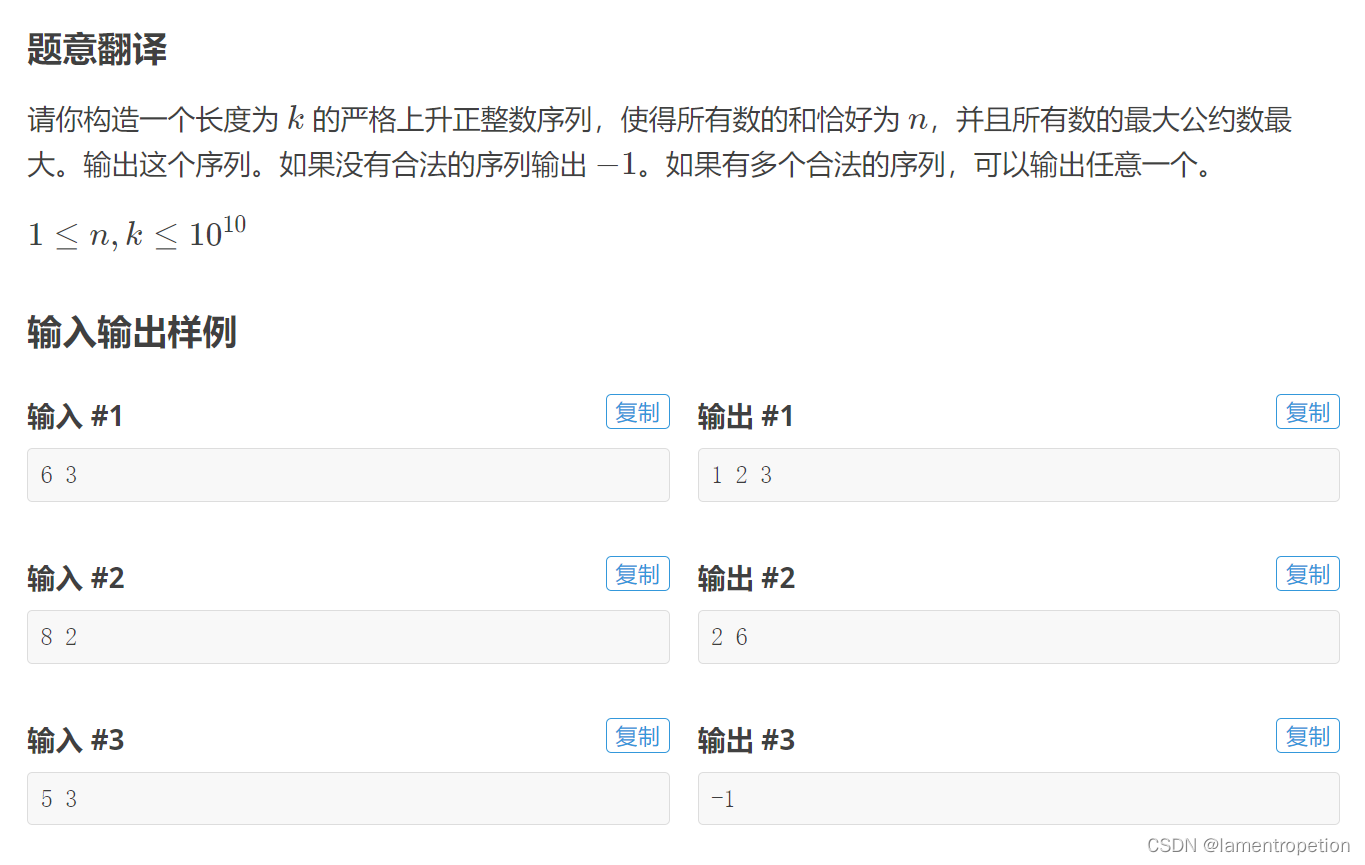
题意：

思路：

要使所有数的 gcd 尽可能大

设 gcd = k

那么就是 k1 * k，k2 * k，k3 * k，....

它们的和是n

那么(k1 + k2 + k3 +....) * k = n

根据惯用套路，我们去枚举 n 的因子即可

因为要求严格递增，贪心地考虑，构造成1，2，3，....，k - 1即可

然后最后一项就是 n - k * (k - 1) / 2

需要判断最后一项要大于k - 1

注意 gcd = 1和 gcd = n的情况要特判，不然枚举因子的时候会超时

还有就是，(2 * n) / k < 1 + k) 的情况直接判无解，否则会超时

Code：

#include <bits/stdc++.h>

using i64 = long long;

const int N = 2e5 + 10;

i64 n, k;

void solve() {
    std::cin >> n >> k;

    if((2 * n) / k < 1 + k) {
		std::cout << -1 << "\n";
		return;
	}
    std::vector<int> V;
    for (int i = 2; i <= n / i ; i ++) {
        if (n % i == 0) {
            V.push_back(i);
            if (i != n / i) V.push_back(n / i);
        }
    }
    
    std::sort(V.begin(), V.end());

    bool ok = false;
    //特判gcd == n
    if (k == 1) {
        ok = true;
        std::cout << n << "\n";
        return;
    }
    //gcd在1到n之间
    for (int i = V.size() - 1; i >= 0; i --) {
        int d = V[i];
        int sum = n / d;
        if (sum - k * (k - 1) / 2 <= k - 1) continue;
        ok = true;
        for (int i = 1; i <= k - 1; i ++) {
            std::cout << i * d << " "; 
        }
        std::cout << ((n / d) - (k * (k - 1) / 2)) * d << "\n";
        break;
    }

    //特判gcd == 1
    if ((n - k * (k - 1) / 2) > k - 1 && ok == false) {
        ok = true;
        for (int i = 1; i <= k - 1; i ++) std::cout << i << " ";
        std::cout << n - k * (k - 1) / 2 << "\n";
    }
    if (ok == false) {
        std::cout << -1 << "\n";
    }
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t = 1;
    
    while (t--) {
        solve();
    }
    
    return 0;
}